Minimum accelerator energy to run experiment

Go Back

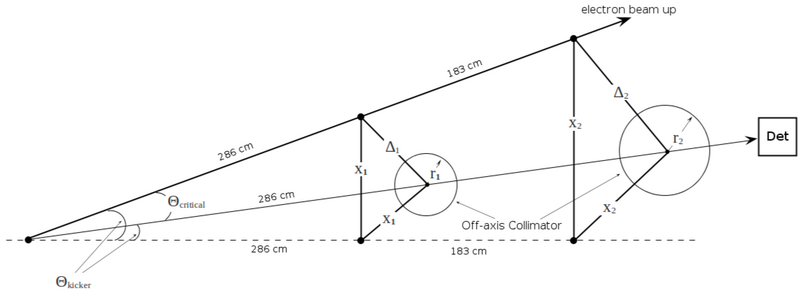
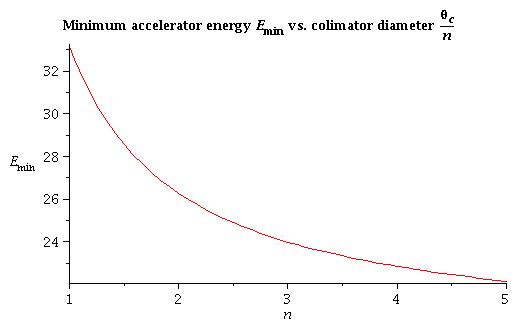
condition 1: fitting the collimator size into the hole

The minimum energy of accelerator (MeV) is limited by fitting the collimator size [math]r_2[/math] into the hole R = 8.73 cm:

[math]x_2 + r_2 = R[/math]

1) Assuming the collimator diameter is [math]\Theta_C[/math]:

[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
       \frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV  [/math]

2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:

[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
       \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV  [/math]

3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:

[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
       \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV  [/math]

4) for arbitrary collimator size [math]\Theta_C/2[/math]:

All energy under this line is good to run experiment for condition above

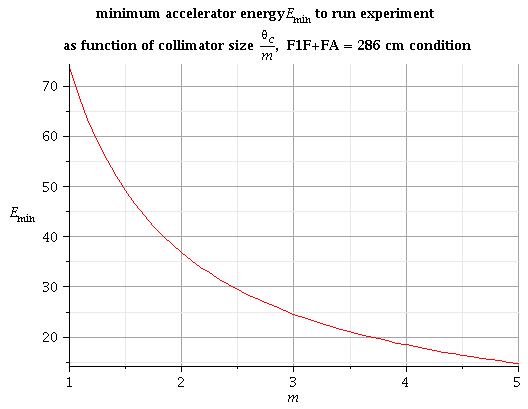
condition 2: F1A = 286 cm

1) assuming the collimator diameter is [math]\Theta_C[/math]

[math] E_{min} = 73.7\ MeV  [/math]

2) assuming the collimator diameter is [math]\Theta_C/2[/math]

[math] E_{min} = 36.9\ MeV  [/math]

3) assuming the collimator diameter is [math]\Theta_C/4[/math]

[math] E_{min} = 18.4\ MeV  [/math]

4) for arbitrary collimator size [math]\Theta_C/m[/math]:

All energy above this line is good to run experiment

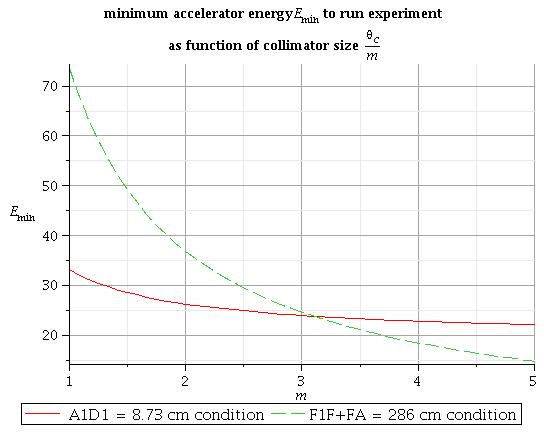
both conditions above are together

All energy above this lines is good to run experiment

Go Back