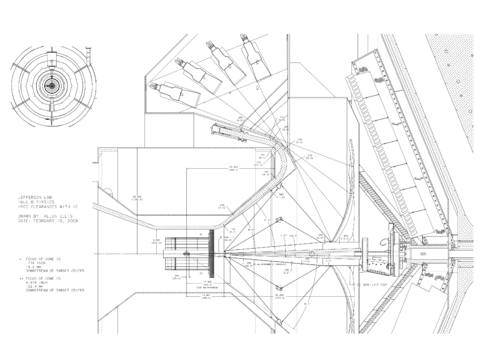
Lead Shield Cone

Target

We need to edit the EXn02DetectorConstruction file to allow for a target that is a lead cone to simulate the Moller Shield. The header file for an elliptical Cone gives the parameters need to call with.

// $Id: G4EllipticalCone.hh 67011 2013-01-29 16:17:41Z gcosmo $
//  
//    
// --------------------------------------------------------------------
// GEANT 4 class header file
//   
// G4EllipticalCone
// 
// Class description:
//
// G4EllipticalCone is a full cone with elliptical base which can be cut in Z.
//
// Member Data:
//
//      xSemiAxis       semi-axis, x, without dimentions
//      ySemiAxis       semi-axis, y, without dimentions
//      zheight         height, z
//      zTopCut         upper cut plane level, z
// 
// The height in Z corresponds to where the elliptical cone hits the
// Z-axis if it had no Z cut. Also the cone is centered at zero having a
// base at zTopCut and another at -zTopCut. The semi-major axes at the Z=0
// plane are given by xSemiAxis*zheight and ySemiAxis*zheight so that the
// curved surface of our cone satisfies the equation:
// 
// ***************************************************************************
// *                                                                         *
// *           (x/xSemiAxis)^2 + (y/ySemiAxis)^2 = (zheight - z)^2           *
// *                                                                         *
// ***************************************************************************
// 
// In case you want to construct G4EllipticalCone from :
//   1. halflength in Z = zTopCut
//   2. Dx and Dy =  halflength of ellipse axis  at  z = -zTopCut
//   3. dx and dy =  halflength of ellipse axis  at  z =  zTopCut
//      ! Attention :  dx/dy=Dx/Dy
// 
// You need to find xSemiAxis,ySemiAxis and zheight:
//
//  xSemiAxis = (Dx-dx)/(2*zTopCut)
//  ySemiAxis = (Dy-dy)/(2*zTopCut)
//    zheight = (Dx+dx)/(2*xSemiAxis)

The geometry looks like

Solving the variables:

1. halflength in Z = zTopCut

The cone shape starts 380 cm from the vertex point of (0,0,0). It extends 1325.9 beyond the starting position. This gives the z(max) as z = 1705.9 cm. Since this cone is centered at the vertex with zTopCut positive and negative placed an equal distance from the vertex, 1325.9/2=662.95 cm

2. Dx and Dy = halflength of ellipse axis at z = -zTopCut

The length of the x and y components at the smaller end of the cone are found from the diameter at this position. Assuming a circle for the cross-cut, then x=y=0.5 dia= 43 cm /2 = 21.5 cm

3. dx and dy = halflength of ellipse axis at z = zTopCut

Using geometry, for a right triangle with it's apex at the vertex and a height of 1705.9, with an interior angle of 5 degrees.

[math]1705.9\ cm\ Tan\ 5^\circ=149.247\ cm[/math]

Solving for the variable to pass to the function:

[math] xSemiAxis = \frac{Dx-dx}{2*zTopCut}= \frac{21.5-149.247}{2*662.95}= \frac{-127.747}{1325.9}=-0.096=ySemiAxis [/math]

The height in z is defined at the the point where the cone vertex crosses the z=0 plane in x&y. From the drawing, the vertex is originally placed at 0,0,0. Since the GEANT4 cone is centered at a new vertex with the circular cross sections of the cone at +/- 662.95, and the distance from the first smaller cross section is 380, this gives the intersection at -1042.95 cm with respect to the new vertex.

[math]zheight = \frac{Dx+dx}{2*xSemiAxis}=\frac{21.5+149.247}{2*-0.096}=\frac{170.747}{-0.192}=-889.307[/math]