Se170063 Thin Window Analysis

From New IAC Wiki
Jump to navigation Jump to search

In order to try to pin down the ratio of pure selenium to the selenium in the soil, try using a 2 channel window to find the signal. The error in the signal will be found by integrating the fit gaussian function over the window and "widening" it by half its standard deviation. Since the max value is fixed, it does not appear in the stats box, but I have included it in the table. It would seem that widening the gaussian function by half of its standard deviation yields results that agree up to 3 digits after the decimal with the result of widening the gaussian by its standard deviation. This would imply not much has changed between these methods.


400 <t< 640 sec 1100 < t < 1360 sec 1875 < t < 2150 2650 < t < 2930 sec 3400 < t < 3690 sec 4120 < t < 4400 sec 4840 < t < 5130 sec
Thin Window 170063 PureSe ThinWindow 400 640Sec.png 170063 PureSe 1100 1360Sec ThinWindow.png 170063 PureSeSpec 1875 2150Sec ThinWindow.png 170063 PureSeSpec 2650 2930Sec ThinWindow.png 170063 PureSeSpec 3400 3690Sec ThinWindow.png 170063 PureSeSpec 4120 4400Sec ThinWindow.png 170063 PureSeSpec 4840 5130Sec ThinWindow.png
Original Window 170063 PureSe 400 640Sec OGWindow.png 170063 PureSe 1100 1360 Seconds OGWindow.png 170063 PureSeSpec 1875 2150Sec OGWindow.png 170063 PureSeSpec 2650 2930Sec OGWindow.png 170063 PureSeSpec 3400 3690Sec OGWindow.png 170063 PureSeSpec 4120 4400Sec OGWindow.png 170063 PureSeSpec 4840 5130 OGWindow.png
Expanded Window 170063 PureSe 400 640Sec ExpWindow.png 170063 PureSeSpectrum 1100 1360Sec ExpWindow.png 170063 PureSeSpec 1875 2150 ExpWindow.png 170063 PureSeSpec 2650 2930Sec ExpWindow.png 170063 PureSeSpec 3400 3690Sec ExpWindow.png 170063 PureSeSpec 4120 4400Sec ExpWindow.png 170063 PureSeSpec 4840 5130Sec ExpWindow.png
Maximum of Histogram 260980 241756 220348 191476 165549 139528 130930
Original Background 10560 +/- 51.58 10560 +/- 51.41 9496 +/- 48.9 8898 +/- 47.1 9418 +/- 48.2 7485 +/- 43 7032 +/- 31.1
Expanded Background 10750 +/- 42.42 10630 +/- 42.09 9674 +/- 40.2 9029 +/- 38.7 9248 +/- 39.1 7634 +/- 35.5 7161 +/- 34.2
Signal Background (Take Larger Error) 10560 +/- 51.58 10560 +/- 51.41 9496 +/- 48.9 8898 +/- 47.1 9418 +/- 48.2 7485 +/- 43 7161 +/- 34.2
Integrated Background 21120 +/- 103.16 21120 +/- 102.82 18992 +/- 97.8 17796 +/- 94.2 18836 +/- 96.4 14970 +/- 86 14322 +/- 68.4
Signal in Thin Window 466700 +/- 100640 444100 +/- 107283 412800 +/- 105315 356800 +/- 90071 304100 +/- 70533 258700 +/- 63093 233500 +/- 52318
Background Subtracted Signal 445580 +/- 100640 422980 +/- 107283 393808 +/- 105315 339004 +/- 90071 285264 +/- 70533 243730 +/- 63093 219178 +/- 52318
Time Correction Factor (Sec) 400 370 395 400 350 345 360
Corrected Counts 483015.53 +/- 109095.5248 455750 +/- 115595.0622 426463.63 +/- 114048.1804 367485.52 +/- 97638.49218 306127.92 +/- 75691.81615 261292.55 +/- 67639.40782 235683.31 +/- 56257.91145
.dat file entry 7.607165162 +/- 0.2258633895 7.469018062 +/- 0.2536369988 7.346511269 +/- 0.2676838585 7.179649592 +/- 0.2656934406 6.96187741 +/- 0.2472555138 6.838606337 +/- 0.2588646627 6.700363353 +/- 0.2387012956

Below is the table for the Se-Ash Mixture


0 <t< 300 sec 730 < t < 1020 sec 1480 < t < 1775 2250 < t < 2550 sec 3050< t < 3300 sec 3775 < t < 4050 sec 4480 < t < 4770 sec
Thin Window 170063 MixSpec 0 300Sec ThinWindow.png 170063 MixSpec 730 1020Sec ThinWindow.png 170063 MixSpec 1480 1775Sec ThinWindow.png 170063 MixSpec 2250 2550Sec ThinWindow.png 170063 MixSpec 3050 3300Sec ThinWindow.png 170063 MixSpec 3775 4050Sec ThinWindow.png 170063 MixSpec 4480 4770Sec ThinWindow.png
Original Window 170063 MixSpec 0 300 OGWindow.png 170063 MixSpec 730 1020Sec OGWindow.png 170063 MixSpec 1480 1775Sec OGWindow.png 170063 MixSpec 2250 2550Sec OGWindow.png 170063 MixSpec 3050 3300Sec OGWindow.png 170063 MixSpec 3775 4050Sec OGWindow.png 170063 MixSpec 4480 4770Sec OGWindow.png
Expanded Window 170063 MixSpec 0 300Sec ExpWindow.png 170063 MixSpec 730 1020Sec ExpWindow.png 170063 MixSpec 1480 1775Sec ExpWindow.png 170063 MixSpec 2250 2550Sec ExpWindow.png 170063 MixSpec 3050 3300Sec ExpWindow.png 170063 MixSpec 3775 4050Sec ExpWindow.png 170063 MixSpec 4480 4770Sec ExpWindow.png
Maximum of Histogram 173289 155770 135740 124656 88582 80993 77781
Original Background 29440 +/- 84.93 20580 +/- 70.31 16420 +/- 62.52 14460 +/- 58.47 10950 +/- 50.65 10530 +/- 49.90 9809 +/- 48.2
Expanded Background 28960 +/- 69.12 20580 +/- 57.79 16500 +/- 51.60 14500 +/- 48.2 10630 +/- 41.29 10460 +/- 41.01 9814 +/- 39.7
Signal Background (Take Larger Error) 29440 +/- 84.93 20580 +/- 70.31 16420 +/- 62.52 14460 +/- 58.47 10950 +/- 50.65 10530 +/- 49.90 9809 +/- 48.2
Integrated Background 58880 +/- 169.86 41160 +/- 140.62 32840 +/- 131.04 28920 +/- 116.94 21900 +/- 101.3 21060 +/- 99.8 19618 +/- 96.4
Signal in Thin Window 342200 +/- 92880 300100 +/- 78390 267200 +/- 74626 238600 +/- 63463 170100 +/- 46436 153200 +/- 39780 147900 +/- 38766
Background Subtracted Signal 283320 +/- 92880 258940 +/- 78390 234360 +/- 74626 209680 +/- 63463 148200 +/- 46436.11 132140 +/- 39780.13 128282 +/- 37866.12
.dat file entry 6.850549805 +/- 0.3278271919 6.794470731 +/- 0.3027342241 6.677638317 +/- 0.3181179382 6.549555363 +/- 0.3026659672 6.384857074 +/- 0.3184246458 6.174846148 +/- 0.3010453307 6.092105322 +/- 0.2951787468


Below is a plot of the ratio of the activities where the pure selenium sample has been time corrected back to match the run time of the mixture.

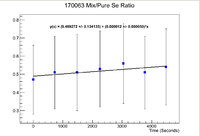
170063 MixVsPureRatio ThinWindowMethod.png

Note that this does give the expected result that the ratio between the two samples is statistically the same as 0.5, which is the ratio of the masses. The only problem here is that the error is quite large, The average of the uncertainty divided by the mean is 39.6%.

Below are the half life plots for the Pure Selenium sample and the ash mixture


170063 MixHLPlot ThinWindowMethod.png

170063 PureSeHLPlot ThinWindowMethod.png


The slope of the mixture plot gives a half life of 63.48 +/- 26.85 minutes. This does overlap, but the error is extremely large.

The slope of the pure selenium sample plot gives a half life of 56.08 +/- 16.33 minutes. Again this does overlap, but the error is still quite large.

The ratio of the initial activities is 0.49 +/- 0.13. Now this does fall within 1 standard deviation of 0.5, which is the value we want.


Dead Time Corrected

I have shown that by tracing the activity back in time for the pure selenium sample that the activities are the same here LB Thesis Thin Window Analysis, but now I must make sure that this will actually give the ratio that is expected.

Begin with the third measurement that was taken for the pure selenium sample


Third Pure Se Measurement

Below is the histogram of interest

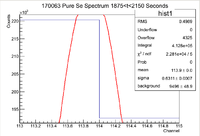
170063 PureSeSpec 1875 2150Sec ThinWindow.png

From this we can see that

[math] I \pm \sigma_I = 412800 \pm 642.50 Counts [/math]

and the integrated background is given by

[math] B \pm \sigma_B = 18992 \pm 97.8 Counts[/math]

Now we can find the background subtracted signal

[math] N \pm \sigma_N = 393808 \pm 649.90 Counts[/math]

Now convert this into an activity by dividing by the runtime

[math] A_{Measure} \pm \sigma_{A_{Measure}} = \frac{393808}{275} \pm \frac{649.90}{275} = 1432.03 \pm 2.36 Hz [/math]

Now we can find the true value using the integrated measurement

[math] A_{True} \pm \sigma_{A_{True}} = \frac{e^{\lambda \times 275} \times 1432.03 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 1472.11 Hz [/math]

[math] \sigma_{A_{True}} = \frac{e^{\lambda \times 275} \times 2.36 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 2.43 Hz [/math]

So now the true value for the activity is

[math] A_{True} \pm \sigma_{A_{True}} = 1472.11 \pm 2.43 Hz [/math]

Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.3

[math] A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 1472.11 \times \frac{1}{0.9747} = 1510.32 Hz [/math]

[math] \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 [/math]

[math] \sigma_{A_{True}^{DT}} = \sqrt{DTC^2 \times \sigma_{A}^2 + A^2 \times \sigma_{DTC}^2} = \sqrt{1.03^2 \times 2.43^2 + 1472.11^2 \times 0.003^2} = 5.08 Hz [/math]

So the real activity for the third measurement of the Pure Se sample is

[math] A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1510.32 \pm 5.08 [/math]

Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion)


Fourth Pure Se Measurement

Now do the analysis for the 4th measurement taken on the pure selenium sample.

Below is the histogram of interest

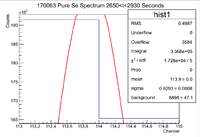
170063 PureSeSpec 2650 2930Sec ThinWindow.png

From this we can see that

[math] I \pm \sigma_I = 356800 \pm 597.33 Counts [/math]

and the integrated background is given by

[math] B \pm \sigma_B = 17796 \pm 94.2 Counts[/math]

Now we can find the background subtracted signal

[math] N \pm \sigma_N = 339004 \pm 604.71 Counts[/math]

Now convert this into an activity by dividing by the runtime

[math] A_{Measure} \pm \sigma_{A_{Measure}} = \frac{339004}{280} \pm \frac{604.71}{280} = 1210.73 \pm 2.16 Hz [/math]

Now we can find the true value using the integrated measurement

[math] A_{True} \pm \sigma_{A_{True}} = \frac{e^{\lambda \times 280} \times 1210.73 \times 280 \times \lambda}{e^{\lambda \times 280}-1} =1245.24 Hz [/math]

[math] \sigma_{A_{True}} = \frac{e^{\lambda \times 280} \times 2.16 \times 280 \times \lambda}{e^{\lambda \times 280}-1} = 2.22 Hz [/math]

So now the true value for the activity is

[math] A_{True} \pm \sigma_{A_{True}} = 1245.24 \pm 2.22 Hz [/math]

Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.3

[math] A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 1472.11 \times \frac{1}{0.9747} = 1510.32 Hz [/math]

[math] \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 [/math]

[math] \sigma_{A_{True}^{DT}} = \sqrt{DTC^2 \times \sigma_{A}^2 + A^2 \times \sigma_{DTC}^2} = \sqrt{1.03^2 \times 2.43^2 + 1472.11^2 \times 0.003^2} = 5.08 Hz [/math]

So the real activity for the third measurement of the Pure Se sample is

[math] A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1510.32 \pm 5.08 [/math]


400 <t< 640 sec 1100 < t < 1360 sec 1875 < t < 2150 2650 < t < 2930 sec 3400 < t < 3690 sec 4120 < t < 4400 sec 4840 < t < 5130 sec
.dat file entry 7.58 +/- 0.003 7.45 +/- 0.003 7.32 +/- 0/003
Retrieved from "https://wiki.iac.isu.edu/index.php?title=Se170063_Thin_Window_Analysis&oldid=119867"