Limits based on Mandelstam Variables
s Channel
[math]s \equiv \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=\left({\mathbf P_1^{'*}}+ {\mathbf P_2^{'*}}\right)^2[/math]
In the center of mass frame, the momentum of the particles interacting are equal and opposite, i.e. [math]p_1^*=-p_2^*[/math]. However, the 4-momentum still retains an energy component, which as a scalar quantity, can not be countered by another particle's direction of motion.
[math]s \equiv \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2[/math]
[math]s \equiv P_1^{*2}+2P_1^*P_2^*+P_2^{*2}[/math]
Similarly, by the relativistic definition of energy
[math]E^2 \equiv p^2+m^2[/math]
where both particles have the same mass, this implies
[math] \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=4E_{CM}^2=4(m_{CM}^2+p_{CM}^2)=s[/math]
[math]s=4(m_{CM}^2+p_{CM}^2)[/math]
t Channel
[math]t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2[/math]
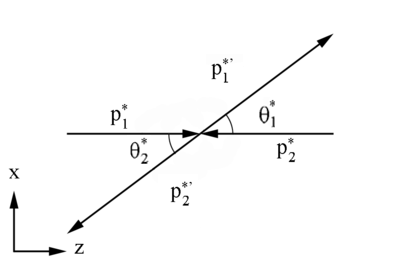
[math]t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2[/math]
[math]t \equiv P_1^{*2}-2P_1^*P_1^{'*}+P_1^{'*2}[/math]
[math]t \equiv 2m_1^2-2E_1^*E_1^{'*}+2p_1^*p_1^{'*}[/math]
[math]t \equiv 2m_1^*-2E_1^{*2}+2p_1^{*2}cos\ \theta[/math]
[math]t \equiv -2p_1^{*2}(1-cos\ \theta)[/math]
u Channel
