[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Relativistic Frames of Reference
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that
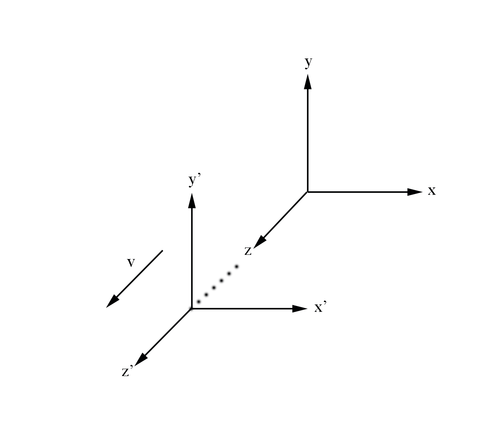
Figure 2.1: Primed reference frame moving in the z direction with velocity v.
[math]t= t'[/math]
[math]x=x'[/math]
[math]y=y'[/math]
[math]z=z'+vt[/math]
Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:
[math]speed=\frac{\Delta Distance}{\Delta Time}[/math]
[math]c=\frac{\Delta d}{\Delta t}[/math]
where
[math]c=3\times 10^8\ m/s[/math]
Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes
[math]c=\frac{\sqrt{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}}{\Delta t}[/math]
Following the postulate of Special Relativity, this implies for the primed frame
[math]c=\frac{\sqrt{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}}{\Delta t'}[/math]
We can rewrite this as
[math]\frac{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}{(\Delta t')^2}= c^2=\frac{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}{(\Delta t)^2}[/math]
This is possible since the ratios of distance to time are multiples of the same base, i.e. [math]\frac{3\times 10^8\ m}{s}[/math]
[math]c^2 \Delta t^{'2}=(\Delta x')^2+(\Delta y')^2+(\Delta z')^2\ \ \ \ \ c^2 \Delta t^{2}=(\Delta x)^2+(\Delta y)^2+(\Delta z)^2[/math]
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
