Plotting Different Frames

From New IAC Wiki
Revision as of 18:58, 1 May 2017 by Vanwdani (talk | contribs)
Jump to navigation Jump to search

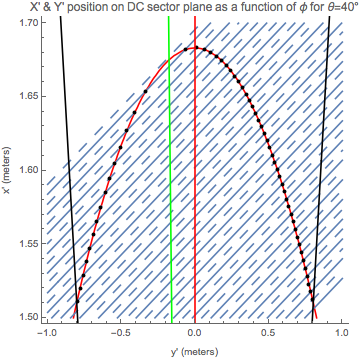
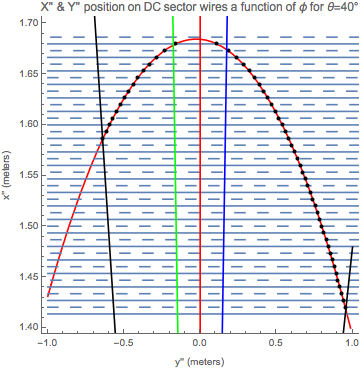
We can define different arrays to collect the coordinates in the different frames using a passive transformation. Assuming that the intersection of the ellipse and sense wires is in the y-x plane, we will have a positive rotation, [math]R(\theta_{yx})[/math] 


rFromYtoX = ( {
    {Cos[6 \[Degree]], -Sin[6 \[Degree]], 0},
    {Sin[6 \[Degree]], Cos[6 \[Degree]], 0},
    {0, 0, 1}
   } );
rFromXtoY = ( {
    {Cos[6 \[Degree]], Sin[6 \[Degree]], 0},
    {-Sin[6 \[Degree]], Cos[6 \[Degree]], 0},
    {0, 0, 1}
   } );
yxPoints = constant\[Theta];
constant\[Theta]yx = constant\[Theta];
constant\[Theta]yxRotated = constant\[Theta];
constant\[Theta]xyz = constant\[Theta];
constant\[Theta]xyzRotated = constant\[Theta];

RowLengths = Table[{Nothing}, {i, 1, 36}];
For[rows = 1, rows < 37, rows++,
  RowLengths[[rows]] = Length[constant\[Theta][[rows]]];
  For[columns = 1, columns < RowLengths[[rows]] + 1, columns++,
   \[Theta] = rows + 4;
   \[Phi] = constant\[Theta][[rows, columns, 1]];
   constant\[Theta]yx[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a};
   constant\[Theta]xyz[[rows, 
     columns]] = {constant\[Theta]yx[[rows, columns, 2]], 
     constant\[Theta]yx[[rows, columns, 1]], 0};
   If[constant\[Theta][[rows, columns, 1]] < 0,
    constant\[Theta]yx[[rows, columns, 
      1]] = -constant\[Theta]yx[[rows, columns, 1]];
    constant\[Theta]xyz[[rows, columns, 
      2]] = -constant\[Theta]xyz[[rows, columns, 2]];
    ];
   constant\[Theta]xyzRotated[[rows, columns]] = 
    rFromYtoX.{constant\[Theta]xyz[[rows, columns, 1]], 
      constant\[Theta]xyz[[rows, columns, 2]], 
      constant\[Theta]xyz[[rows, columns, 3]]};
   
   constant\[Theta]yxRotated[[rows, 
     columns]] = {constant\[Theta]xyzRotated[[rows, columns, 2]], 
     constant\[Theta]xyzRotated[[rows, columns, 1]]};
   yxPoints[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a, 
     constant\[Theta][[rows, columns, 1]], 
     constant\[Theta][[rows, columns, 2]]};
   
   ]
  ];
ClearAll[\[Theta], \[Phi]];
DesiredyxPoints = Desiredconstant\[Theta];
Desiredconstant\[Theta]yx = Desiredconstant\[Theta];
Desiredconstant\[Theta]yxRotated = Desiredconstant\[Theta];
Desiredconstant\[Theta]xyz = Desiredconstant\[Theta];
Desiredconstant\[Theta]xyzRotated = Desiredconstant\[Theta];

DesiredRowLengths = Table[{Nothing}, {i, 1, 36}];
For[rows = 1, rows < 37, rows++,
  DesiredRowLengths[[rows]] = 
   Length[Desiredconstant\[Theta][[rows]]];
  For[columns = 1, columns < DesiredRowLengths[[rows]] + 1, 
   columns++,
   \[Theta] = rows + 4;
   \[Phi] = Desiredconstant\[Theta][[rows, columns, 1]];
   Desiredconstant\[Theta]yx[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a};
   Desiredconstant\[Theta]xyz[[rows, 
      columns]] = {Desiredconstant\[Theta]yx[[rows, columns, 2]], 
     Desiredconstant\[Theta]yx[[rows, columns, 1]], 0};
   If[Desiredconstant\[Theta][[rows, columns, 1]] < 0,
    Desiredconstant\[Theta]yx[[rows, columns, 
       1]] = -Desiredconstant\[Theta]yx[[rows, columns, 1]];
    Desiredconstant\[Theta]xyz[[rows, columns, 
       2]] = -Desiredconstant\[Theta]xyz[[rows, columns, 2]];
    ];
   Desiredconstant\[Theta]xyzRotated[[rows, columns]] = 
    rFromYtoX.{Desiredconstant\[Theta]xyz[[rows, columns, 1]], 
      Desiredconstant\[Theta]xyz[[rows, columns, 2]], 
      Desiredconstant\[Theta]xyz[[rows, columns, 3]]};
   
   Desiredconstant\[Theta]yxRotated[[rows, 
      columns]] = {Desiredconstant\[Theta]xyzRotated[[rows, columns, 
       2]], Desiredconstant\[Theta]xyzRotated[[rows, columns, 1]]};
   DesiredyxPoints[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a, 
     Desiredconstant\[Theta][[rows, columns, 1]], 
     Desiredconstant\[Theta][[rows, columns, 2]]};
   
   ]
  ];
ClearAll[\[Theta], \[Phi]]


The parameter's range changes from the DC frame with 0<t<2[math]\pi[/math], since

[math]x(t=0)=a\ cos\ t = a\ cos\ 0 =a = a\ cos\ 2 \pi =x(t=2 \pi)[/math]


[math]y(t=0)=b\ sin\ t = b\ sin\ 0 = 0 = b\ sin\ 2 \pi = y(t=2 \pi)[/math]

In the frame of the wires, the x axis no longer is aligned with the semi-major axis, therefore for [math]\theta=40^{\circ}, \phi=0, t=0 [/math] in the DC frame 


In[153]:= ClearAll[X, \[Theta]];
\[Theta] = 40;
X = X /. Solve[(X + \[CapitalDelta]a)^2/a^2 == 1 && X > 0, X]

Out[155]= {1.68318}

This gives the (x' , y')=(1.68318, 0) in the DC frame for[math] \phi=0^{\circ}, t=0[/math] 


In[162]:= rFromXtoY.{1.6831832367824053`, 0, 0} // MatrixForm

Out[162]//MatrixForm= \!\(
TagBox[
RowBox[{"(", "", 
TagBox[GridBox[{
{"1.6739625828969429`"},
{
RowBox[{"-", "0.17594055713873974`"}]},
{"0.`"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.5599999999999999]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}}],
Column], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)


The slope m, with respect to x, is found as [math]\frac{\Delta\ x}{\Delta\ y} = \frac{1.67396 - 1.076}{-0.175941 + 0.113092}=\frac{0.59796}{-0.0628481}=-9.514[/math]


Slope point form gives

[math]x' - x_1=m(y'-y_1) [/math]


[math]\Rightarrow x' - 1.67396 = -9.514(y' + 0.17594) [/math]


[math]\Rightarrow y' = 9.514x'-1.67396 + 1.67396[/math]


[math]\Rightarrow y' = -9.514x'[/math]



SemiMajorAxisRotatedReverse = 
  ContourPlot[X == -9.514 Y, {Y, -2, 2}, {X, 0, 1.8}, 
   Frame -> {True, True, False, False}, 
       PlotLabel -> 
    "Right side limit of DC as a function of X and Y", 
   FrameLabel -> {"y (meters)", "x (meters)"}, 
   ContourStyle -> Green, 
       PlotLegends -> Automatic];

Graphing the frame of the sector and the wires within the sector, 


DataXY = Table[
   ListPlot[{constant\[Theta]yx[[i]]}, PlotStyle -> Black, 
    AxesLabel -> {"y", "x"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"], {i, 1, 
    36}];
DataXYRotated = 
  Table[ListPlot[{constant\[Theta]yxRotated[[i]]}, PlotStyle -> Black,
     AxesLabel -> {"y'", "x'"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"],
   {i, 1, 36}];
DesiredDataXY = 
  Table[ListPlot[{Desiredconstant\[Theta]yx[[i]]}, PlotStyle -> Black,
     AxesLabel -> {"y", "x"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"], {i, 1, 
    36}];
DesiredDataXYRotated = 
  Table[ListPlot[{Desiredconstant\[Theta]yxRotated[[i]]}, 
    PlotStyle -> Black, AxesLabel -> {"y'", "x'"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"],
   {i, 1, 36}];
ClearAll[\[Theta]];
\[Theta] = 40;
ellipse40 = 
  ContourPlot[(x + \[CapitalDelta]a)^2/a^2 + y^2/b^2 == 1, {y, -1, 
    1}, {x, 1.5, 1.7}, Frame -> {True, True, False, False}, 
   PlotLabel -> 
    "X' & Y' position on DC sector plane as a function of \[Phi] for \
\[Theta]=40\[Degree]", FrameLabel -> {"y' (meters)", "x' (meters)"}, 
   ContourStyle -> Red, PlotLegends -> Automatic];
ellipse40Rotated = 
  ContourPlot[(X Cos[6 \[Degree]] + 
       Y Sin[6 \[Degree]] + \[CapitalDelta]a)^2/
     a^2 + (-X Sin[6 \[Degree]] + Y Cos[6 \[Degree]])^2/b^2 == 
    1, {Y, -1, 1}, {X, 1.4, 1.7}, Frame -> {True, True, False, False},
    PlotLabel -> 
    "X'' & Y'' position on DC sector wires a function of \[Phi] for \
\[Theta]=40\[Degree]", FrameLabel -> {"y'' (meters)", "x'' (meters)"},
    ContourStyle -> Red, PlotLegends -> Automatic];
Show[ellipse40, 
 Table[ContourPlot[
   xWire == Tan[6 \[Degree]] yWire + x0forWires[number], {yWire, -1, 
    1}, {xWire, 1.5, 1.7}, 
   FrameLabel -> {"y(meters)", "x(meters)"}], {number, 89, 109}], 
 Table[ContourPlot[
   xWire == 
    Tan[6 \[Degree]] yWire + x0forWireMiddles[number2], {yWire, -1, 
    1}, {xWire, 1.5, 1.7},
   ContourStyle -> {Dashing[Large]}], {number2, 89, 109}], 
 DataXY[[36]], 
 DesiredDataXY[[36]], left, right, SemiMajorAxis, \
SemiMajorAxisRotatedReverse]
Show[ellipse40Rotated, 
 Table[ContourPlot[
   xWire == Cos[6 \[Degree]] x0forWires[number], {yWire, -1, 
    1.2}, {xWire, 1.4, 1.7}, 
   FrameLabel -> {"y(meters)", "x(meters)"}], {number, 89, 109}], 
 Table[ContourPlot[
   xWire == Cos[6 \[Degree]] x0forWireMiddles[number2], {yWire, -1, 
    1.2}, {xWire, 1.4, 1.7},
   ContourStyle -> {Dashing[Large]}], {number2, 89, 109}], 
 DataXYRotated[[36]], 
 DesiredDataXYRotated[[36]], rightRotated, leftRotated, \
SemiMajorAxisRotated, SemiMajorAxis, SemiMajorAxisRotatedReverse]
ClearAll[\[Theta]];


X'y'plane.png


X2y2plane.png
Retrieved from "https://wiki.iac.isu.edu/index.php?title=Plotting_Different_Frames&oldid=114083"