Determining wire-phi correspondance

Test for $\theta=20$ and $\phi=1$

All previous quantities where calculated for $\theta=20^{\circ}$ and do not depend on the angle $\phi$. The quantities that do change

$x_{D1}=r_{D1}\ cos(\phi)=.5901cos(1^{\circ}))=.5900\text {m}\qquad y_{D1}=r_{D1}cos(\phi)=.5901 sin(1^{\circ}))=.0103\qquad z_{D1}=r_{D1} cot(\theta)=.5901cot(20)=1.6212\ \text{m}$

$x_{D2}=r_{D2} cos(\phi)=1.3055cos(1^{\circ}))=1.3053\text {m}\qquad y_{D2}=r_{D2} sin(\phi)=1.3055sin(1^{\circ}))=.0228\qquad z_{D2}=r_{D2} cot(\theta)=1.3055cot(20)=3.5868\ \text{m}$

$x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53cos(1^{\circ}))}{(cot(20^{\circ})+cos(1^{\circ}))cot(65^{\circ})}=0.7869$

$y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53sin(1^{\circ}))}{(cot(20^{\circ})+cos(1^{\circ}))cot(65^{\circ})}=.0137$

$z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53cot(20^{\circ})}{(cot(20^{\circ})+cos(1^{\circ}))cot(65^{\circ})}=2.1624$

$D2P=\sqrt{(x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2}=\sqrt{(1.3053-0.7869)^2+(.0228-.0137)^2+(3.5868-2.1624)^2}=\sqrt{(.5184)^2+(.0091)^2+(1.4244)^2}=1.51582872713\ \text{m}$

$D1P=\sqrt{(x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2}=\sqrt{(0.7871-.5900)^2+(.0137-.0103)^2+(2.1624-1.6212)^2}=\sqrt{(.1971)^2+(.0034)^2+(.5412)^2}=.575983862621\ \text{m}$

$x_1^'=\frac{r_2^{'2}-r_1^{'2}}{4ae}-ae=\frac{1.5158^{'2}-.5758^{'2}}{4(1.0459)(.4497)}-(1.0459)(.4497)=.575\ \text{m}$

Using the pythagorean theorem

$y'=\sqrt{.576^2-.575^2}=.03\ \text{m}$

The two possible answers denote shifting to the left on right on the y axis. We take the direction of positive and negative to be the same as the sign convention for the angle phi starting on the x axis and shifting positive clockwise. A shift of 1 degree in phi at theta equal to 20 degrees only results in a small change in the x and y. This changes depending on the angles.

Function for the change in x' in the detector frame for change in $\phi$ and constant $\theta$ in the lab frame

$D2P=\sqrt{(x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2}$

$D1P=\sqrt{(x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2}$

$x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae$

$x_{D1}=r_{D1}\ cos(\phi)\qquad y_{D1}=r_{D1}cos(\phi)\qquad z_{D1}=r_{D1} cot(\theta)$

$x_{D2}=r_{D2} cos(\phi)\qquad y_{D2}=r_{D2} sin(\phi)\qquad z_{D2}=r_{D2} cot(\theta)$

$x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}$

$y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}$

$z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}$

$x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae$

$x_1^'=\frac{x_{D2}^2-2x_Px_{D2}+x_P^2+y_{D2}^2-2y_Py_{D2}+y_P^2+z_{D2}^2-2z_Pz_{D2}+z_P^2-x_P^2+2x_Px_{D1}-x_{D1}^2-y_P^2+2y_Py_{D1}-y_{D1}^2-z_P^2+2z_Pz_{D1}-z_{D1}^2}{4ae}-ae$

$x_1^'=\frac{(x_{D2}^2+y_{D2}^2)-(x_{D1}^2+y_{D1}^2)+z_{D2}^2-z_{D1}^2-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae$

$x_1^'=\frac{(r_{D2}^2)-(r_{D1}^2)+cot^2(\theta)(r_{D2}^2-r_{D1}^2)-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae$

Expressing this as functions of $\phi$ and non-differentiable constants

$x_1^'=\frac{c_1+c_2-2x_P(\phi)x_{D2}(\phi)+2x_P(\phi)x_{D1}(\phi)-2y_P(\phi)y_{D2}(\phi)+2y_P(\phi)y_{D1}(\phi)-2z_P(\phi)c_3}{4c_4}-c_4$

Differentiating with respect to $\phi$

$x_{D1}=r_{D1} cos(\phi)\Rightarrow \dot x_{D1}=-r_{D1} sin(\phi)$

$y_{D1}=r_{D1}sin(\phi)\Rightarrow \dot y_{D1}=r_{D1}cos(\phi)$

$x_{D2}=r_{D2} cos(\phi)\Rightarrow \dot x_{D2}=-r_{D2} sin(\phi)$

$y_{D2}=r_{D2}sin(\phi)\Rightarrow \dot y_{D2}=r_{D2}cos(\phi)$

$x_P=\frac{2.52934271645cos(\phi)}{cot(\theta)+cos(\phi)cot(65^{\circ})}\Rightarrow \dot x_P=\frac{-2.52934271645cot(\theta)sin(\phi)}{(cos(\phi)cot(65^{\circ}+cot(\theta))^2}$

$y_P=\frac{2.52934271645sin(\phi)}{cot(\theta)+cos(\phi)cot(65^{\circ})}\Rightarrow \dot y_P=\frac{-1.7206+2.52934271645 cos(\phi) cot(\theta)}{(cos(\phi) cot(65^{\circ}) + cot(\theta))^2}$

$z_P=\frac{2.52934271645cot(\theta)}{cot(\theta)+cos(\phi)cot(65^{\circ})}\Rightarrow \dot z_P=\frac{-1.7206 cot(\theta)sin(\phi))}{(cos(\phi) cot(65) + cot(\theta))^2}$

$\frac{dx_1^1}{d\phi}=\frac{-2}{4c_4}\frac{d}{d\phi}(x_P(\phi)x_{D2}(\phi))+\frac{2}{4c_4}\frac{d}{d\phi}(x_P(\phi)x_{D1}(\phi))-\frac{2}{4c_4}\frac{d}{d\phi}(y_P(\phi)y_{D2}(\phi))+\frac{2}{4c_4}\frac{d}{d\phi}(y_P(\phi)y_{D1}(\phi))-\frac{2c_3}{4c_4}\frac{d}{d\phi}z_P(\phi)$

$\frac{dx_1^1}{d\phi}=\frac{-2}{4c_4} \left ( (\dot x_P(\phi)x_{D2}(\phi)+x_P(\phi)\dot x_{D2}(\phi))-(\dot x_P(\phi)x_{D1}(\phi)+x_P(\phi)\dot x_{D1}(\phi))+(\dot y_P(\phi)y_{D2}(\phi)+y_P(\phi)\dot y_{D2}(\phi))-(\dot y_P(\phi)y_{D1}(\phi)+y_P(\phi)\dot y_{D1}(\phi))+c_3\dot z_P(\phi) \right )$

Function for the wire number in the detector frame for change in $\phi$ and constant $\theta$ in the lab frame

Using the expression for wire number n in terms of $\theta$ for the detector mid-plane where $\phi=0$:

$n = \frac{-957.412}{\tan(\theta)+2.14437}+430.626$

We can use the inverse of this function to find the neighboring wire's corresponding angle theta

$\theta\equiv 4.49876 +0.293001 n+0.000679074 n^2-3.57132\times 10^{-6} n^3$

$\theta(n \pm 1)\equiv 4.49876 +0.293001 (n \pm 1)+0.000679074 (n \pm 1)^2-3.57132\times 10^{-6} (n \pm 1)^3$

We also know what the x' function must follow dependent on phi in the detector plane

$x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae$

$x_1^'=\frac{(r_{D2}^2)-(r_{D1}^2)+cot^2(\theta)(r_{D2}^2-r_{D1}^2)-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae$

$x_{D1}=r_{D1}\ cos(\phi)\qquad y_{D1}=r_{D1}cos(\phi)\qquad z_{D1}=r_{D1} cot(\theta)$

$x_{D2}=r_{D2} cos(\phi)\qquad y_{D2}=r_{D2} sin(\phi)\qquad z_{D2}=r_{D2} cot(\theta)$

$x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}$

$y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}$

$z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}$

$r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(65^{\circ})cos(\theta)\qquad \qquad r_{D2}=R_{Lower\ Dandelin}cos(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)$

We can take this point to be the x axis intercept and use the fact that each wire is titled by 6 degrees to the horizontal in the plane of the detector to create an equation

$x_{wire\ n}'=tan(6^{\circ})y'+x_{n_0}$

where the initial wire and x' position at the given theta is represented by $n_0$

This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.

$\frac{x_{n=1}}{sin 4.79^{\circ}}=\frac{2.52934}{sin 110.21^{\circ}} \Rightarrow x_{n=1}=.2252$

Since each wire is separated by .01337 meters

$.2252-.01337=.2117=x_{n=0}$

Each wire becomes an equation of the form,

$x_{wire\ n}'=tan(6^{\circ})y'+.2117+.01337\ n$

This agrees with CED simulation

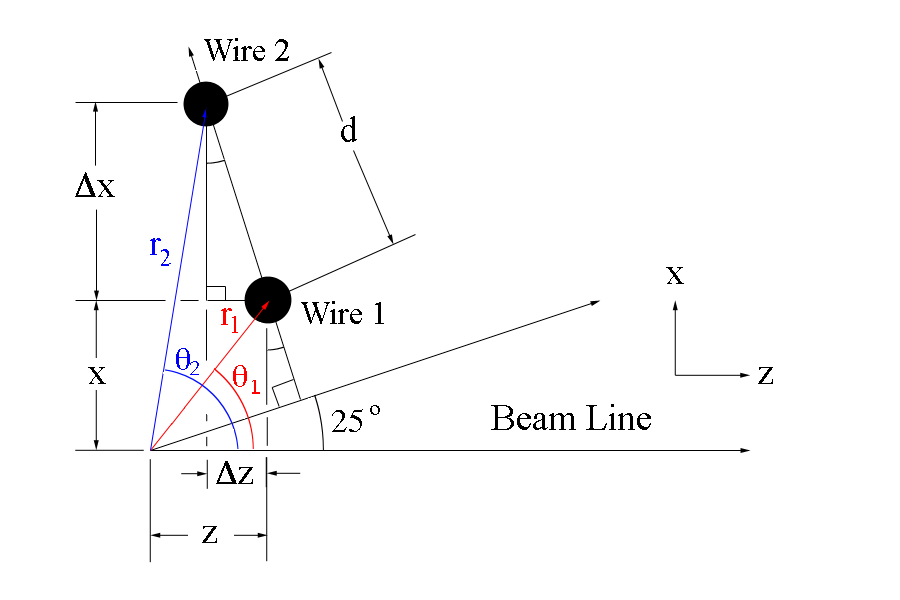
Setting up Mathematica for DC Theta-Phi Isotropic Cone

File:FirstPass.pdf

File:SecondPass.pdf