Determining Elliptical Equation
As found earlier
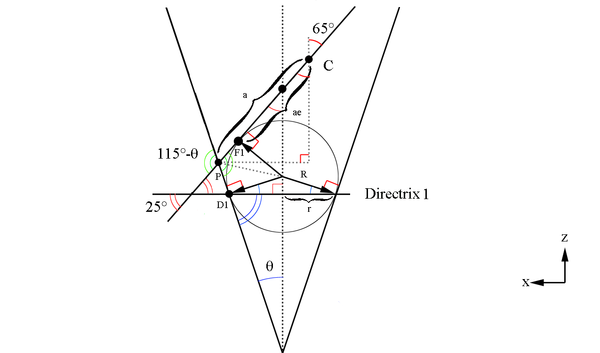
Figure 5: A cone of constant Theta with varying Phi.
[math]CP_x=a\ sin(65^{\circ})[/math]
[math]CP_z=a\ cos(65^{\circ})[/math]
Given the center point coordinates found earlier:
[math]c \equiv (-\Delta x, 0,z+\Delta z)[/math]
[math]c \equiv (-\Delta a\ sin(65^{\circ}), 0,z+\Delta a\ cos(65^{\circ}))[/math]
This gives the location of P([math]\phi=0[/math]) at
[math]P(\phi=0) \equiv (-\Delta a\ sin(65^{\circ})+a\ sin((65^{\circ}), 0,z+\Delta a\ cos(65^{\circ})-a\ cos(65^{\circ}))[/math]
[math]P(\phi=0) \equiv (-\frac{a_2-a_1}{2} sin(65^{\circ})+\frac{a_1+a_2}{2} sin((65^{\circ}), 0,2.53+\frac{a_2-a_1}{2} cos(65^{\circ})-\frac{a_1+a_2}{2} cos(65^{\circ}))[/math]
The height in z can be viewed as a linear function of x and expressed in slope intercept form for a plane:
[math]z_{Plane\ of\ sector}=m_{plane}x+b_{plane}[/math]
where
[math]m_{plane}=\frac{\Delta z}{\Delta x}=\frac{a\ cos(65^{\circ})}{-a\ sin(65^{\circ})}=-cot(65^{\circ})[/math]
[math]b_{plane}\equiv (0,0,2.53)[/math]
The D1 and D2 components can be obtained by finding the x and y components of the two directrix circles, which will be a function of their respective radii and the angle phi around the z axis.
[math]x_{Lower\ Directrix}^2+y_{Lower\ Directrix}^2=r_{Lower\ Directrix}^2\equiv r_{Lower\ Directrix}^2 cos^2(\phi)+r_{Lower\ Directrix}^2 sin^2(\phi)[/math]
Solving for the cartesian components,
[math]x_{Lower\ Directrix}=r_{Lower\ Directrix}\ cos(\phi)\qquad \qquad \qquad y_{Lower\ Directrix}=r_{Lower\ Directrix}\ sin(\phi)[/math]
Similarly,
[math]x_{Upper\ Directrix}=r_{Upper\ Directrix}\ cos(\phi)\qquad \qquad \qquad y_{Upper\ Directrix}=r_{Upper\ Directrix}\ sin(\phi)[/math]
Using the radius information found earlier for the upper and lower Dandelin spheres and directrix,
[math]R_{Lower\ Dandelin}=(ae-\Delta a) tan(65^{\circ})\qquad \qquad \qquad R_{Upper\ Dandelin}=(ae+\Delta a) tan(65^{\circ})[/math]
[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(65^{\circ})sec(\theta)\qquad \qquad\ \qquad r_{D2}=R_{Upper\ Dandelin}cos(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)[/math]
[math]r_{D1}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta)\qquad \qquad \qquad r_{D2}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{sec(\theta)}+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta)[/math]
The height to the first directrix circle is
[math]z_{D1}=r_{D1}\ cot(\theta)[/math]
The height to the second directrix circle is
[math]z_{D2}=r_{D2}\ cot(\theta)[/math]
This gives the components for a point on the directrix circles as
| [math]x_{D1}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) cos(\phi)\qquad \qquad y_{D1}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) sin(\phi)\qquad \qquad z_{D1}=r_{D1}\ cot(\theta)[/math]
|
| [math]x_{D2}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) cos(\phi)\qquad \qquad y_{D2}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) sin(\phi)\qquad \qquad z_{D2}=r_{D2}\ cot(\theta)[/math]
|
Using these two points, which will be at the same angle phi around the z axis, a line can be created
[math]\vec d=r_{D2}cos(\phi)-r_{D1}cos(\phi)\ \hat x+r_{D2}sin(\phi)-r_{D1}sin(\phi)\ \hat y+r_{D2}cot(\theta)-r_{D1}cot(\theta)\ \hat z[/math]
Since this line is composed of the difference in the cartesian components of the two points it acts as a direction vector pointing from one point to the next. We can use the fact that a line in space is simply the intersection of two planes which in this situation results in the direction vector. Finding the parametric form equation of this line
[math](x,y,z)=(r_{D1}cos(\phi),\ r_{D1}sin(\phi),\ r_{D1}cot(\theta))+t(r_{D2}cos(\phi)-r_{D1}cos(\phi),\ r_{D2}sin(\phi)-r_{D1}sin(\phi),\ r_{D2}cot(\theta)-r_{D1}cot(\theta))[/math]
Solving for the individual cartesian components
[math]x=r_{D1}cos(\phi)+t(r_{D2}cos(\phi)-r_{D1}cos(\phi))\qquad \qquad y=r_{D1}sin(\phi)+t(r_{D2}sin(\phi)-r_{D1}sin(\phi))\qquad \qquad z=r_{D1}cot(\theta)+t(r_{D2}cot(\theta)-r_{D1}cot(\theta))[/math]
[math]\Rightarrow t=\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]
Since this condition implies that the 3 equations listed above for all conditions, we can solve for the [math]\phi=0[/math] situation which must then hold for all other instances of [math]\phi[/math]
[math]\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]
[math]\frac{x-r_{D1}cos(\phi)}{(r_{D2}-r_{D1})cos(\phi)}=\frac{z-r_{D1}cot(\theta)}{(r_{D2}-r_{D1})cot(\theta)}[/math]
[math]\frac{(x-r_{D1}cos(\phi))(r_{D2}-r_{D1})cot(\theta)}{(r_{D2}-r_{D1})cos(\phi)}+r_{D1}cot(\theta)=z[/math]
Using the condition that on the plane
[math]z_{plane}=-cot(65^{\circ})x+2.53[/math]
We can substitute for z to find the point of intersection for the plane and cone at a given [math]\theta[/math] and [math]\phi[/math]
[math]\frac{ \left( x_P-r_{D1}cos(\phi) \right) cot(\theta)}{cos(\phi)}+r_{D1}cot(\theta)=-cot(65^{\circ})x_P+2.53[/math]
[math] \left ( \frac{x_P}{cos(\phi)}+r_{D1}-r_{D1} \right )cot(\theta )=-cot(65^{\circ})x_P+2.53[/math]
[math] \left ( \frac{x_P}{cos(\phi)} \right )cot(\theta )+cot(65^{\circ})x_P=2.53[/math]
[math] \frac{x_P\ cot(\theta )}{cos(\phi)}+cot(65^{\circ})x_P=2.53[/math]
[math] x_P \left (\frac{ cot(\theta)+cos(\phi)cot(65^{\circ})}{cos(\phi)}\right )=2.53[/math]
[math]x_P(cot(\theta)+cos(\phi)cot(65^{\circ})=2.53cos(\phi)[/math]
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]\Rightarrow t=\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]
[math]\frac{x_P-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}[/math]
[math](r_{D2}sin(\phi)-r_{D1}sin(\phi))\frac{(x_P-r_{D1}cos(\phi))}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=y_P-r_{D1}sin(\phi)[/math]
[math](r_{D2}-r_{D1})sin(\phi)\frac{(x_P-r_{D1}cos(\phi))}{(r_{D2}-r_{D1})cos(\phi)}=y_P-r_{D1}sin(\phi)[/math]
[math]sin(\phi)\frac{(x_P-r_{D1}cos(\phi))}{cos(\phi)}=y_P-r_{D1}sin(\phi)[/math]
[math]y_P=sin(\phi)\frac{(x_P-r_{D1}cos(\phi))}{cos(\phi)}+r_{D1}sin(\phi)[/math]
[math]y_P=tan(\phi)x_P-r_{D1}sin(\phi)+r_{D1}sin(\phi)[/math]
[math]y_P=tan(\phi)x_P-r_{D1}sin(\phi)+r_{D1}sin(\phi)[/math]
[math]y_P=tan(\phi)\left (\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}\right )[/math]
| [math]y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]z_P=\frac{(x_P-r_{D1}cos(\phi))(r_{D2}-r_{D1})cot(\theta)}{(r_{D2}-r_{D1})cos(\phi)}+r_{D1}cot(\theta)[/math]
[math]z_P=\frac{(x_P)cot(\theta)}{cos(\phi)}[/math]
[math]z_P=\frac{(\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})})cot(\theta)}{cos(\phi)}[/math]
| [math]z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
Test for [math]\theta=20[/math] and [math]\phi=0[/math]
Solving for the components of the ellipse
[math]a_1=\frac{2.53sin(\theta)}{sin(115-\theta)}=\frac{2.53sin(20^{\circ})}{sin(115^{\circ}-20^{\circ})}=\frac{2.53\cdot.342}{.9962}=.8686[/math]
[math]a_2=\frac{2.53sin(\theta)}{sin(65-\theta)}=\frac{2.53sin(20^{\circ})}{sin(65^{\circ}-20^{\circ})}=\frac{2.53\cdot.342}{.0872}=1.2237[/math]
[math]c_{ellipse} \equiv (-\Delta a\ sin(65^{\circ}), 0,z+\Delta a\ cos(65^{\circ}))[/math]
[math]c_{ellipse} \equiv (-\frac{a_2-a_1}{2} sin(65^{\circ}), 0,2.53+\frac{a_2-a_1}{2} cos(65^{\circ}))[/math]
[math]c_{ellipse} \equiv (-\frac{1.2237-.8686}{2} sin(65^{\circ}), 0,2.53+\frac{1.2237-.8686}{2} cos(65^{\circ}))[/math]
[math]c_{ellipse} \equiv (-\frac{.3550}{2} sin(65^{\circ}), 0,2.53+\frac{.3550}{2} cos(65^{\circ}))[/math]
[math]c_{ellipse} \equiv (-.1775 sin(65^{\circ}), 0,2.53+.1775 cos(65^{\circ}))[/math]
[math]c_{ellipse} \equiv (-.1609, 0,.0750)[/math]
[math]P(\phi=0) \equiv (-\frac{a_2-a_1}{2} sin(65^{\circ})+\frac{a_1+a_2}{2} sin((65^{\circ}), 0,2.53+\frac{a_2-a_1}{2} cos(65^{\circ})-\frac{a_1+a_2}{2} cos(65^{\circ}))[/math]
[math]P(\phi=0) \equiv (-\frac{1.2234-.8684}{2} sin(65^{\circ})+\frac{.8684+1.2234}{2} sin((65^{\circ}), 0,2.53+\frac{1.2234-.8684}{2} cos(65^{\circ})-\frac{.8684+1.2234}{2} cos(65^{\circ}))[/math]
[math]P(\phi=0) \equiv (-\frac{.3550}{2} sin(65^{\circ})+\frac{2.0918}{2} sin((65^{\circ}), 0,2.53+\frac{.3550}{2} cos(65^{\circ})-\frac{2.0918}{2} cos(65^{\circ}))[/math]
[math]P(\phi=0) \equiv (-.1775 sin(65^{\circ})+1.0459 sin((65^{\circ}), 0,2.53+.1775 cos(65^{\circ})-1.0459 cos(65^{\circ}))[/math]
[math]P(\phi=0) \equiv (.7870, 0,2.1623)[/math]
[math]x=\frac{2.53cos(\phi)}{cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
[math]x=\frac{2.53cos(0)}{cot(20^{\circ})+cos(0)cot(65^{\circ})}[/math]
[math]x=\frac{2.53}{2.7475+.4663}[/math]
[math]x=\frac{2.53}{3.2138}=.7870\text{cm}[/math]
The y component is zero for [math]\phi=0[/math]
The z component can be found from the ellipse equation
[math]z=-cot(65^{\circ})x+2.53=-cot(65^{\circ})(.7870)+2.53=2.1623\ \text{cm}[/math]
[math]e\equiv \frac{sin(25^{\circ})}{cos(20^{\circ})}=0.96447[/math]
[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(65^{\circ})cos(\theta)\qquad \qquad r_{D2}=R_{Lower\ Dandelin}cos(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)[/math]
[math]r_{D1}=(\frac{a_1+a_2}{2}e-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta)\qquad \qquad r_{D2}=(\frac{a_1+a_2}{2}e+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta)[/math]
[math]r_{D1}=(\frac{.8686+1.2237}{2}e-\frac{1.2237-.8686}{2}) tan(65^{\circ})cos(\theta)\qquad \qquad r_{D2}=(\frac{.8686+1.2237}{2}e+\frac{1.2237-.8686}{2}) tan(65^{\circ})cos(\theta)[/math]
[math]r_{D1}=(\frac{2.0923}{2}\frac{sin(25^{\circ})}{cos(20^{\circ})}-\frac{.3551}{2}) tan(65^{\circ})cos(20^{\circ})\qquad \qquad r_{D2}=(\frac{2.0923}{2}\frac{sin(25^{\circ})}{cos(20^{\circ})}+\frac{.3551}{2}) tan(65^{\circ})cos(20^{\circ}))[/math]
[math]r_{D1}=(\frac{2.0923}{2}\frac{sin(25^{\circ})}{cos(20^{\circ})}-\frac{.3551}{2}) tan(65^{\circ})cos(20^{\circ})\qquad \qquad r_{D2}=(\frac{2.0923}{2}\frac{sin(25^{\circ})}{cos(20^{\circ})}+\frac{.3551}{2}) tan(65^{\circ})cos(20^{\circ}))[/math]
[math]r_{D1}=(1.0459(.4497)-.1775)\cdot 2.1445\cdot .9397=.5901\ \text{m} \qquad \qquad r_{D2}=(1.0459(.4497)+.1775)\cdot 2.1445\cdot .9397=1.3055 \text{m}[/math]
The height to the first directrix circle is
[math]z_{D1}=r_{D1} cot(\theta)=.5901cot(20)=1.6212[/math]
and the x and y components are
[math]x_{D1}=r_{D1}\ cos(\phi)=.5901 cos(0)=.5901\text {m}\ \ \ \ y_{D1}=r_{D1}cos(\phi)=.5901 sin(0)=0[/math]
The height to the second directrix circle is
[math]z_{D2}=r_{D2} cot(\theta)=1.3055cot(20)=3.5868\ \text{m}[/math]
and the x and y components are
[math]x_{D2}=r_{D2} cos(\phi)=1.3055cos(0)=1.3055\text {m}\ \ \ \ y_{D2}=r_{D2} sin(\phi)=1.3055sin(0)=0[/math]
The distance between the two point
[math]\sqrt{(1.3055-.5901)^2+(0-0)^2+(3.5868-1.6212)^2}=\sqrt{.715^2+1.9656^2}=2.09\text {m}[/math]
This should be equal to 2a
[math]2a=2(\frac{a_1+a_2}{2})=2(\frac{.8684+1.2234}{2})=2.09\text {m}[/math]
This gives the components for a point on the directrix circles as
| [math]x_{D1}=r_{D1}\ cos(\phi)=.5901cos(0)=.5901\text {m}\qquad y_{D1}=r_{D1}cos(\phi)=.5901 sin(0)=0\qquad z_{D1}=r_{D1} cot(\theta)=.5901cot(20)=1.6212\ \text{m}[/math]
|
| [math]x_{D2}=r_{D2} cos(\phi)=1.3055cos(0)=1.3055\text {m}\qquad y_{D2}=r_{D2} sin(\phi)=1.3055sin(0)=0\qquad z_{D2}=r_{D2} cot(\theta)=1.3055cot(20)=3.5868\ \text{m}[/math]
|
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53cos(0)}{(cot(20^{\circ})+cos(0)cot(65^{\circ})}=0.7872\qquad y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53sin(0)}{(cot(20^{\circ})+cos(0)cot(65^{\circ})}=0\qquad z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53cot(20^{\circ})}{(cot(20^{\circ})+cos(0)cot(65^{\circ})}=2.1623[/math]
|
[math]D2P=\sqrt{(x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2}=\sqrt{(1.3055-0.7872)^2+(0-0)^2+(3.5868-2.1623)^2}=\sqrt{(.5183)^2+(1.445)^2}=\sqrt{.2686+2.0292}=1.5158611\ \text{m}[/math]
[math]D1P=\sqrt{(x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2}=\sqrt{(0.7872-.5901)^2+(0-0)^2+(2.1623-1.6212)^2}=\sqrt{(.1971)^2+(.5411)^2}=\sqrt{.0388+.2927}=.575879865944\ \text{m}[/math]
In the plane
We can use the geometry of the sector to impose limits on the allowed x and y for this plane. The angle which the two sides of the triangle that make up the sector is given as [math]59^{\circ}[/math]. Each focii will have a ray that creates a circle around the point that is equal to the length found from the D1P and D2P lines. These circles will overlap at a common y component, which can be used to determine if the point is within the detector limits.
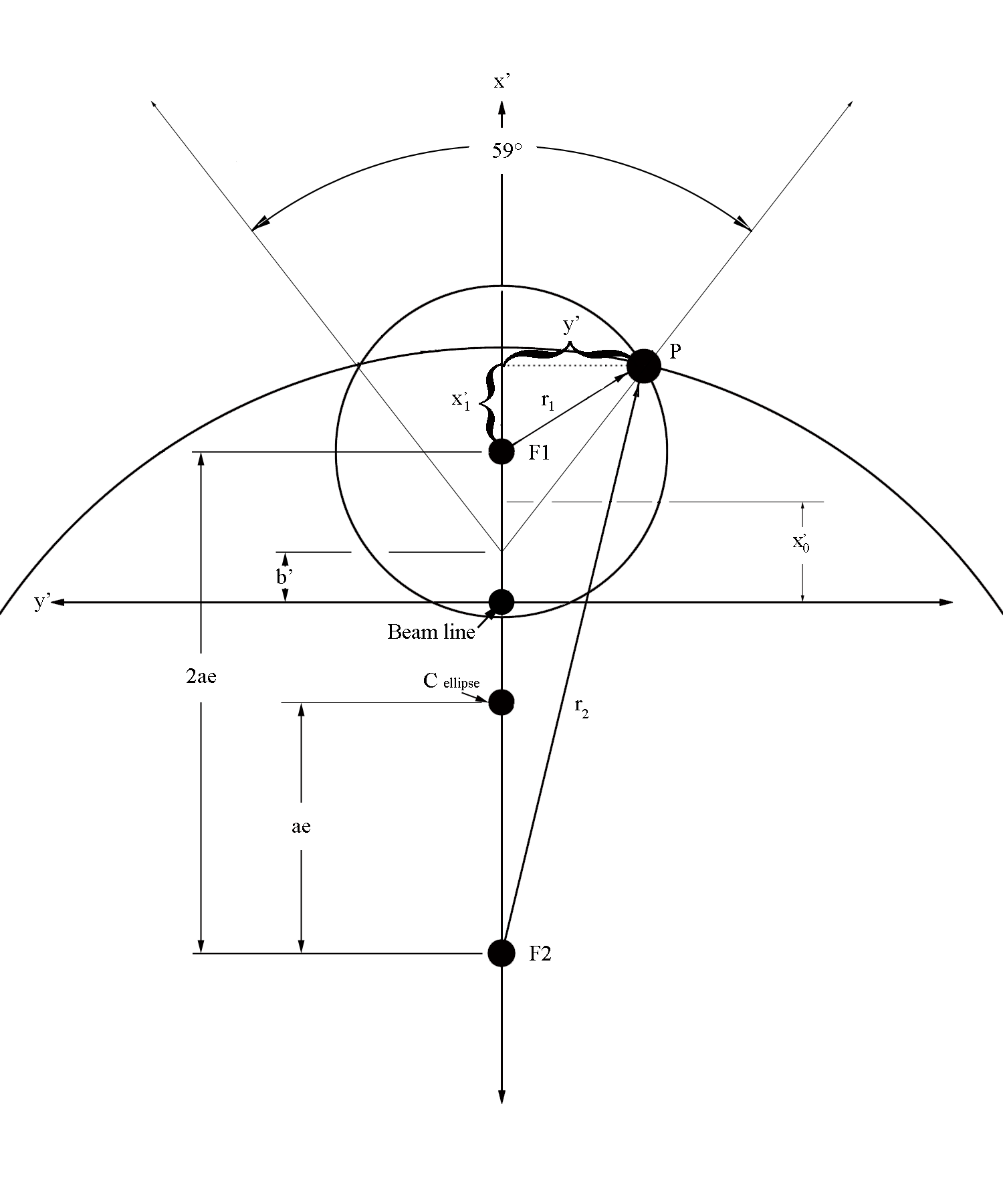
Using the physical constraints of the distance the interior walls of the side walls intersect each other from the beam line, as well as the angle the lowest guard wire at the plane midpoint.
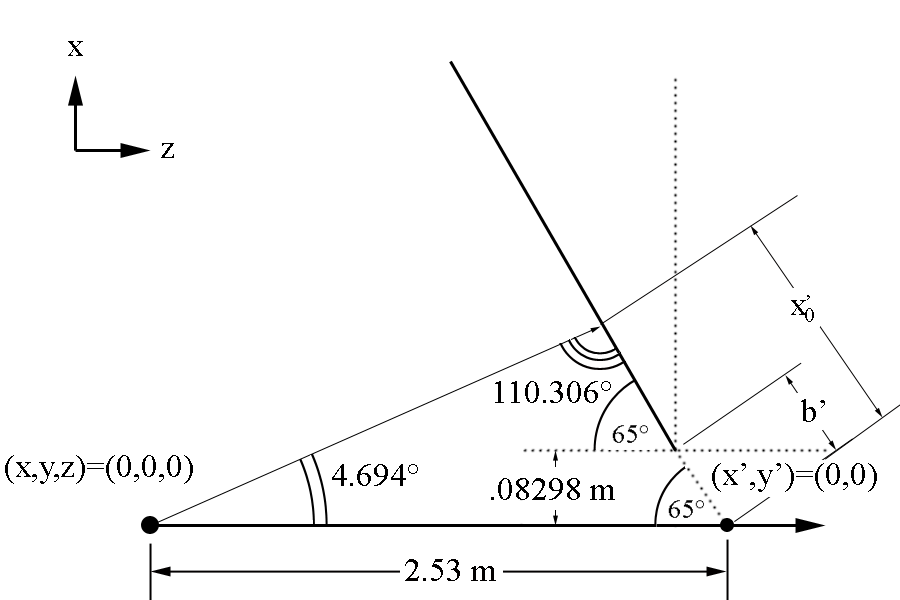
where b' is the location on the y' axis where the two interior side walls of the sector intersect.
[math]b'=\frac{0.08298\ m}{sin(65^{\circ})}=.09156\ m[/math]
The quantity [math]x_0^'[/math] is the corresponding x' distance from the beam line and detector plane intersection.
[math]\frac{x_0^'}{sin(4.694^{\circ})}=\frac{2.53\ m}{sin(110.306^{\circ})}[/math]
[math]x_0^'=\frac{sin(4.694^{\circ})2.53\ m}{sin(110.306^{\circ})}=.0872(2.53)=.22070/ m[/math]
Since the interior sides of the sector make an angle of [math]59^{\circ}[/math] in the plane of the wires, this can be represented by equations
[math]x'=\pm cot(29.5^{\circ})y^'+.09156\ m[/math]
Using the properties of an ellipse, we can work in the coordinates of the ellipse, in the plane of the ellipse, where the vertex is located at the crossing of the ellipse and the cone. Since the Dandelin construction was used, we know that
[math]F1P=D1P\qquad \text{and}\ F2P=D2P[/math]
If we shift the origin from the center of the ellipse to the intersection of the plane and cone for a given theta
[math]c_{ellipse}\equiv(-\Delta a,0)[/math]
[math]F1\equiv (-\Delta a+ae,0)\qquad F2\equiv (-\Delta a-ae,0)[/math]
Writing the equations for circles centered at an ellipse focii points, we find
[math]x_1^{'2}+y_1^{'2}=r_1^{'2}\qquad \qquad x_2+^{'2}+y_2^{'}2=r_2^{'2}[/math]
[math]r_1^{'2}-x_1^{'2}=y_1^{'2}\qquad \qquad y_2^{'2}=r_2^{'2}-x_2^{'2}[/math]
Since the focii are seperated by 2ae as found earlier
[math]x_2^'=x_1^'+2ae[/math]
[math]r_1^{'2}-x_1^{'2}=r_2^{'2}-(x_1^'+2ae)^2[/math]
[math]r_1^{'2}-r_2^{'2}=-4x_1^'ae-4a^2e^2[/math]
[math]r_2^{'2}-r_1^{'2}=8ae(x_1^'+ae+\Delta a)[/math]
[math]\frac{r_2^{'2}-r_1^{'2}}{4ae}-ae=x_1^'[/math]
Test for [math]\theta=20[/math] and [math]\phi=0[/math]
Substituting in the values found earlier for the case of [math]\theta=20^{\circ}[/math] and [math]\phi=0[/math]
[math]a=\frac{a_1+a_2}{2}=1.0459[/math]
[math]e\equiv \frac{sin(25^{\circ})}{cos(\theta)}= \frac{sin(25^{\circ})}{cos(20^{\circ})}=.4497[/math]
[math]x_1^'=\frac{r_2^{'2}-r_1^{'2}}{4ae}-ae=\frac{r_2^{'2}-r_1^{'2}}{4(1.0459)(.4497)}-(1.0459)(.4497)[/math]
Since
[math]\lVert \overrightarrow{D1P} \rVert \equiv \lVert \overrightarrow{F1P} \rVert \qquad \qquad \lVert \overrightarrow{D2P} \rVert \equiv \lVert \overrightarrow{F2P} \rVert[/math]
[math]D1P \approx .576\ \text{m}\qquad D2P \approx 1.516\ \text{m}[/math]
The [math]x_1^' [/math] distance from focal point 1 is:
[math]x_1^'=\frac{1.516^2-.576^2}{4(1.0459)(.4497)}-(1.0459)(.4497)=\frac{1.97}{1.88}-.4703=.576\ \text{m}=r_1[/math]
This is the radius from focal point 1, which is to be expected since the y component is equal to zero for [math]\phi=0[/math]
The focii are located at
[math]F1\equiv (-\Delta a+ae,0)=(-.1775+1.0459(.4497),0)=(.292,0)\ \text{m}\qquad F2\equiv (-\Delta a-ae,0)=(-.1775-1.0450(.4497),0)=(-6.478,0)\ \text{m}[/math]
This implies that with respect to the origin, x', we find
[math]x'=x_1'+\Delta a+ae=.576+.292=.868\ \text{m}[/math]
This is verified with CED
Since the x' dimension is the hypotenuse in a right triangle of 65 degrees
[math]x'=\frac{x_{lab}}{sin 65^{ \circ}}=.868=x'[/math]
Test for [math]\theta=20[/math] and [math]\phi=1[/math]
All previous quantities where calculated for [math]\theta=20^{\circ}[/math] and do not depend on the angle [math]\phi[/math]. The quantities that do change
| [math]x_{D1}=r_{D1}\ cos(\phi)=.5901cos(1^{\circ}))=.5900\text {m}\qquad y_{D1}=r_{D1}cos(\phi)=.5901 sin(1^{\circ}))=.0103\qquad z_{D1}=r_{D1} cot(\theta)=.5901cot(20)=1.6212\ \text{m}[/math]
|
| [math]x_{D2}=r_{D2} cos(\phi)=1.3055cos(1^{\circ}))=1.3053\text {m}\qquad y_{D2}=r_{D2} sin(\phi)=1.3055sin(1^{\circ}))=.0228\qquad z_{D2}=r_{D2} cot(\theta)=1.3055cot(20)=3.5868\ \text{m}[/math]
|
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53cos(1^{\circ}))}{(cot(20^{\circ})+cos(1^{\circ}))cot(65^{\circ})}=0.7869[/math]
|
| [math]y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53sin(1^{\circ}))}{(cot(20^{\circ})+cos(1^{\circ}))cot(65^{\circ})}=.0137[/math]
|
| [math]z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}=\frac{2.53cot(20^{\circ})}{(cot(20^{\circ})+cos(1^{\circ}))cot(65^{\circ})}=2.1624[/math]
|
[math]D2P=\sqrt{(x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2}=\sqrt{(1.3053-0.7869)^2+(.0228-.0137)^2+(3.5868-2.1624)^2}=\sqrt{(.5184)^2+(.0091)^2+(1.4244)^2}=1.51582872713\ \text{m}[/math]
[math]D1P=\sqrt{(x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2}=\sqrt{(0.7871-.5900)^2+(.0137-.0103)^2+(2.1624-1.6212)^2}=\sqrt{(.1971)^2+(.0034)^2+(.5412)^2}=.575983862621\ \text{m}[/math]
[math]x_1^'=\frac{r_2^{'2}-r_1^{'2}}{4ae}-ae=\frac{1.5158^{'2}-.5758^{'2}}{4(1.0459)(.4497)}-(1.0459)(.4497)=.575\ \text{m}[/math]
Using the pythagorean theorem
[math]y'=\sqrt{.576^2-.575^2}=.03\ \text{m}[/math]
The two possible answers denote shifting to the left on right on the y axis. We take the direction of positive and negative to be the same as the sign convention for the angle phi starting on the x axis and shifting positive clockwise. A shift of 1 degree in phi at theta equal to 20 degrees only results in a small change in the x and y. This changes depending on the angles.
Function for the change in x' in the detector frame for change in [math]\phi[/math] and constant [math]\theta[/math] in the lab frame
[math]D2P=\sqrt{(x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2}[/math]
[math]D1P=\sqrt{(x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2}[/math]
[math]x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae[/math]
| [math]x_{D1}=r_{D1}\ cos(\phi)\qquad y_{D1}=r_{D1}cos(\phi)\qquad z_{D1}=r_{D1} cot(\theta)[/math]
|
| [math]x_{D2}=r_{D2} cos(\phi)\qquad y_{D2}=r_{D2} sin(\phi)\qquad z_{D2}=r_{D2} cot(\theta)[/math]
|
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
| [math]y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
| [math]z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae[/math]
[math]x_1^'=\frac{x_{D2}^2-2x_Px_{D2}+x_P^2+y_{D2}^2-2y_Py_{D2}+y_P^2+z_{D2}^2-2z_Pz_{D2}+z_P^2-x_P^2+2x_Px_{D1}-x_{D1}^2-y_P^2+2y_Py_{D1}-y_{D1}^2-z_P^2+2z_Pz_{D1}-z_{D1}^2}{4ae}-ae[/math]
[math]x_1^'=\frac{(x_{D2}^2+y_{D2}^2)-(x_{D1}^2+y_{D1}^2)+z_{D2}^2-z_{D1}^2-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae[/math]
[math]x_1^'=\frac{(r_{D2}^2)-(r_{D1}^2)+cot^2(\theta)(r_{D2}^2-r_{D1}^2)-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae[/math]
Expressing this as functions of [math]\phi[/math] and non-differentiable constants
[math]x_1^'=\frac{c_1+c_2-2x_P(\phi)x_{D2}(\phi)+2x_P(\phi)x_{D1}(\phi)-2y_P(\phi)y_{D2}(\phi)+2y_P(\phi)y_{D1}(\phi)-2z_P(\phi)c_3}{4c_4}-c_4[/math]
Differentiating with respect to [math]\phi[/math]
| [math]x_{D1}=r_{D1} cos(\phi)\Rightarrow \dot x_{D1}=-r_{D1} sin(\phi)[/math]
|
| [math]y_{D1}=r_{D1}sin(\phi)\Rightarrow \dot y_{D1}=r_{D1}cos(\phi)[/math]
|
| [math]x_{D2}=r_{D2} cos(\phi)\Rightarrow \dot x_{D2}=-r_{D2} sin(\phi)[/math]
|
| [math]y_{D2}=r_{D2}sin(\phi)\Rightarrow \dot y_{D2}=r_{D2}cos(\phi)[/math]
|
| [math]x_P=\frac{2.52934271645cos(\phi)}{cot(\theta)+cos(\phi)cot(65^{\circ})}\Rightarrow \dot x_P=\frac{-2.52934271645cot(\theta)sin(\phi)}{(cos(\phi)cot(65^{\circ}+cot(\theta))^2}[/math]
|
| [math]y_P=\frac{2.52934271645sin(\phi)}{cot(\theta)+cos(\phi)cot(65^{\circ})}\Rightarrow \dot y_P=\frac{-1.7206+2.52934271645 cos(\phi) cot(\theta)}{(cos(\phi) cot(65^{\circ}) + cot(\theta))^2}[/math]
|
| [math]z_P=\frac{2.52934271645cot(\theta)}{cot(\theta)+cos(\phi)cot(65^{\circ})}\Rightarrow \dot z_P=\frac{-1.7206 cot(\theta)sin(\phi))}{(cos(\phi) cot(65) + cot(\theta))^2}[/math]
|
[math]\frac{dx_1^1}{d\phi}=\frac{-2}{4c_4}\frac{d}{d\phi}(x_P(\phi)x_{D2}(\phi))+\frac{2}{4c_4}\frac{d}{d\phi}(x_P(\phi)x_{D1}(\phi))-\frac{2}{4c_4}\frac{d}{d\phi}(y_P(\phi)y_{D2}(\phi))+\frac{2}{4c_4}\frac{d}{d\phi}(y_P(\phi)y_{D1}(\phi))-\frac{2c_3}{4c_4}\frac{d}{d\phi}z_P(\phi)[/math]
[math]\frac{dx_1^1}{d\phi}=\frac{-2}{4c_4} \left ( (\dot x_P(\phi)x_{D2}(\phi)+x_P(\phi)\dot x_{D2}(\phi))-(\dot x_P(\phi)x_{D1}(\phi)+x_P(\phi)\dot x_{D1}(\phi))+(\dot y_P(\phi)y_{D2}(\phi)+y_P(\phi)\dot y_{D2}(\phi))-(\dot y_P(\phi)y_{D1}(\phi)+y_P(\phi)\dot y_{D1}(\phi))+c_3\dot z_P(\phi) \right )[/math]
Function for the wire number in the detector frame for change in [math]\phi[/math] and constant [math]\theta[/math] in the lab frame
Using the expression for wire number n in terms of [math]\theta[/math] for the detector mid-plane where [math]\phi=0[/math]:
[math]n = \frac{-957.412}{\tan(\theta)+2.14437}+430.626[/math]
We can use the inverse of this function to find the neighboring wire's corresponding angle theta
[math]\theta\equiv 4.49876 +0.293001 n+0.000679074 n^2-3.57132\times 10^{-6} n^3[/math]
[math]\theta(n \pm 1)\equiv 4.49876 +0.293001 (n \pm 1)+0.000679074 (n \pm 1)^2-3.57132\times 10^{-6} (n \pm 1)^3[/math]
We also know what the x' function must follow dependent on phi in the detector plane
[math]x_1^'=\frac{((x_{D2}-x_P)^2+(y_{D2}-y_P)^2+(z_{D2}-z_P)^2)-((x_P-x_{D1})^2+(y_P-y_{D1})^2+(z_P-z_{D1})^2)}{4ae}-ae[/math]
[math]x_1^'=\frac{(r_{D2}^2)-(r_{D1}^2)+cot^2(\theta)(r_{D2}^2-r_{D1}^2)-2x_P(x_{D2}-x_{D1})-2y_P(y_{D2}-y_{D1})-2z_P(z_{D2}-z_{D1})}{4ae}-ae[/math]
| [math]x_{D1}=r_{D1}\ cos(\phi)\qquad y_{D1}=r_{D1}cos(\phi)\qquad z_{D1}=r_{D1} cot(\theta)[/math]
|
| [math]x_{D2}=r_{D2} cos(\phi)\qquad y_{D2}=r_{D2} sin(\phi)\qquad z_{D2}=r_{D2} cot(\theta)[/math]
|
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
| [math]y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
| [math]z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(65^{\circ})cos(\theta)\qquad \qquad r_{D2}=R_{Lower\ Dandelin}cos(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)[/math]
We can take this point to be the x axis intercept and use the fact that each wire is titled by 6 degrees to the horizontal in the plane of the detector to create an equation
[math]x_{wire\ n}'=tan(6^{\circ})y'+x_{n_0}[/math]
where the initial wire and x' position at the given theta is represented by [math]n_0[/math]
This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.
[math]\frac{x_{n=1}}{sin 4.79^{\circ}}=\frac{2.52934}{sin 110.21^{\circ}} \Rightarrow x_{n=1}=.2252[/math]
Since each wire is separated by .01337 meters
[math].2252-.01337=.2117=x_{n=0}[/math]
Each wire becomes an equation of the form,
[math]x_{wire\ n}'=tan(6^{\circ})y'+.2117+.01337\ n[/math]
This agrees with CED simulation
Setting up Mathematica for DC Theta-Phi Isotropic Cone
File:FirstPass.pdf
File:SecondPass.pdf




