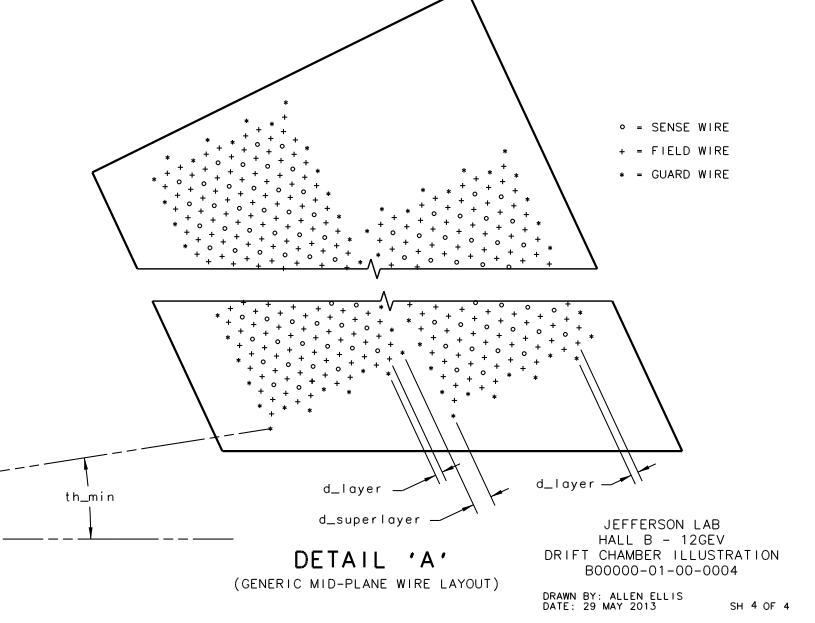
Determining wire-theta correspondence

To associate the hits with the Moller scattering angle theta, the occupancy plots of the drift chamber hits by means of wire numbers and layer must be translated using the physical constraints of the detector. Using the data released for the DC:

DC: Drift Chambers(specs)

DC Geometry(geom)

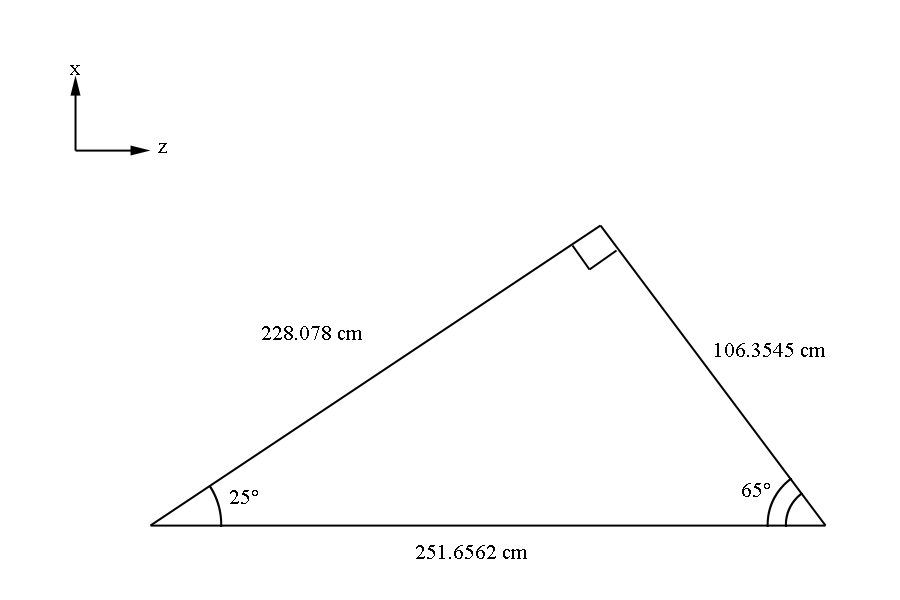
At 25 degrees to the beam line, we can create a line that is perpendicular to the wires, which are at 65 degrees. This line will be a perpendicular line with respect to all parallel layers. We can use the fact that the dist2target, which is the perpendicular length from the origin (0,0,0) to the plane of the first guard wire.

[math]\frac{228.078\ cm}{cos\ 25^{\circ}}=251.6562\ cm[/math]

The first guard wire can be found at 4.694 degrees above the beam line. This position can be taken as the starting position for the wire normal plane.

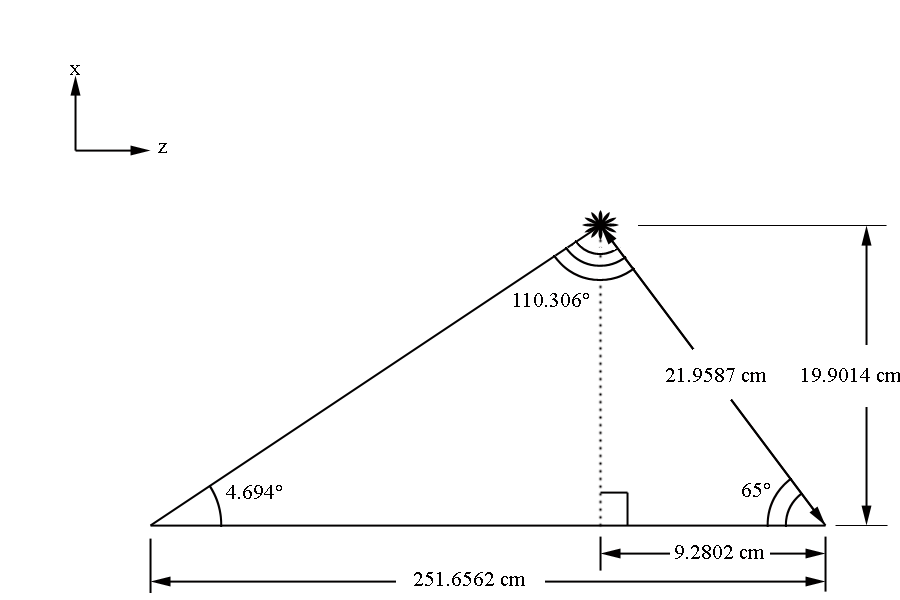
Using the law of sines

[math]\frac{251.6562}{sin\ 110.306^{\circ}}=\frac{d}{sin\ 4.694^{\circ}}\Rightarrow d=21.9587\ cm[/math]

Making a right triangle,

[math]21.9587\ cm\ sin\ 65^{\circ}=19.914\ cm\ \hat{x}[/math]

[math]21.9587\ cm\ cos\ 65^{\circ}=9.2802\ cm\ \hat{z}[/math]

Examining the geometry file, we can see that each plane, not just the plane of the sense wires, is separated by a distance of

[math]D=.3861\ cm[/math]

We can use the geometry of the wire placements to find the separation distance between two adjacent sense wires on the same plane

[math]d=4(.3861\ cm)\cos(30^{\circ})=1.337\ cm[/math]

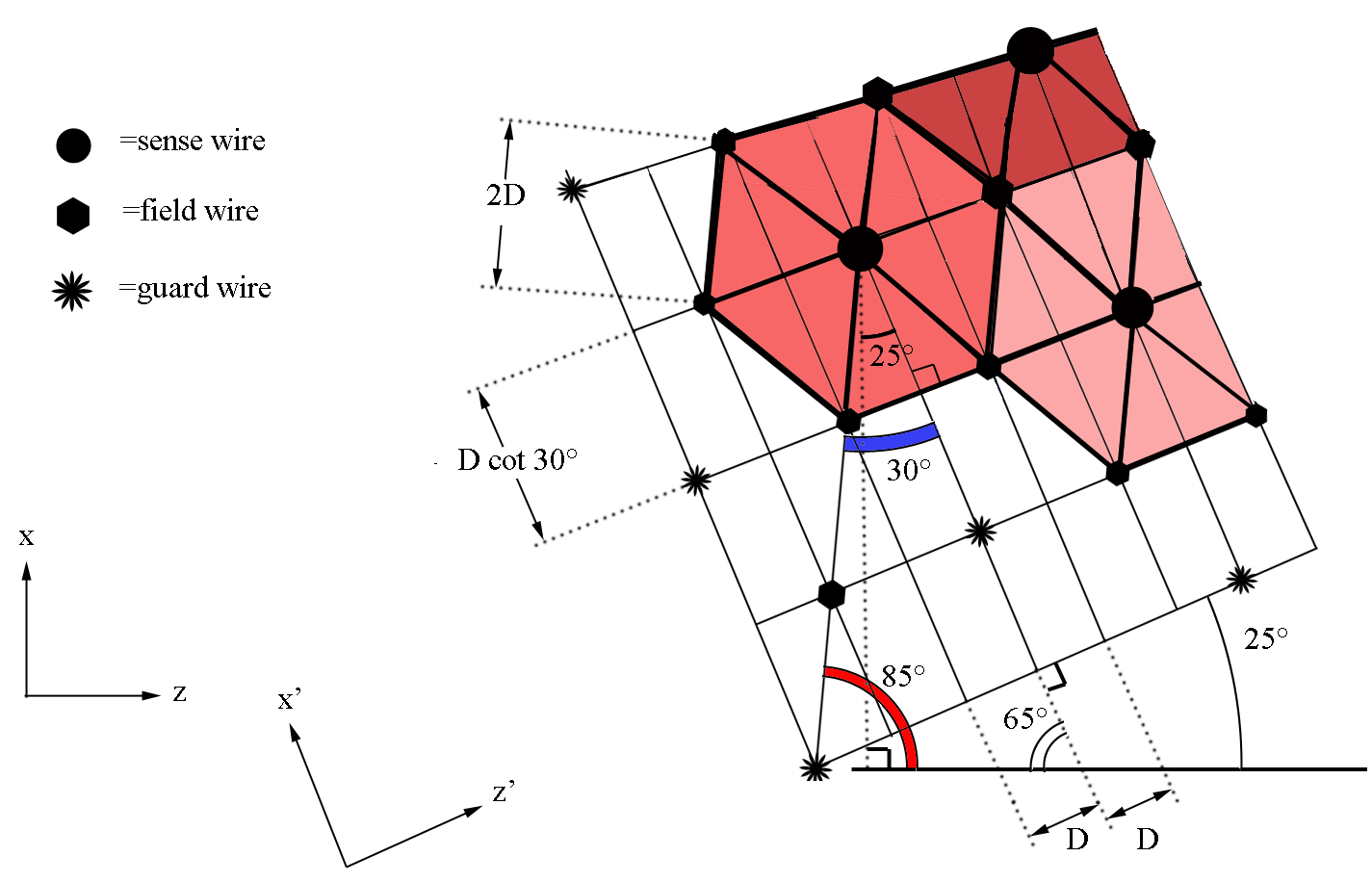
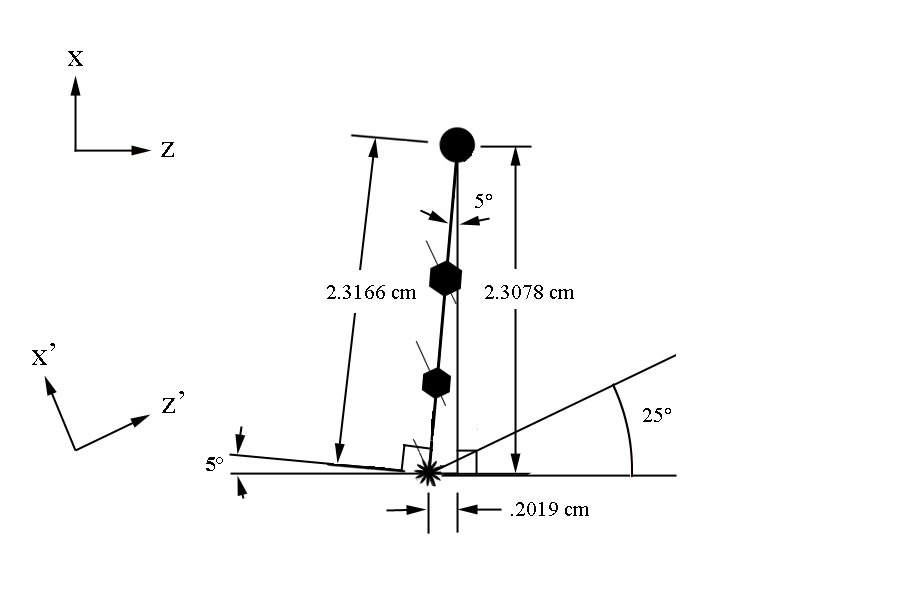
The starting position for sense wires with respect to the first guard wire at midplane, can be found to be at:

[math]2.3166\ cm\ \cos\ 5^{\circ}=2.3078\ cm\ \hat{x}[/math]

[math]2.3166\ cm\ \sin\ 5^{\circ}=.2019\ cm\ \hat{z}[/math]

Since the separation between adjacent sense wires is uniform and at a set angle of 25 degrees with respect to the beam line, we can use this fact to determine the angle theta each wire makes when measured from the vertex.

[math]\Delta\ x=1.337\cos(25^{\circ})cm=1.212cm[/math]

[math]\Delta\ z=-1.337\sin(25^{\circ})cm=-0.5652cm[/math]

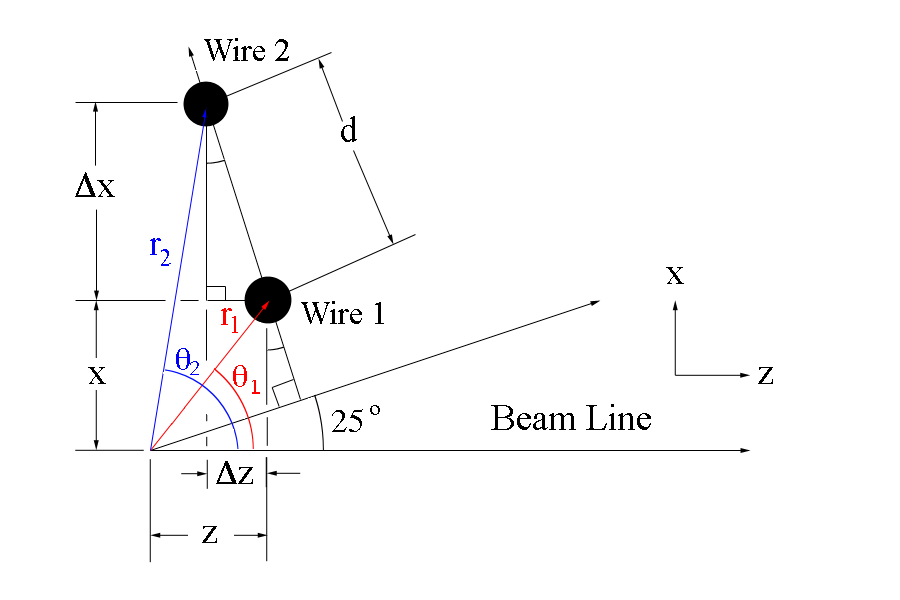
The new x and z coordinates for wire 2 can be found using the change in the components

[math]x=x_1+\Delta x[/math] [math]z=z_1+\Delta z[/math]

This can be extended to any point along the same wire plane, starting from the coordinates for wire 1 minus the difference in position to the next wire crossing on the plane.

[math]x_0=x_1-\Delta x[/math] [math]z_0=z_1-\Delta z[/math] [math]x=x_0+\Delta x\times\ n[/math] [math]z=z_0+\Delta z\times\ n[/math]

The angle theta that the wire makes with the vertex is given by

[math]\tan{\theta}=\frac{x_0+\Delta x}{z_0+\Delta z}\Rightarrow \theta=\arctan{\frac{x_0+\Delta x}{z_0+\Delta z}}[/math]

For the values found earlier for the starting position:

[math]\frac{19.9014\ cm\ +2.3078\ cm}{243.3760\ cm+.2019\ cm}=\frac{22.2092\ cm}{243.5779\ cm}=.09118=\tan\ \theta[/math]

[math]\theta=\arctan\ .09118=5.2098^{\circ}[/math]

[math]x_0=22.2092-1.212=20.9972\ cm\ \hat{x}[/math] [math]z_0=243.5779+0.5652=244.1431\ cm\ \hat{z}[/math] [math]x=x_0+\Delta x\times\ n[/math] [math]z=z_0+\Delta z\times\ n[/math]