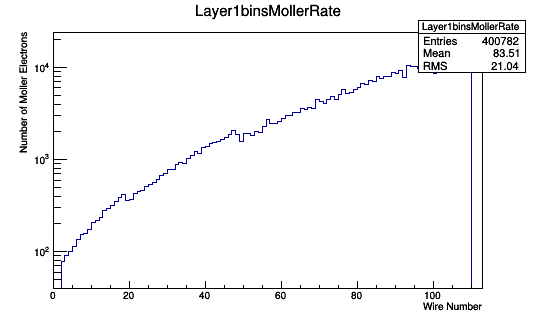
Wire angle correspondance

Straight Track Moller Rates

Goal: Confirm that the moller Rate (Hz) seen in on a wire agrees with the Rate calculated from the cross section. The torus is turned off so the wire is more easily correlated with the moller scattering angle. No need for track reconstruction.

Reproduce the plot below using Torus off

https://wiki.iac.isu.edu/index.php/File:TheoryDCHits.png

Then calculate Rate and compare to the reference.

Determining wire-theta correspondence

To associate the hits with the Moller scattering angle theta, the occupancy plots of the drift chamber hits by means of wire numbers and layer must be translated using the physical constraints of the detector. Using the data released for the DC:

DC: Drift Chambers(specs)

DC Geometry(geom)

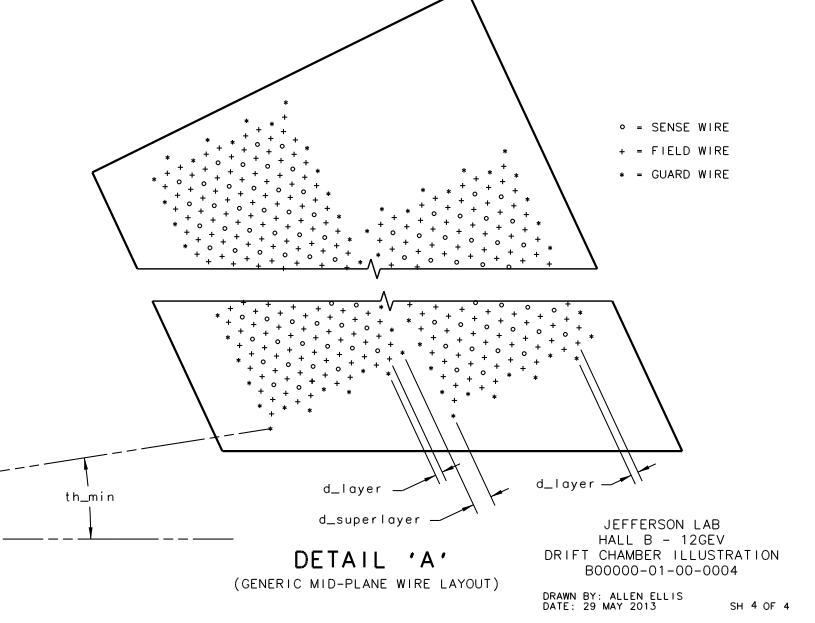
Examining the geometry file, we can see that each plane, not just the plane of the sense wires, is separated by a distance of D=.3861 cm. We can use the geometry of the wire placements to find

$\alpha=\frac{D}{\cos(60^{\circ})}=2D$

Finding the separation distance between two adjacent sense wires

$d=4(.3861\ cm)\cos(30^{\circ})=1.337\ cm$

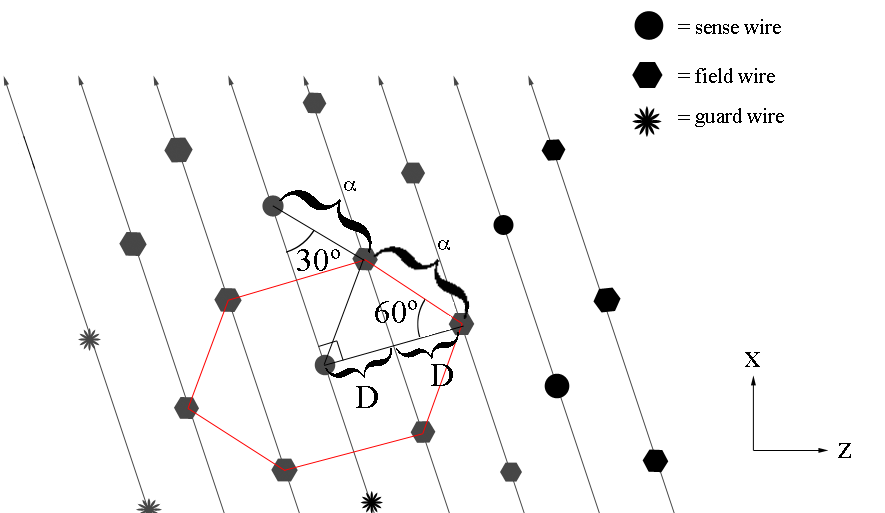
Since the separation between adjacent sense wires is uniform and at a set angle of 25 degrees with respect to the beam line, we can use this fact to determine the angle theta each wire makes when measured from the vertex.

$\Delta\ x=1.337\cos(25^{\circ})cm=1.212cm$

$\Delta\ z=-1.337\sin(25^{\circ})cm=-0.5652cm$

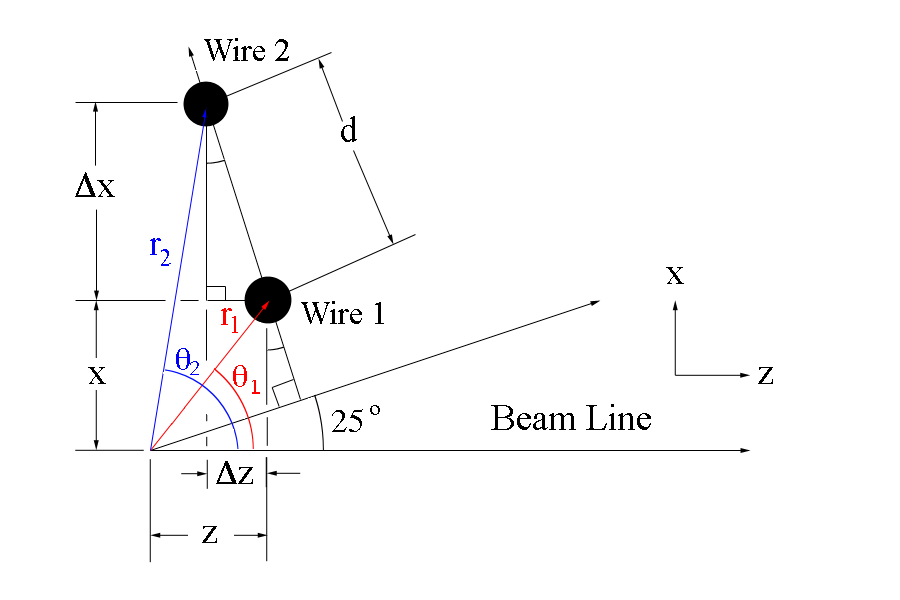
The new x and z coordinates for wire 2 can be found using the change in the components

$x'=x+\Delta x$ $z'=z+\Delta z$

This can be extended to any point along the same wire plane, starting from the coordinates for wire 1

$x'=x+\Delta x\times\ n$ $z'=z+\Delta z\times\ n$

The angle theta that the wire makes with the vertex is given by

$\tan{\theta}=\frac{x+\Delta x}{z+\Delta z}\Rightarrow \theta=\arctan{\frac{x+\Delta x}{z+\Delta z}}$

CED Verification

Using CED to verify the angle and wire correlation,

Zooming in on the view paralell to the direction of the wires in ced, we can examine the wire corresponding theta angle in the drift chamber.

Table 1: Superlayer 1 Wire 1 Coordinates

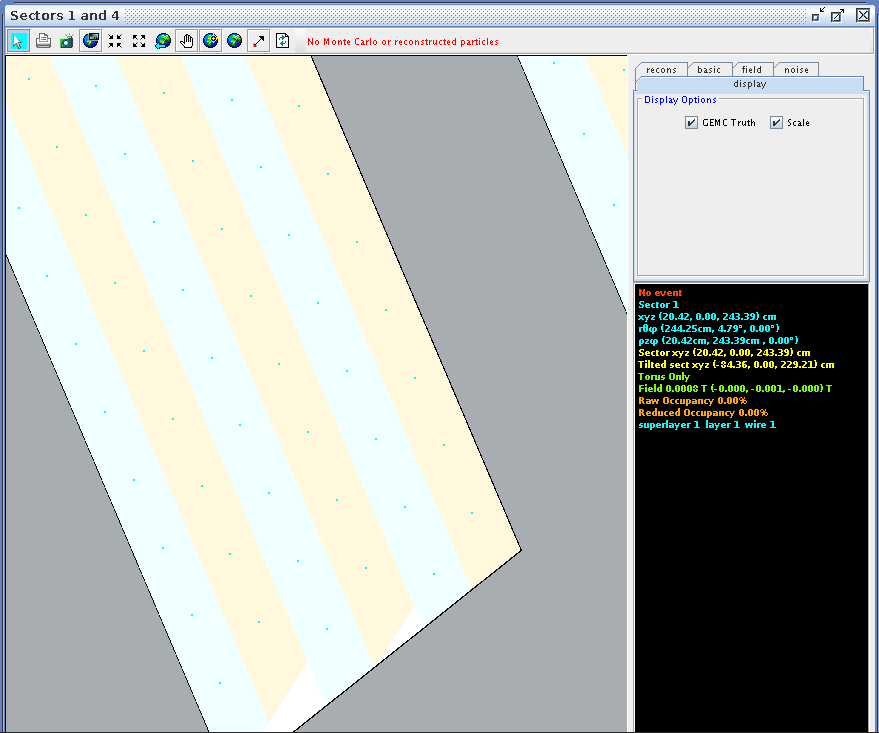
Coordinates(cm)	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5	Layer 6
x	20.42	21.51	21.39	22.49	22.37	23.47
y	0.00	0.00	0.00	0.00	0.00	0.00
z	243.41	244.18	245.51	246.28	247.62	248.38

Table 2: Superlayer 1 Wire 2 Coordinates

Coordinates(cm)	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5	Layer 6
x	21.64	22.73	22.61	23.71	23.58	24.69
y	0.00	0.00	0.00	0.00	0.00	0.00
z	242.86	243.62	244.94	245.71	247.05	247.81

Corresponding theta angles can be found for other wires, in Region 1, Superlayers 1 and 2.

Table 3: Superlayer 1 Wire-Angle Theta Correspondence in Degrees

Wire Number	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5	Layer 6
1	4.79	5.03	4.98	5.22	5.16	5.40
2	5.09	5.33	5.27	5.51	5.45	5.69
62	24.42
63	24.76
64	25.10
77	29.46	29.60	29.41	29.55	29.37	29.51
78	29.79	29.93	29.74	29.88	29.69	29.83
79	30.12	30.26	30.07	30.21	30.02	30.16
110	40.19	40.28	40.05	40.13	39.91	39.99
111	40.51	40.59	40.36	40.44	40.21	40.29
112	40.82	40.90	40.67	40.75	40.52	40.60

Table 4: Superlayer 2 Wire-Angle Theta Correspondence in Degrees

Wire Number	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5	Layer 6
1	4.79	5.03	4.98	5.22	5.16	5.40
2	5.09	5.33	5.27	5.51	5.45	5.69
77	29.46	29.60	29.41	29.56	29.37	29.51
78	29.79	29.93	29.74	29.88	29.70	29.84
79	30.13	30.27	30.07	30.21	30.02	30.16
110x	40.19	40.28	40.05	40.13	39.91	39.99
111	40.51	40.59	40.36	40.44	40.22	40.30
112	40.82	40.90	40.67	40.75	40.52	40.60

Super Layer 1:Layer 1

Table 1: Superlayer 1 Change of Coordinates From Wire 1 to Wire 2(cm)

Coordinates(cm)	Layer 1	Layer 2	Layer 3	Layer 4	Layer 5	Layer 6
$\Delta x$	1.22	1.22	1.22	1.22	1.21	1.22
$\Delta y$	0.00	0.00	0.00	0.00	0.00	0.00
$\Delta z$	.55	.56	.57	.57	.57	.57

Using the geometric construction for determining angle theta to wire 2:

$\tan{\theta}=\frac{x+\Delta x}{z+\Delta z}\Rightarrow \theta=\arctan{\frac{x+\Delta x}{z+\Delta z}}$

$\arctan{\frac{20.42+1.212}{243.39-0.5652}}=\arctan{\frac{21.632}{242.8248}}=\arctan{0.0891}=5.09^{\circ}$

This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.

$\tan{\theta}=\frac{x-\Delta x+n\Delta x}{z-\Delta z+n\Delta z}\Rightarrow \theta=\arctan{\frac{x'+n\Delta x}{z'+n\Delta z}}$

where

$x'=20.42-1.212\approx 19.21cm$ $z'=243.39+0.5652\approx 243.96cm$

$\theta=\arctan{\frac{19.21+n1.212}{243.39-n0.5652}}$

$\tan{\theta}=\frac{19.21+n1.212}{243.39-n0.5652}\Rightarrow \tan{ \theta}=-2.14437 + \frac{957.412}{430.626 - n}\Rightarrow 430.626 - n = \frac{957.412}{\tan{ \theta}+2.14437}$

$\Rightarrow n = \frac{-957.412}{\tan{ \theta}+2.14437}+430.626$

Using Mathematica, a series expansion about n=0 can be found:

In[1]:= Series[ArcTan[(19.21+1.212 x)/(243.39-0.5652 n)],{n,0,4}]

Out[1]= 0.0787635+0.00513098 n+9.83726*10^-6 n^2-2.61675*10^-8 n^3-2.22826*10^-10 n^4+O[n]^5

$\theta\approx 0.0787635+0.00513098 n+9.83726\times 10^{-6} n^2-2.61675\times 10^{-8} n^3$

This expression will find the angle theta in radians given the wire number. To convert from radians to degrees, we can multiply by 180 and divide by Pi.

In[2]:= 180*(0.07876354504106763`+0.005130982891104289` n+9.837257652182922`*^-6 n^2-2.616751708660921`*^-8 n^3-2.2282595631625944`*^-10 n^4+O[n]^5)/3.14159625359

Out[2]= 4.51281+0.293983 n+0.000563633 n^2-1.49929*10^-6 n^3-1.2767*10^-8 n^4+O[n]^5

$\theta\approx 4.51281+0.293983 n+0.000563633 n^2-1.49929\times10^{-6} n^3$

This tells us that the expression for theta will follow a function that comes from a series expansion. To account for instrument and measurement errors, angle measurements from ced can be used to find a better fit.

Using Mathematica, a line can be fitted to the data collected on the wire number to angle theta correspondence.

Declaring the data set:

In[1]:= data1={{1,4.79},{2,5.09},{62,24.42},{63,24.76},{64,25.10},{78,29.79},{111,40.50},{112,40.82}}

Out[1]= {{1,4.79},{2,5.09},{62,24.42},{63,24.76},{64,25.1},{78,29.79},{111,40.5},{112,40.82}}

Testing for a linear fit:

In[2]:= line1=Fit[data1,{1,n},n]

Out[2]= 4.39975 + 0.32469 n

Examing the range limits for the angle theta for layer 1:

Taking the difference of the upper and lower limits in theta,

$\Delta degrees=40.82^{\circ}-4.79^{\circ}=36.03^{\circ}$

Dividing by the change in wire numbers (112-1=111), we find

$\frac{\Delta degrees}{\Delta wire\ number}=\frac{36.03^{\circ}}{111\ wires}\approx\ \frac{0.325^{\circ}}{wire\ number}$

This would imply that if the wires were evenly placed, their change in angle theta would increase by the factor of .325 degrees for each increase in wire number, starting obviously with wire 1 at 4.79 degrees. In addition, this implies that the bin spacing for each wire would be around .325 degrees in width.

Chercking this, we can find the difference between wires 1 and 2,

$\frac{\Delta degree}{\Delta wire\ number}=\frac{5.09^{\circ}-4.79^{\circ} }{wire\ number}=\frac{.3^{\circ}}{wire\ number}$

Similarly, finding the difference between wires 111 and 112,

$\frac{\Delta degree}{\Delta wire\ number}=\frac{40.82^{\circ}-40.51^{\circ}}{wire\ number}=\frac{.31^{\circ}}{wire\ number}$

These differing values show that the bin width is not uniform in length, therefore a first order, linear fit, will not suffice.

Testing for a quadratic fit:

In[3]:= quad1=Fit[data1,{1,n,n^2},n]

Out[3]= 4.45564 +0.32015 n+0.0000417787 n^2

The quadratic fit does not work since it's first derivative

$\theta'\approx \Delta \theta=.325072-6.83308\ n$

does not give the same spacing between low and high values of n as seen in the ced data. The coefficient near the first order will have to smaller than .31 to find a correlation that would agree.

Testing for a polynomial of degree 3 fit:

In[4]:= polynomial1=Fit[data1,{1,n,n^2,n^3},n]

Out[4]= 4.49876 +0.293001 n+0.000679074 n^2-3.57132*10^-6 n^3

This fit best matches the data found in ced

$\theta\equiv 4.49876 +0.293001 n+0.000679074 n^2-3.57132\times 10^{-6} n^3$

As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number.

$\theta '\equiv 0.293001 + 0.00135815 n - 0.000010714 n^2$

The derivative of this function then will tell us where the bin spacing is at a minimum and a maximum.

$\theta ''\equiv .001021976-1.61514\times 10^{-5} n$

$0.00135815 - 0.0000214279 n=0\Rightarrow Bin\ Spacing\ Maximum\ at\ n=63.3822$

Comparing this maximum, we can see from Table 3 that near the maximum of 63 are seperated by larger distances than at n=1 or n=112. This is the midpoint of the plane as seen in the geometry file.

Binning based on wire numbers

The bin size based on wire number will need to be a uniform width of 1, as in an increment of 1 between the integer values of the wires. This uniformity in bin size based on wire numbers is not uniform when viewed by the angle theta due to the Drift Chamber geometry discussed earlier.

Modifying evioreader

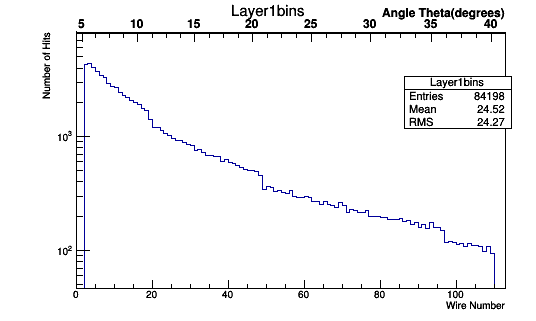
gStyle->SetStripDecimals(kTRUE);
TF1 *fit_function=new TF1("fit_function","[0]+[1]*x+[2]*x*x+[3]*x*x*x",4.49876,41.12592);
fit_function->SetParameters(4.49876,0.293001,0.000679074,-0.00000357132);
TGaxis *A1 = new TGaxis(0,5000,113,5000,"fit_function",510,"-");
A1->SetTitle("Angle Theta(degrees)");
A1->Draw();

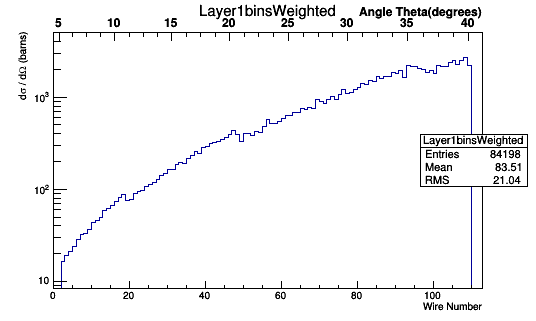
Using the expression for n in terms of Theta:

$n = \frac{-957.412}{\tan{ \theta}+2.14437}+430.626$

This relationship can be used to multiply each Moller Scattering angle theta in the lab frame, with it's differential cross-section weight, to find the Moller differential cross-section as a function of wire number in the lab frame.

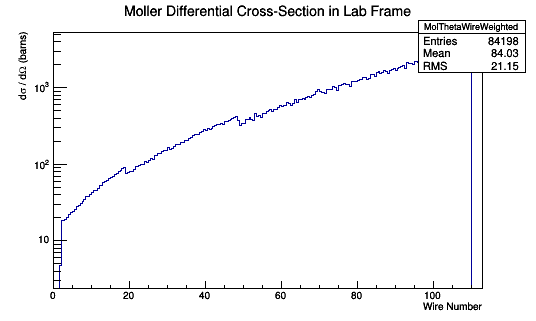
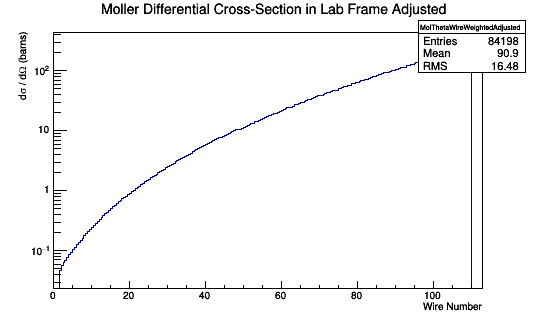
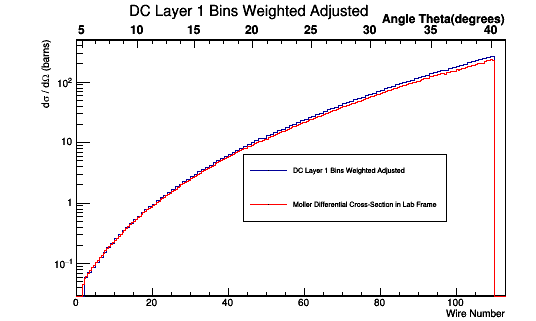
Moller Occupancy Rate

Comparing Rates

Using the values from Whitney:

For a 5cm target of LH2:

$\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6.022\times10^{23} molecules\ LH_2}{1 mole} \frac{2 atoms}{1\ molecule\ LH_2} \times \frac{1m^3}{(100 cm)^3} \times \frac{5 cm}{ }=2.11\times 10^{23} \times \frac{10^{-24} cm^{2}}{barn}=2.11\times 10^{-1}\ barns^{-1}$

Using the beam current of 100nA,

$\Phi_{beam}=\frac{100\times 10^{-9}\ A}{1} \times \frac{1\ C}{1\ A} \times \frac{1\ e^{-}}{1\ s} \times \frac{1}{1.602\times 10^{-19}C}\Rightarrow 6.2422\times 10^{11}\ \frac{1}{s}=\Phi_{e^{-}}$

Given the beam Luminosity of:

$\mathcal {L}=\frac{1.32\times 10^{35}}{cm^2 \cdot s}\frac{10^{-24} cm^{2}}{barn}=\frac{1.32\times 10^{11}}{barn\cdot s}=\Phi_{beam}\ \rho\ l_{target}$

We can check to make sure the density makes sense

$\Rightarrow \rho_{target}=\frac{1.32\times 10^{35}}{ \Phi_{beam}\ l_{target}cm^2 \cdot s}=\frac{1.32\times 10^{35}}{ 6.24\times 10^{11}\ \cdot 5cm^3}=\frac{4.23\times 10^{22}}{cm^3}$

$\Rightarrow \rho_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6.022\times10^{23} molecules\ LH_2}{1 mole} \times \frac{1m^3}{(100 cm)^3}\frac{2 atoms}{1\ molecule\ LH_2}=\frac{4.23\times 10^{22}}{cm^3}$

Using the values from Whitney :

https://wiki.iac.isu.edu/index.php/CLAS12_RateEst_byWA

Rates

Energy	6 GeV	11 GeV
Process	(nb)	(nb)
Moller	22773001	75008636
DIS + radiative tail	128	83
Elastic e-p	5511220	3670740
Elastic radiative tail	24705	12944
π0 electro-production	14802	17908
π0 photo-production	569	852
π+ electro-production	4032	5536
π+ photo-production	282	487
π− electro-production	2806	3843
π− photo-production	199	342
Total	2.83317E7	7.87214E7

$R_{Total\ scattered}= \sigma_{Total\ scattered} \mathcal{L}=7.87\times 10^{-2}\ barn\ \cdot \frac{1.33\times 10^{11}}{barn\cdot s}=\frac{1.05\times 10^{10}Total Scattered}{s}$

$R_{Moller}= \sigma_{Moller} \mathcal{L}=7.50\times 10^{-2}\ barn\ \cdot \frac{1.33\times 10^{11}}{barn\cdot s}=\frac{9.97\times 10^{9}Moller}{s}$

Similarly,

$N_{Total\ scattered} =R_{Total\ scattered}\cdot t$

$N_{Moller} =R_{Moller}\cdot t$

File:CLAS12ExpWS WA.pdf

$\sigma=\frac{R}{\mathcal{L}}=\frac{dN}{dt}\cdot \frac{1}{\mathcal{L}}$

$\Rightarrow \int\limits_{0}^{t}\, dt=\int\limits_{0}^{N}\frac{1}{\sigma \mathcal{L}}\, dN$

$t_{Total\ scattered}=\frac{N_{Total\ scattered}}{\sigma_{Total\ scattered} \Phi \rho \ell}=\frac{1000000\ barn \cdot s}{7.87\times 10^{-2} \cdot 1.33\times 10^{11}\ barn}=9.54\times 10^{-5} s$

$N_0=\Delta t \cdot R_{Total\ scattered}=\Delta t \cdot \frac{N_{Total\ scattered}}{t_{Total\ scattered}}=500\times 10^{-9}\ s \cdot \frac{1\times 10^6}{0.0954\times 10^{-3}\ s}=5240$

$Occupancy=\frac{N_{Hits}}{N_0}=\frac{N_{Hits}}{\Delta t \cdot R_{Total\ scattered}}=\frac{t_{Total\ scattered}\cdot N_{Hits}}{N_{Total\ scattered}\cdot \Delta t}=$

$\left ( \frac{Number\ of\ hits}{Moller\ electron}\right ) \left (\frac{Moller\ electrons}{incidents\ electron} \right) \left (\frac{incident\ electrons}{sec} \right )$

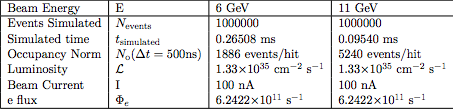
GEANT Simulations

https://wiki.iac.isu.edu/index.php/Converting_to_barns

https://wiki.iac.isu.edu/index.php/Check_Differential_Cross-Section

Converting the number of electrons scattered per angle theta to barns, we can use the relation

$\mathcal{L}=\frac{R_{scattered}}{\sigma} = \Phi_{beam}\ \rho\ \ell$

$\sigma=\frac{R_{scattered}}{\mathcal{L}} =\frac{R_{scattered}}{\Phi_{beam}\ \rho\ \ell}= \frac{R_{scattered}}{R_{incident}\ \rho\ \ell}=\frac{N_{scattered}}{\Delta t}\cdot \frac{\Delta t}{N_{incident}}\cdot \frac{1}{\rho \ell}$

This gives, for LH2:

$\rho_{target}\times l_{target}=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} molecule}{1 mole} \times \frac{2\ atoms}{molecule}\times \frac{1m^3}{(100 cm)^3} \times \frac{1 cm}{ } \times \frac{10^{-24} cm^{2}}{barn} =4.2\times 10^{-2} barns^{-1}$

Since the time window must be the same for the amount scattered as for the amount incident, this can be viewed as the probablity of one incident electron producing a Moller event.

From earlier simulations for random angle Phi, we know that the full range of Theta is limited depending on the target material.

$\sigma=\frac{N_{scattered}}{\mathcal{L}} = \frac{N_{scattered}}{N_{incident}\ \rho\ \ell}=\frac{975593}{40000000\ \cdot 4.2\times 10^{-2} barns^{-1}}=\frac{0.024}{4.2\times 10^{-2} barns^{-1}}=0.58 barns$

$\sigma=\frac{N_{scattered}}{\mathcal{L}} \Rightarrow \mathcal{L}=\frac{N_{scattered}}{\sigma}$

$\mathcal{L}=\frac{975593}{0.58 barns}=1.68\times 10^{6}\frac{electrons}{barn \cdot s}$

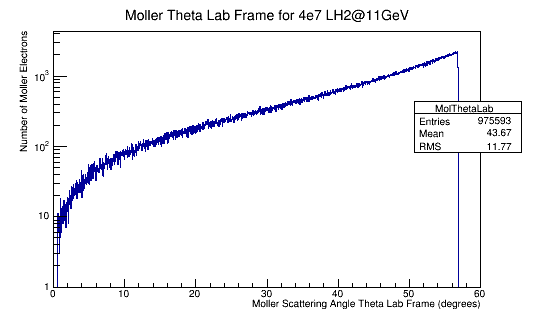
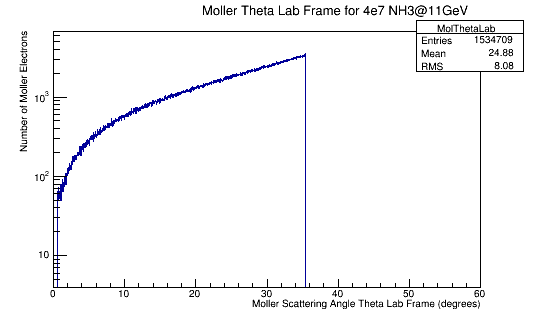
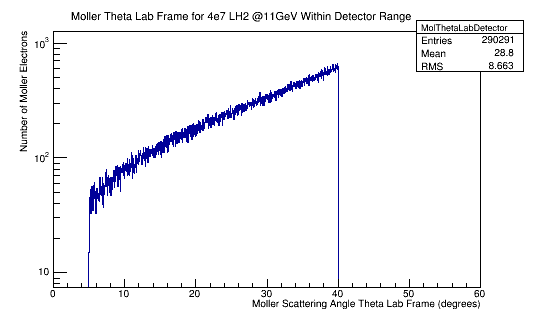
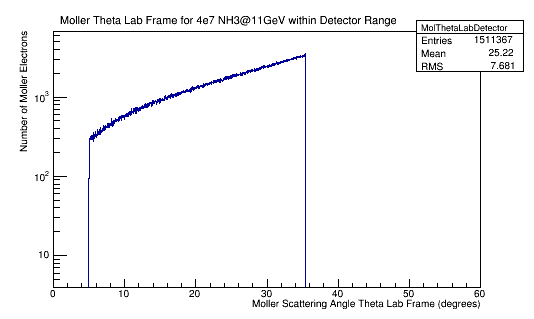
Moller events occur for about 2.5% of the incident electrons on a LH2 target. We can assume the number of Moller events that occur within the DC range to be around 30% of the total Moller events occuring for the number of incident electrons for LH2 as well. Since the differential cross-section over the angel theta is proportional to the differtial cross-section over wire number we can dividing the Moller differential cross-section by the product of the density and length of the target material

Isotropic Weighted Distribution

Assuming a 1cm long target of LH2 where around 2% of the incident electrons will result in a Moller electron,

TH1F *Combo=new TH1F("Layer1binsMollerRate","Layer1binsMollerRate",113,0,113);
Combo->Add(Layer1binsWeighted,23.8);
Combo->Draw();

$\frac{2003912\ Moller\ Events\ in\ Range}{.30\ Moller\ Events\ in\ Range\ per\ Moller\ Electron}=6.68\times 10^6\ Moller\ electrons$

$\frac{6.68\times 10^6\ Moller\ electrons}{.02\ Moller\ Events\ \ per\ Incident\ Electron}=3.34\times 10^8\ Incident\ electrons$

$\sigma=\frac{N_{Moller}}{N_{incident}\cdot \rho \ell}=\frac{.02\ barn}{4.2\times 10^{-2}}=.48\ barn$

$\mathcal{L}=N_{incident}\ \rho \ell=3.34\times 10^8\ Incident\ electrons \cdot 4.2\times 10^{-2}=\frac{1.40\times 10^{7}\ electrons}{barn \cdot s}$

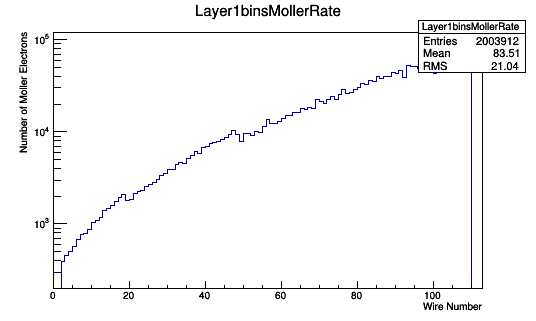
Assuming a 5cm long target of LH2 where around 2% of the incident electrons will result in a Moller electron,

TH1F *Combo=new TH1F("Layer1binsMollerRate","Layer1binsMollerRate",113,0,113);
Combo->Add(Layer1binsWeighted,4.76);
Combo->Draw();

$\frac{400782\ Moller\ Events\ in\ Range}{.30\ Moller\ Events\ in\ Range\ per\ Moller\ Electron}=1.34\times 10^6\ Moller\ electrons$

$\frac{1.34\times 10^6\ Moller\ electrons}{.02\ Moller\ Events\ \ per\ Incident\ Electron}=6.67\times 10^7\ Incident\ electrons$

$\sigma=\frac{N_{Moller}}{N_{incident}\cdot \rho \ell}=\frac{.02\ barn}{2.1\times 10^{-1}}=.095\ barn$

$\mathcal{L}=N_{incident}\ \rho \ell=6.67\times 10^7\ Incident\ electrons \cdot 2.1\times 10^{-1}=\frac{1.40\times 10^{7}\ electrons}{barn \cdot s}$