Initial rate study

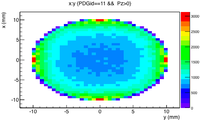
2mm thick PbBi, 10 MeV, 1 cm cylindrical incident electron distribution

G4beamline pencil beam 10 cm radius

beam ellipse particle=e- nEvents=1000000 beamZ=0.0 beamX=0. beamY=0. \
        sigmaX=10.0 sigmaY=10.0 sigmaXp=0.000 sigmaYp=0.000 \
      meanMomentum=10. sigmaE=0. maxR=10.

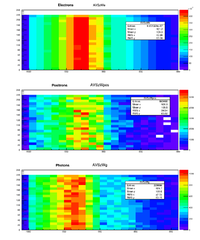
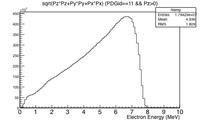
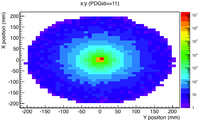
Incident Electron spatial distribution and energy

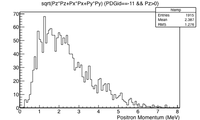
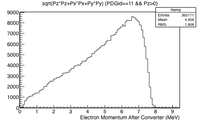
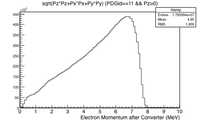
Positron and Electron Momentum after the converter

PbBi Thickness (mm)	#positrons/million electrons (G4Beamline)	#positrons/million electrons (MCNPX)
1	1169,1083,1068,1090,1088 =1100[math]\pm[/math] 40	1091
1.5	1723, 1668,1671, 1687,1726=1695[math]\pm[/math] 28	1728
2	1902,1921,1886,1967,1922=1920[math]\pm[/math] 30	1984
3	1920,1880,1883,1864,1857=1881 [math]\pm[/math] 24	1986
4	1688, 1766, 1712, 1709, 1753=1726[math]\pm[/math] 33	1858
5	1569,1585,1509 ,1536,1551=1550[math]\pm[/math] 29	1646
7	1475,1450,1457,1428,1477 =1457[math] \pm[/math] 20	1541
10	1250,1180,1178,1186,1166=1192[math]\pm[/math] 33	1216

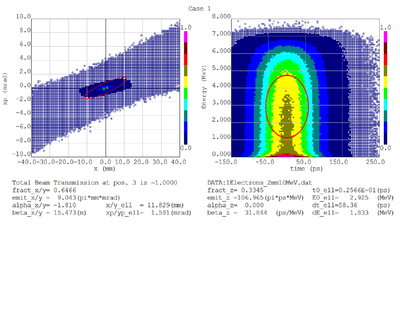
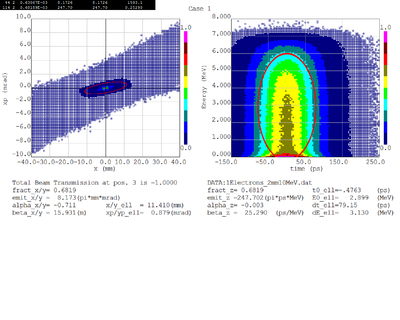
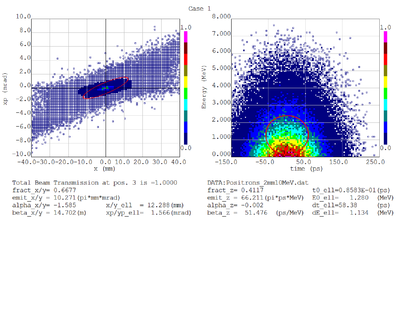
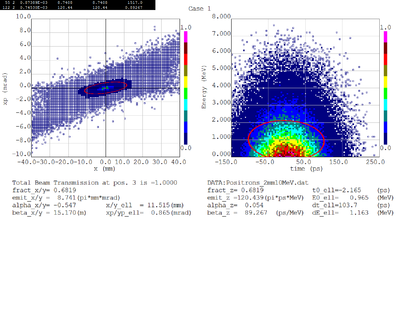
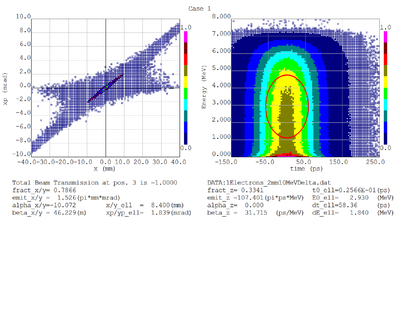
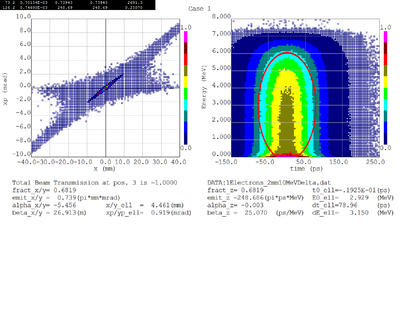
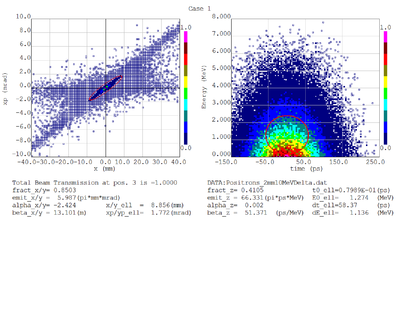
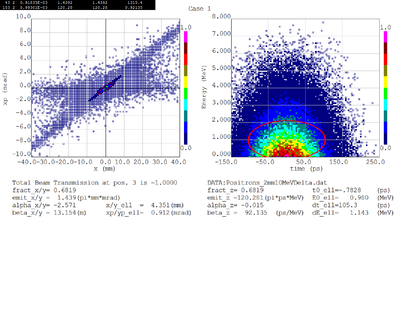
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:

1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")

2. Twiss parameters

3. Ellipse centroid for longitudinal phase portrait

4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.

Electrons - RMS

Electrons - 68.2% core

Positrons - RMS

Positrons - 68.2% core

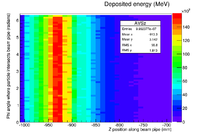
The plot below shows the energy deposited in MeV along the pipe. The Z axis is along the beam direction. The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe. The bins are 1cm x 1cm.

A maximum of 450,000 MeV is deposited in a 1 cm[math]^2[/math] bin when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.

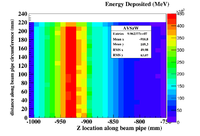
Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.

Why is the positron hotspot upstream of the target? Because beam was going from right to left.

root commands used

TH2D *AVSz=new TH2D("AVSz","AVSz",100,-1000,0,12,-60,60)
BeamPipeE->Draw("35.*atan(PosYmm/PosXmm):PosZmm>>AVSz","DepEmeV"); 
AVSz->Draw("colz");

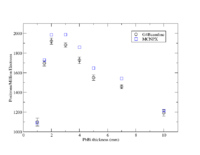
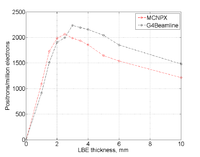
Rate comparison with Energy and target thickness

Difference with above simulation are that GEANT4 has SS windows and all created positrons that leave the target are counted , not just those going through a Sensitive detector downstream

6MeV

PbBi Thickness (mm)	#positrons/million electrons (GEANT4.9.6.p02	#positrons/million electrons (G4Beamline)
0.5	284,306,281,290,288 = 290[math]\pm[/math]10
1	465,449,457,454,472 = 459[math]\pm [/math]9
1.5	456,416,445,445,434 =439[math]\pm [/math]15
2	396,418,394,415,395 =404[math]\pm [/math]12
4	338,327,332,341,336=335[math]\pm [/math]5
7	257,280,265,268,259 =266[math] \pm [/math]9
10	223,225,234,210,221 =223[math]\pm[/math] 9

8 MeV

PbBi Thickness (mm)	#positrons/million electrons (GEANT4.9.6.p02	#positrons/million electrons (G4Beamline)
0.5	458,458,535,533,516=500 [math]\pm [/math]39
1	994,996,967,971,956=977[math] \pm [/math]18
1.5	1166,1196,1139,1176,1178=1171[math]\pm[/math] 21
2	1184,1212,1175,1194,1178=1189[math]\pm[/math] 15
4	989,1013,975,962,956= 979[math]\pm[/math]23
7	815,765,829,806,817=806[math] \pm[/math] 25
10	641,660,636,671,682 = 658[math]\pm[/math]20

10 MeV

PbBi Thickness (mm)	#positrons/million electrons (GEANT4.9.6.p02	#positrons/million electrons (G4Beamline)
0.5	628,653,713,686,689 = 674[math]\pm[/math]33
1	1524,1607,1565,1598,1581 = 1575 [math]\pm[/math] 33
1.5	2163,2264,2091,2154,2094= 2153[math]\pm[/math] 70
2	2445,2386,2321,2359,2368 = 2376 [math]\pm[/math] 45
4	2087,2104,2121,2154,2118 = 2117 [math]\pm[/math] 25
7	1675,1697,1708,1720,1750=1710 [math] \pm[/math] 28
10	1398,1421,1374,1418,1398 = 1402[math]\pm[/math] 19

Use Gaussian to make a incident uniform beam that is 1 cm in diameter and has a beam sigma of 1 cm , then cut out the beam to have a 0.5 cm circular radius.

First simple test is to send 1 million, 10 MeV electrons towards a PbBi target and count how many positrons leave the downstream side

The Random number seed is set by Time in G4beamline to use a different set of pseudo random numbers each time it is run

The G4Beamlin incident electron beam has the following properties

beam gaussian particle=e- nEvents=1000000 beamZ=0.0 
        sigmaX=1.0 sigmaY=1.0 sigmaXp=0.100 sigmaYp=0.100 
        meanMomentum=10.0 sigmaP=4.0 meanT=0.0 sigmaT=0.0

-

PbBi Thickness (mm)	#positrons/million electrons (G4Beamline)	#positrons/million electrons (MCNPX)
1	960,874, 916,934,897=916 +/- 33	1091
1.5	1508	1728
2	1963,1919,1880,1877,1970 = 1902 [math]\pm[/math] 43	1984
2.5	1997	2062
3	2233,2250, 2251,2226 , 2222=2236 [math]\pm[/math] 13	1986
3.5	2193	1938
4	2184,2156,2089,2173,2181=2157 [math]\pm[/math] 39	1858
5	2042	1646
6	1851, 1932, 1857, 1896,1924 = 1892[math] \pm[/math] 37	1541
10	1480,1488	1216

Comparison of G4Beamline and MCNPX

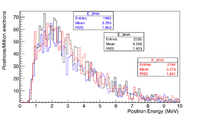
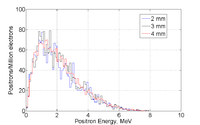
Energy Distribution

Angular distribution of positrons

I was unable to do anything other than a gaussian beam right now, I will try to do one later

For now I have a gaussian with an 8mm RMS and 10 MeV incident electrons as shown below.

The positron and electron momentum distributions after the PbBi converter are shown below

A comma delimited text file with the above events in the format of

x,y,z,Px,Py,Pz

in units of cm for distance and MeV for momentum is located at

for positrons

http://www2.cose.isu.edu/~foretony/Positrons_2mm10MeV.dat

and

http://www2.cose.isu.edu/~foretony/Electrons_2mm10MeV.dat

for electrons

For now I have a gaussian with an 1mm RMS and 10 MeV incident electrons as shown below.