DV RunGroupC Moller
need to insert moller shielding into card after moller LUND file is created. (see clas12/beamline)
Simulating the Moller scattering background for EG12
GEANT4 Simulation of Moller Events
Simulation Setup
Determine the Moller background using an LH2 target to check the physics in GEANT4
Detector Material and Construction
Using GEANT4, the ExampleN02 file was edited to run for a NH3 target. The file ExN02DetectorConstruction.cc was edited with
//--------- Material definition ---------
G4double a, z;
G4double density, temperature, pressure;
//Liquid Hydrogen
G4Material* LH2 = new G4Material("Hydrogen", z=2., a=2.02*g/mole, density=0.07*g/cm3, kStateGas,3*kelvin,1.7e5*pascal);
The target is a cylinder with a 1.5 cm diameter and 1 cm thickness following dimensions listed on page 8 of File:PHY02-33.pdf
//--------- Sizes of the principal geometrical components (solids) --------- NbOfChambers = 1; ChamberWidth = 1.5*cm; ChamberSpacing = 40*cm; fTrackerLength = (NbOfChambers+1)*ChamberSpacing; // Full length of Tracker fTargetLength = 1.0 * cm; // Full length of Target TargetMater = NH3; ChamberMater = BadVacuum; //fWorldLength= 1.2 *(fTargetLength+fTrackerLength); fWorldLength= 1.2 *(10+fTrackerLength)+100 *cm; G4double targetSize = 0.5*fTargetLength; // Half length of the Target G4double trackerSize = 0.5*fTrackerLength; // Half length of the Tracker
Recording Moller Events
Moller scattering does not have a GEANT4 specific setting, so the file ExN02SteppingVerbose.cc was edited to record only events that would correspond to Moller events. Since Moller scattering is simply electron-electron scattering, we can look for events where electron ionization is the process in the data stream. We will limit this to only particles with a parentID of 0 and 1 representing the parent and daughter (Moller) electrons. This eliminates second generation Moller scatterings, which only ocur about 2 times out of 1E6 incoming electrons. This method also eliminates Delta Rays or Knock-on-Electrons.
The file ExN02SteppingVerbose.cc is read for each step in the GEANT4 simulation, so recording the momentum, position, and energies of the electrons before and after the collision can be found in multiple loops.
On the first pass of SteppingVerbose, the data is recorded into a temporary variable set. The physical process of ionization occurs after the collision of the two electrons. This implies that the data could possible be the initial state of the incoming electron. This is read every time to be prepared for the subsequent pass where the process of ionization (scattering) is active.
void ExN02SteppingVerbose::StepInfo()
{
.
.
.
if(fTrack->GetDefinition()->GetPDGEncoding()==11 && fStep->GetPostStepPoint()->GetProcessDefinedStep()->GetProcessName()!="eIoni" && fTrack->GetParentID()==0)
{
Temp_Energy=fTrack->GetKineticEnergy();
Temp_Mom_x=fTrack->GetMomentum().x();
Temp_Mom_y=fTrack->GetMomentum().y();
Temp_Mom_z=fTrack->GetMomentum().z();
Temp_Pos_x=fTrack->GetPosition().x();
Temp_Pos_y=fTrack->GetPosition().y();
Temp_Pos_z=fTrack->GetPosition().z();
}
On a pass afterwards, the data is read into a variable for the final state when the physical state is ionization, representing the Moller scattering. The the temporary variable is read into the initial state.
if( fTrack->GetDefinition()->GetPDGEncoding()==11 && fStep->GetPostStepPoint()->GetProcessDefinedStep()->GetProcessName()=="eIoni" && fTrack->GetParentID()==0)
{
Final_Energy= fTrack->GetKineticEnergy();
Final_Mom_x=fTrack->GetMomentum().x();
Final_Mom_y=fTrack->GetMomentum().y();
Final_Mom_z=fTrack->GetMomentum().z();
Final_Pos_x=fTrack->GetPosition().x();
Final_Pos_y=fTrack->GetPosition().y();
Final_Pos_z=fTrack->GetPosition().z();
Init_Energy=Temp_Energy;
Init_Mom_x=Temp_Mom_x;
Init_Mom_y=Temp_Mom_y;
Init_Mom_z=Temp_Mom_z;
Init_Pos_x=Temp_Pos_x;
Init_Pos_y=Temp_Pos_y;
Init_Pos_z=Temp_Pos_z;
}
This will write the data to an external file only for a 1st generation daughter particle and an active trigger. Afterwards, the trigger is turned off so that the recording process can start again.
if(fTrack->GetDefinition()->GetPDGEncoding()==11 && fTrack->GetParentID()==1 && trigger==1 )
{
outfile
//G4cout
<< Init_Energy<< " "
<< Init_Mom_x << " "
<< Init_Mom_y << " "
<< Init_Mom_z << " "
<< Init_Pos_x << " "
<< Init_Pos_y << " "
<< Init_Pos_z << " "
<< Final_Energy << " "
<< Final_Mom_x << " "
<< Final_Mom_y << " "
<< Final_Mom_z << " "
<< Final_Pos_x << " "
<< Final_Pos_y << " "
<< Final_Pos_z << " "
<< Mol_Energy << " "
<< Mol_Mom_x << " "
<< Mol_Mom_y << " "
<< Mol_Mom_z << " "
<< Mol_Pos_x << " "
<< Mol_Pos_y << " "
<< Mol_Pos_z << " "
<< G4endl;
trigger=0;
}
.
.
.
}
On a later pass, the condition that the parentID no longer represents the parent. This implies that the particle a Moller electron and the data is recorded into the Moller final state. The trigger is activated, which on the next pass of the program will allow a printout of all Moller Scattering data.
void ExN02SteppingVerbose::TrackingStarted()
{
.
.
.
if(fTrack->GetDefinition()->GetPDGEncoding()==11 && fTrack->GetParentID()>0)
{
Mol_Energy=fTrack->GetKineticEnergy();
Mol_Mom_x=fTrack->GetMomentum().x();
Mol_Mom_y=fTrack->GetMomentum().y();
Mol_Mom_z=fTrack->GetMomentum().z();
Mol_Pos_x=fTrack->GetPosition().x();
Mol_Pos_y=fTrack->GetPosition().y();
Mol_Pos_z=fTrack->GetPosition().z();
trigger=1;
}
.
.
.
}
Working with Moller Data
The event data from the GEANT4 simulation is written to a data file in the following format:
|- ! KEi ! Pxi ! Pyi ! Pzi ! xi ! yi ! z1 ! KEf ! Pxf ! Pyf ! Pzf ! xf ! yf ! zf ! KEm ! Pxm ! Pym ! Pzm ! xm ! ym ! zm |- | 11000 | 0 | 0 | 11000.5 | 0 | 0 | -510 | 10999.1 | 0.433025 | -0.858867 | 10999.6 | 0 | 0 | -509.276 | 0.905324 | -0.433025 | 0.858867 | 0.905366 | 0 | 0 | -509.276
|}Where each line represents a Moller scattering with the kinematic variables of kinetic energy, Momentum in the x, y, and z directions, as well as the x, y, and z position of the collision for the Incoming electron, the scattered state of the incoming electron, and the scattered Moller electron in that specific order.
Using a c++ macro, the variables are read into a Root tree, with branches for each variable. Specific histograms are also created for the total momentum and the scattering angle theta for the scattered and Moller electron, both in the Lab frame and Center of Mass frame.
tree->Branch("evt",&evt.event,"event/I:IntKE/F:IntPx:IntPy:IntPz:IntPosx:IntPosy:IntPosz:FnlKE:FnlPx:FnlPy:FnlPz:FnlPosx:FnlPosy:FnlPosz:
MolKE:MolPx:MolPy:MolPz:MolPosx:MolPosy:MolPosz");
while(in.good())
{
//Create Tree from GEANT4 simulation data
evt.event=nlines;
in >> evt.IntKE >> evt.IntMom[0] >> evt.IntMom[1] >> evt.IntMom[2] >> evt.IntPos[0]
>> evt.IntPos[1] >> evt.IntPos[2] >> evt.FnlKE >> evt.FnlMom[0] >> evt.FnlMom[1] >> evt.FnlMom[2]
>> evt.FnlPos[0] >> evt.FnlPos[1] >> evt.FnlPos[2] >> evt.MolKE >> evt.MolMom[0] >> evt.MolMom[1]
>> evt.MolMom[2] >> evt.MolPos[0] >> evt.MolPos[1] >> evt.MolPos[2];
nlines++;
tree->Fill();
FnlE=sqrt(evt.FnlMom[0]*evt.FnlMom[0]+evt.FnlMom[1]*evt.FnlMom[1]+evt.FnlMom[2]*evt.FnlMom[2]+0.511*0.511);
IntE=sqrt(evt.IntMom[0]*evt.IntMom[0]+evt.IntMom[1]*evt.IntMom[1]+evt.IntMom[2]*evt.IntMom[2]+0.511*0.511);
MolE=sqrt(evt.MolMom[0]*evt.MolMom[0]+evt.MolMom[1]*evt.MolMom[1]+evt.MolMom[2]*evt.MolMom[2]+0.511*0.511);//Define 4Vectors
Fnl4Mom.SetPxPyPzE(evt.FnlMom[0],evt.FnlMom[1],evt.FnlMom[2],FnlE);
Int4Mom.SetPxPyPzE(evt.IntMom[0],evt.IntMom[1],evt.IntMom[2],IntE);
Mol4Mom.SetPxPyPzE(evt.MolMom[0],evt.MolMom[1],evt.MolMom[2],MolE);
//Create Lab Frame Histograms
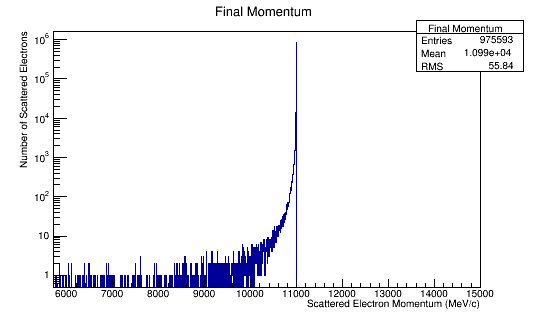
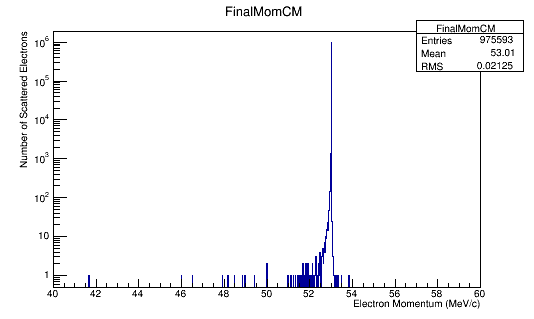
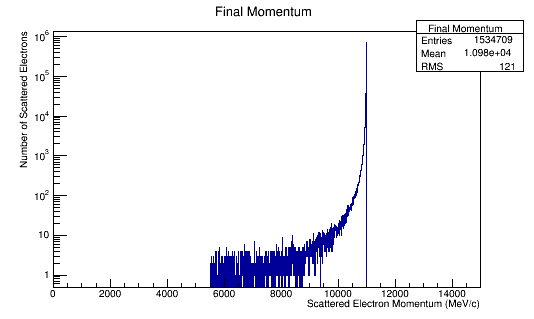
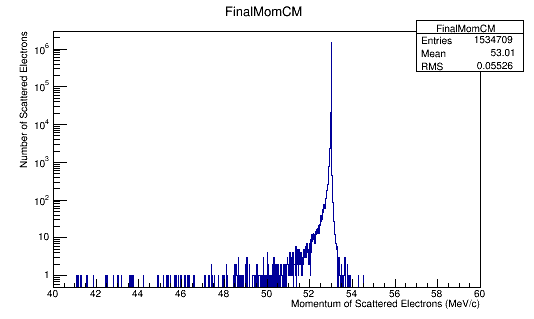
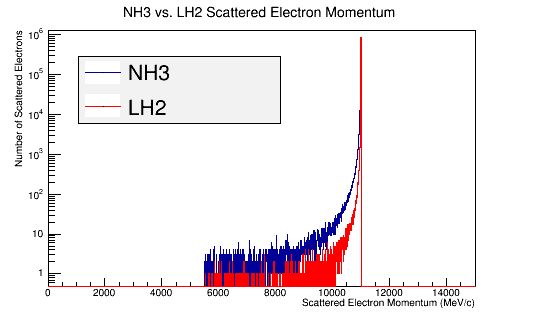
FinalMomentum->Fill(Fnl4Mom.P());
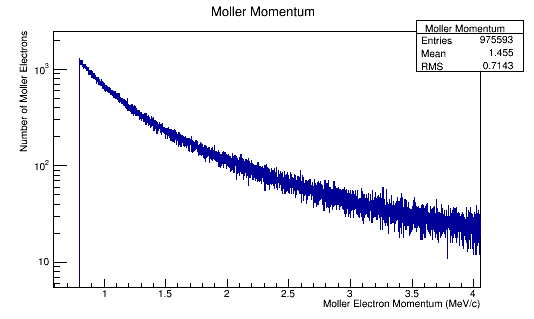
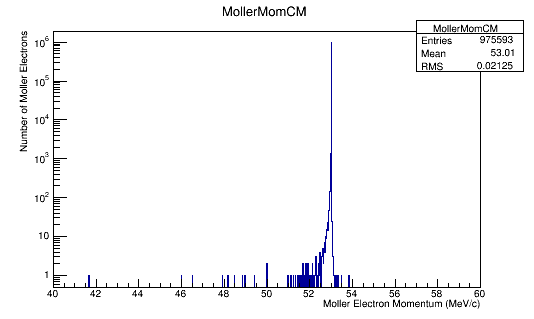
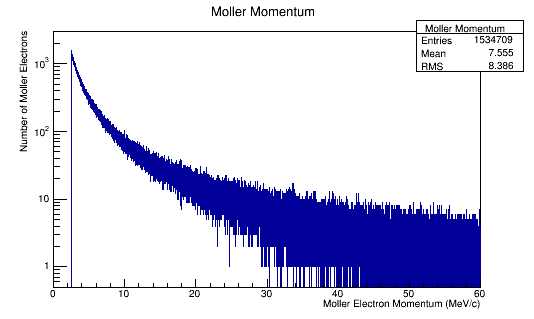
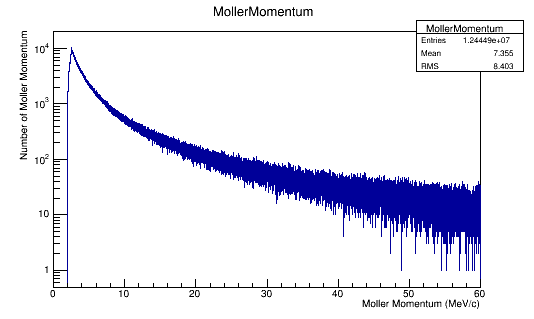
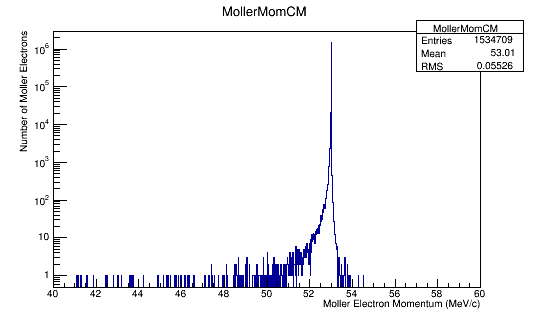
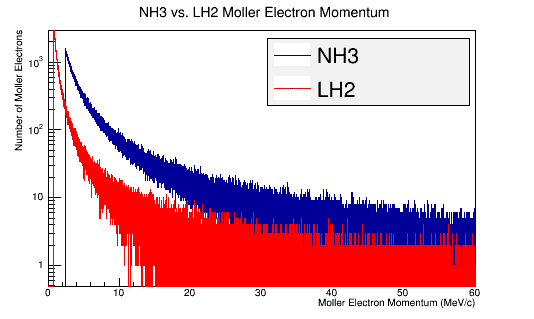
MollerMomentum->Fill(Mol4Mom.P());
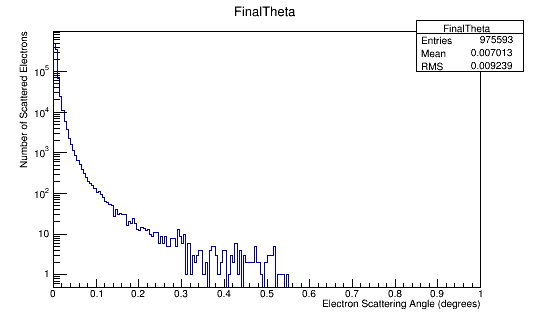
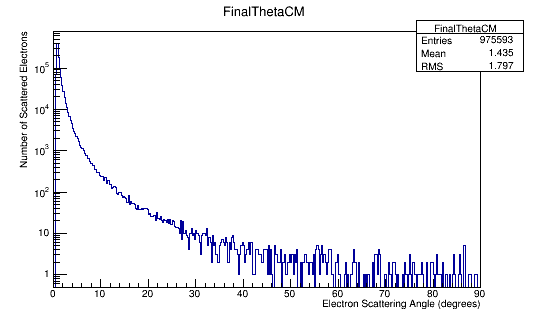
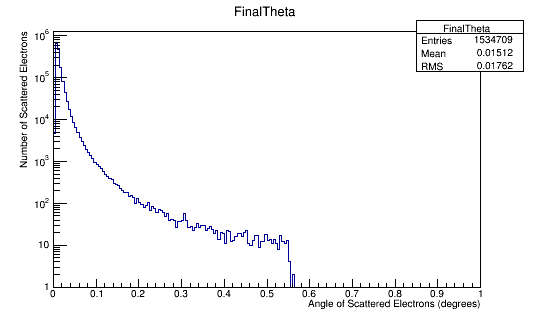
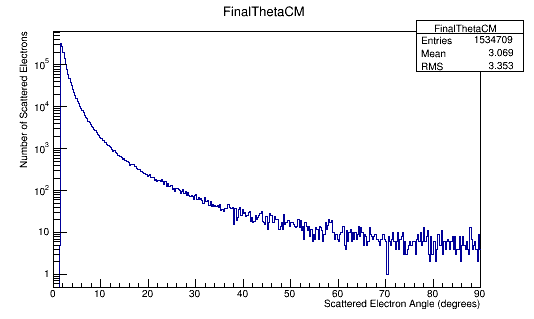
FinalTheta->Fill(Fnl4Mom.Theta()*180/3.14);
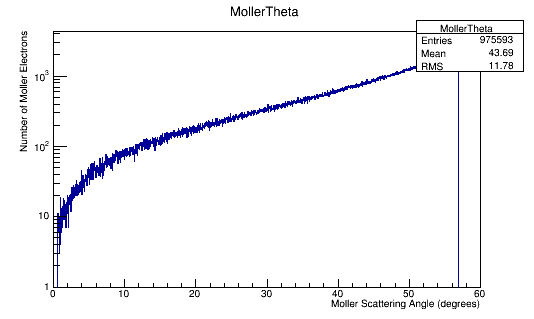
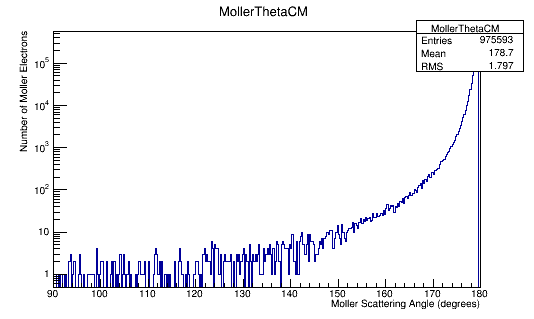
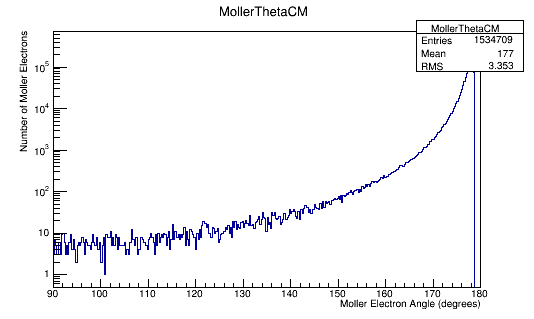
MollerTheta->Fill(Mol4Mom.Theta()*180/3.14);
//Boost to Center of Mass Frame
CMS=Fnl4Mom+Mol4Mom;
Fnl4Mom.Boost(-CMS.BoostVector());
Mol4Mom.Boost(-CMS.BoostVector());
//Create CM Histograms
FinalMomentumCM->Fill(Fnl4Mom.P());
MollerMomentumCM->Fill(Mol4Mom.P());
FinalThetaCM->Fill(Fnl4Mom.Theta()*180/3.14);
MollerThetaCM->Fill(Mol4Mom.Theta()*180/3.14);
}
'Momentum distributions in the Lab Frame
Angular Distribution in the Lab Frame
Momentum distributions in the Center of Mass Frame
Estimated Momentum Distribution
Noting that the GEANT4 data included data for the Kinetic Energy and not the total energy, we can perform the substitution using
Performing the relativistic transformation, we find for an incoming electron with momentum of 11GeV, we should find the momentum in the center of mass to be around 53 MeV .
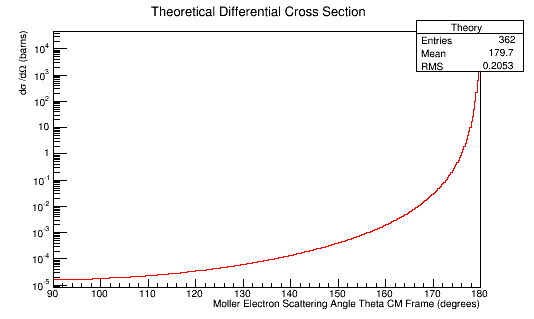
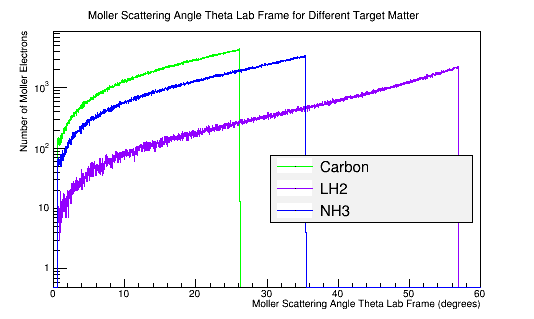
Angular Distribution in the Center of Mass Frame
Comparing experimental vs. theoretical for Møller differential cross section 11GeV
Using the equation from [1]
This can be simplified to the form
Plugging in the values expected for a scattering electron:
Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around
Using the conversion of
The trigonometric function part of the equation comes out to it's minimum of 9 at 90 degrees.
We find that the differential cross section scale is
Converting the number of electrons to barns,
where ρtarget is the density of the target material, ltarget is the length of the target, and iscattered is the number of incident particles scattered.
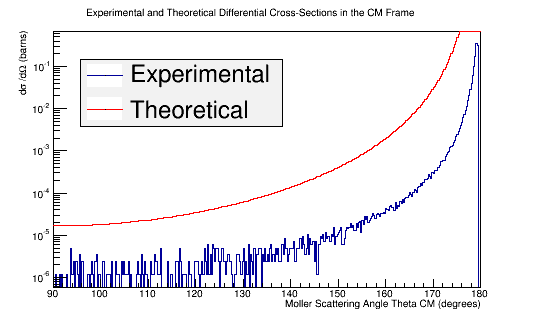
Combining these plots, and rescaling the Moller Scattering Angle Theta in the Center of Mass for barns, we find
TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
Combo->Add(MollerThetaCM,1.19e-6);
Combo->Draw();
Theory->Draw("same");
Step 2
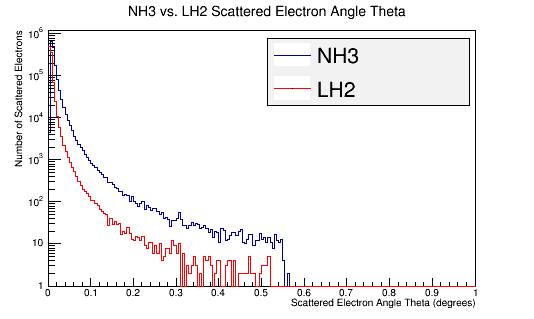
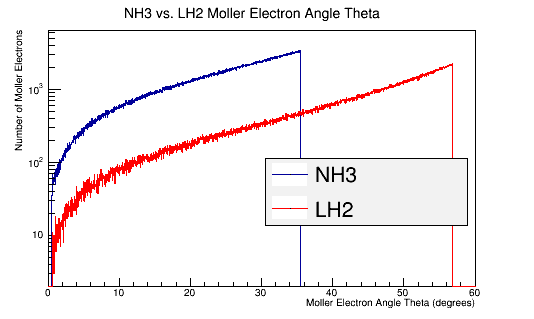
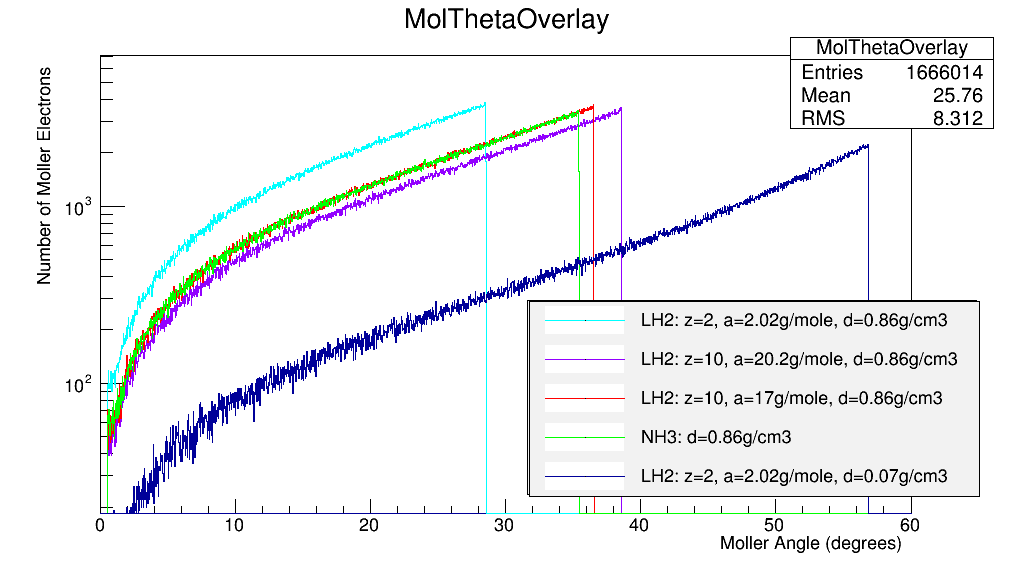
Replace the LH2 target with an NH3 target and compare with LH2 target.
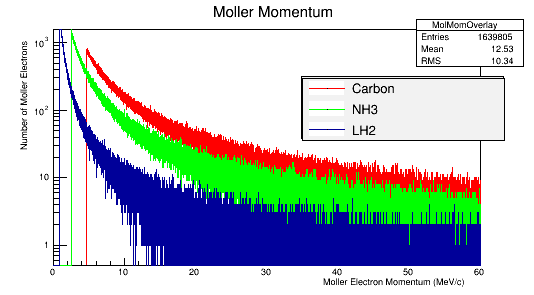
The Moller Momentum plot for higher momenta run to increase the number of values
LH2 Vs. NH3
Figure out the offset
Rerunning the GEANT simulation for a target of solo atoms of Carbon 12, with 410 incident 11GeV electrons
Density of target material:
C=2.26 g/cm3
NH3=.86g/cm3
LH2=.07g/cm3
Altering the density of LH2 to be .86g/cm3 we find
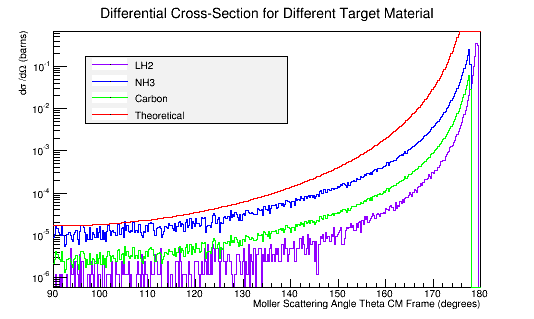
Comparing this to the theoretical differential cross section:
We find that the differential cross section scale is
Converting the number of electrons to barns,
where ρtarget is the density of the target material, ltarget is the length of the target, and iscattered is the number of incident particles scattered.
For LH2:
For Carbon:
For Ammonia:
Combing plots in Root:
new TBrowser();
TH1F *LH2=new TH1F("LH2","LH2",360,90,180);
LH2->Add(MollerThetaCM,1.19e-8);
LH2->Draw();
TH1F *C12=new TH1F("C12","C12",360,90,180);
C12->Add(MollerThetaCM,2.21e-8);
C12->Draw();
TH1F *NH3=new TH1F("NH3","NH3",360,90,180);
NH3->Add(MollerThetaCM,8.87e-8);
NH3->Draw();
LH2->Draw("same");
C12->Draw("same");
Theory->Draw("same");
Step 3
Determine impact of Solenoid magnet on Moller events
Papers used
[1]Farrukh Azfar's Derivation of Moller Scattering
A polarized target for the CLAS detector
An investigation of the spin structure of the proton in deep inelastic scattering of polarized muons on polarized protons
QED Radiative Corrections to Low-Energy Moller and Bhabha Scattering
http://arxiv.org/abs/1602.07609