Scattering Cross Section
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles}{cm^2}\right)} =differential\ scattering\ cross\ section[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
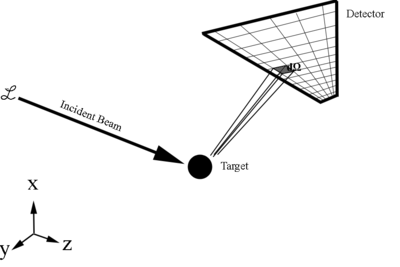[math]\frac{d\sigma}{d\Omega}=\frac{dN}{\mathcal L\, d\Omega}[/math]
[math]where\ dN\ is\ the\ amount\ of\ particles\ per\ unit\ time\ detected,\ also\ called\ the\ event\ rate[/math]
[math]and\ \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi \equiv total\ scattering\ cross\ section[/math]
Transforming Cross Section Between Frames
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames.
[math]\sigma_{CM}=\sigma_{Lab}[/math]
This is a Lorentz invariant.
[math]d\sigma=I_{lab}(\theta_{lab},\ \phi_{lab})\, d\Omega_{lab}=I_{CM}(\theta_{CM},\ \phi_{CM})\, d\Omega_{CM}[/math]
Since the number of particles per second going into the detector is the same for both frames. (Only the z component of the momentum and the Energy are Lorentz transformed)
This is that the number of particles going into the solid-angle element d\Omega and having a moentum between p and p+dp be the same as the number going into the correspoiding solid-angle element d\Omega^* and having a corresponding momentum between p^* and p*+dp*
[math]\left( \begin{matrix} E^* \\ p^*_{x} \\ p^*_{y} \\ p^*_{z}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ p_{1(x)}+p_{2(x)} \\ p_{1(y)}+p_{2(y)} \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)[/math]
