Variables Used in Elastic Scattering

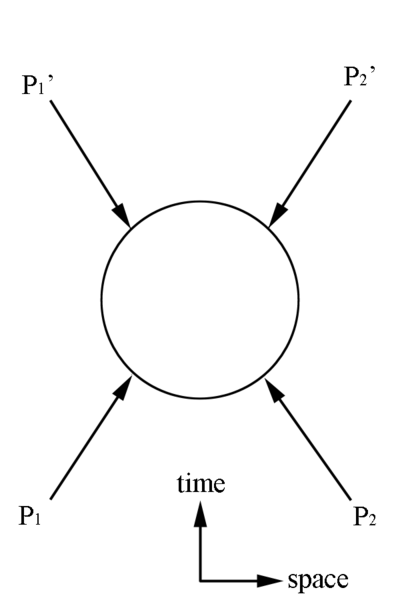
Lorentz Invariant Quantities

As was shown earlier the scalar product of a 4-Momentum vector with itself ,[math]{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s[/math] , and the length of a 4-Momentum vector composed of 4-Momentum vectors, [math]{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s[/math], are invariant quantities.

It was further shown that

[math]{\mathbf P^*}^2={\mathbf P}^2[/math] where [math]{\mathbf P^*}[/math] represents the 4-Momentum Vector in the CM frame and [math]{\mathbf P}[/math] represents the 4-Momentum Vector in the initial Lab frame

which can be expanded to

[math]{\mathbf P^*}^2={\mathbf P}^2={\mathbf P^'}^2[/math] where [math]{\mathbf P^'}[/math] represents the 4-Momentum Vector in the final Lab frame

Mandelstam Representation