Niowave Report 11-30-2015
Overview
10 MeV electron beam
3.48 cm diameter beam pipe
Target optimization
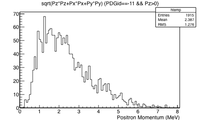
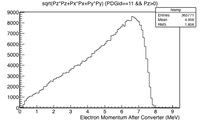
Optimal Thickness
One method to produce positrons relies on the creation of positron-electron pairs from the bremsstrahlung photons that are produced when electrons traverse a dense material. While thicker material encourages the production of these photons, the increased thickness will also cause the produced positrons to annihilate within the material before they can escape. As a result, there is an optimal thickness which will balance the two processes to maximize positron production. A simulation was performed to determine the optimal thickness using a 10 MeV electron beam with a 1cm radius uniform cylindrical spatial distribution impinging a windowless PbBi target. The target thickness was changed to determine the optimal thickness to emmitt positrons from the downstream surface of the PbBi target. The simulation was performed by two separate investigators using separate simualotion packages. The results, shown below, indicate that a PbBi target thicknes of about 2mm will produce about two positrons for every thousand electrons impinging the PbBi target. The postrons leaving the downstream side of the target will have a momentum of approximately 2 MeV whereas the electrons that penetrate the PbBi target will have lost more than 3 MeV.
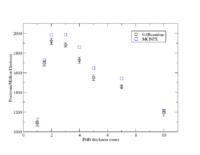
Optimal Solenoidal Field
Beam Pipe heating
The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic field.
The histogram is binned in 100 (10 cm) bin widths. The surface area becomes
To convert From Mev/ e- to kW/cm^2 assuming a current of 1mA (10^-3 C/s) you
 |

|
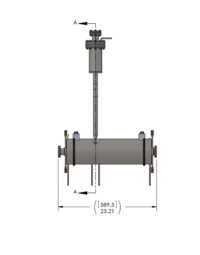
Solenoid Description
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -901 mm.