Difference between revisions of "ISU Coloq 11-3-2014"
| Line 73: | Line 73: | ||
== Definition of Missing Mass== | == Definition of Missing Mass== | ||
| + | ===Inclusive Missing mass W**2=== | ||
| + | Inelastic scattering (Energy is not conserved but absorbed from the momentum transfer) | ||
| + | |||
| + | |||
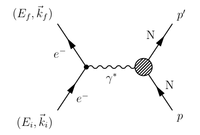
| + | <math>P_e^{\mu} \equiv (E_i,\vec{k}_i)</math> | ||
| + | <math>\left(P_e^{\mu}\right)^{\prime} \equiv (E_f,\vec{k}_f)</math> | ||
| + | <math>P_p^{\mu} \equiv (M_p,0)</math> | ||
| + | <math>\left(P_p^{\mu}\right)^{\prime} \equiv (E_X,\vec{k}_X)</math> | ||
| + | |||
| + | ;4-momentum conservation:<math>P_e^{\mu} + P_p^{\mu} = \left(P_e^{\mu}\right)^{\prime} + \left(P_p^{\mu}\right)^{\prime}</math> | ||
| + | |||
| + | |||
| + | <math>\left(P_p^{\mu}\right)^{\prime} \left(P_{\mu}^p\right)^{\prime} = [P_e^{\mu} + P_p^{\mu} - \left(P_e^{\mu}\right)^{\prime} ][P^e_{\mu} + P^p_{\mu} - \left(P^e_{\mu}\right)^{\prime} ]</math> | ||
| + | |||
| + | <math>E_X^2 - P_X^2 \equiv W^2 = (E_i^2 - k_i^2) + (E_f^2-k_f^2) + M_p^2 + 2M_p(E_i - E_f) -2(E_iE_f-\vec{k_i}\cdot \vec{k_f})</math> | ||
| + | |||
| + | :<math>W^2=M_p^2 + 2M_p(E_i-E_f) -Q^2 \equiv </math>Invariant Missing Mass = mass of the intermediate state that was created. | ||
| + | |||
| + | |||
| + | [[File:CLAS_InelasticSpectrum_2012.png | 200 px]] | ||
== Spin 1/2 and 3/2 final states== | == Spin 1/2 and 3/2 final states== | ||
Revision as of 18:12, 11 October 2014
electron scattering (collisions)
Elastic Collisions: Conserve P and E
Inelastic : Only Conserve P
Definition of Momentum Transfer
Using Ryder 4-momentum tensor convention:
- Conservation of Momentum
- Momentum Transfer
- Momentum Transfer Squared
- A space-like scattering event
Space-like interval: Two events are separated by a space like interval then there isn't enough time passing between them to allow a cause-effect relationship because a photon can't traverse the distance. This means that there is no reference frame that may be used to describe the event as happening at the same spatial location but there is a frame that describes them happening at the same time. If the spacetime interval between the two events is defined as s then for a space-like interval
Time-like interval: Two events are separated by a time like interval if enough time passes between them to allow a cause-effect relationship. This means that there is no reference frame that may be used to describe the event as happening at the same time but there is one that describes them happening at the same spatial location. If the spacetime interval between the two events is defined as s then for a time-like interval
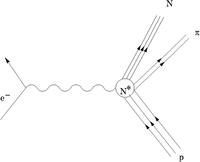
The Delta Resonance
Decay Modes:
- Vector current of the virtual photon exchange
4-Momentum vector definition using Ryder convention
- if you define the speed of light as unity
- Note
- Other conventions used by Perkins
or Kollen
Momentum transfer is defined as
- : conservation of momentum
Definition of Missing Mass
Inclusive Missing mass W**2
Inelastic scattering (Energy is not conserved but absorbed from the momentum transfer)
- 4-momentum conservation
- Invariant Missing Mass = mass of the intermediate state that was created.
Spin 1/2 and 3/2 final states
References
Theory
Phenomenological
NP, B291(1987)793; NP, B346(1990)1;
Z. Phys. C56(1992)493;
Eur. Phys. J. C44 (2005)219;
hep-ph/0205123
arXiV:1310.5285
QCD inspired
NP, B483(1997)291; NP, B484(1997)265;
PRL 85(2000)3591; PRL 89(2002)162301;
JHEP 0211(2002)44; NP, A720(2003)131;
Eur. Phys. J. C30(2003)213; arXiV:09073534;
NP, A761(2005)67; PR, C81(2010)024902
Hybrids
PYTHIA + BUU simulation
PR, C70(2004)054609; NP, A801(2008)68
Experiment
keith's 2012 talk in Italy on EG1-DVCS
Unpolarized
http://link.springer.com/article/10.1007%2FJHEP04%282014%29005
File:AndyMiller 200TalkAtDESY.pdf 2002 talk by CA Miller at DESY
File:Dueren.98.055.pdf 1998 Duren talk
July 30,2014 talk by XingLong Li at Heremes File:XingLongLi TalkOnPACIAEmdoelForSIDIS.pdf from
Xiangs proposal for CLAS12 measurement of SIDIS Xsections see Fig. 1
Semi-inclusive deep inelastic scattering at small transverse momentum
Naomi's SIDIS Hermes talk from 2011 at NNPSS11