Forest UCM Osc 2-DOsc

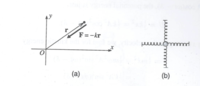
Two Dimensional Oscillators

Isotropic Oscillator

The simplest 2-D oscillator that is composed of identical springs (same spring constant).

[math] \vec F = -k( x \hat i + y \hat j)[/math]

The equations of motion are separable two equations, one for each direction

[math]\ddot x = - \omega^2x \Rightarrow x = A_x \cos(\omega t - \delta_x)[/math]

[math]\ddot y = - \omega^2 y \Rightarrow y = A_y \cos(\omega t - \delta_y)[/math]

you could define a relative phase between the two oscillators as

\delta = \delta_y - \delta_x

it can be substituted into the above equations by shifting the time origin (problem 5.15)

let

[math]t^{\prime} = t + t_0[/math]

then

[math]x = A_x \cos(\omega t^{\prime} - \omega t_0 - \delta_x)[/math]

let

[math]t_0 = \frac{-\delta_x}{\omega}[/math]

[math] x=A_x \cos(\omega t^{\prime} - \omega\frac{-\delta_x}{\omega} - \delta_x)[/math]

[math] =A_x \cos(\omega t^{\prime})[/math]

similarly

[math]y = A_y \cos(\omega t^{\prime} - \omega t_0 - \delta_x)[/math]

[math] =A_y \cos(\omega t^{\prime} - \omega \frac{-\delta_x}{\omega} - \delta_x)[/math]

[math]= A_y \cos(\omega t^{\prime} +\delta_x - \delta_y)[/math]

[math]= A_y \cos(\omega t^{\prime} +\delta)[/math]

Interpretation

[math] =A_x \cos(\omega t^{\prime})[/math]

[math]= A_y \cos(\omega t^{\prime} -\delta)[/math]

There are several modes of motion for the above system of equation

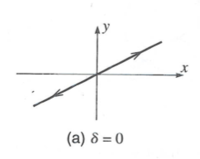
No phase difference

If there is no phase difference then (\delta =0 ) and you have oscillating motion along a line.

90 degree phase difference

If the x and y motions are completely out of phase ( phase difference of 90 degrees or [math]\frac{\pi}{2}[/math])

then the motion is an ellipse (unless their amplitudes are equal in which case the mass moves in a circle).

[math] =A_x \cos(\omega t^{\prime})[/math]

[math]= A_y \cos(\omega t^{\prime} +\frac{\pi}{2})= A_y \sin(\omega t^{\prime})[/math]

If the phase shift is less than 90 then the ellipse is slanted towards the x-axis otherwise it is toward the y-axis.

Anisotropic Oscillator

Forest_UCM_Osc#2-D_Oscillators