|
|
| Line 65: |
Line 65: |
| | | | |
| | :<math>\vec F = -\vec \nabla U</math> | | :<math>\vec F = -\vec \nabla U</math> |
| − | ::<math> = \left ( \hat r \frac{d}{dr} + \hat \theta \frac{1}{r} \frac{d}{d \theta} + \hat \phi \frac{1}{ r \sin \theta } \frac{d}{d\phi} \rigt ) U </math> | + | ::<math> = \left ( \hat r \frac{d}{dr} + \hat \theta \frac{1}{r} \frac{d}{d \theta} + \hat \phi \frac{1}{ r \sin \theta } \frac{d}{d\phi} \right ) U </math> |
| | | | |
| | | | |
Revision as of 18:27, 27 September 2014
A central force is defined as a force depends only on separation distance
- [math]\vec{F} = f(\vec r) \hat r[/math]
ie
Coulomb force and gravitation force.
Spherical Coordinates
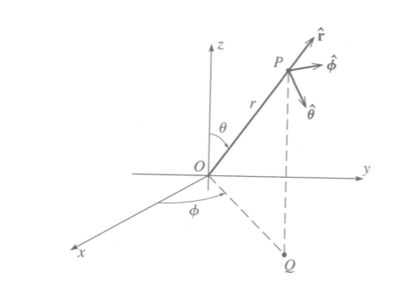
Forest_UCM_NLM_Ch1_CoordSys#Spherical
Gradient in spherical coordinates
The differential change of [math]\vec r[/math] in spherical coordinates occurs in three directions.
In the radial direction
- [math]dr \hat r[/math]
In the polar angle direction
- [math]r d \theta \hat \theta[/math]
In the azimuthal angle direction
- [math]r \sin \phi d \phi \hat \phi[/math]
The differential force of the displacement vector in spherical coordinates is
- [math]d \vec r = dr \hat r + r d \theta \hat \theta + r \sin \phi d \phi \hat \phi[/math]
The derivative may be represented as
- [math]df = f(x+dx) -f(x) = \frac{df}{dx} dx[/math]
in three dimensional cartesian coordinates this may be written in terms of the gradient as
- [math]df = \frac{df}{dx} dx + \frac{df}{dy} dy + \frac{df}{dz} dz =\vec \nabla f \cdot d \vec r[/math]
To determine the gradient in sperical coordinates on just compares the two equations
- [math]\frac{df}{dr} dr + \frac{df}{d \theta} d\theta + \frac{df}{d\phi} d\phi =\vec \nabla f \cdot d \vec r[/math]
- [math]\vec \nabla f \cdot d \vec r = \vec \nabla f \cdot \left ( dr \hat r + r d \theta \hat \theta + r \sin \phi d \phi \hat \phi \right )[/math]
- [math]= \left ( \vec \nabla f \right )_r dr +\left ( \vec \nabla f \right )_{\theta} r d\theta +\left ( \vec \nabla f \right )_{\phi} r \sin \theta d\phi [/math]
comparing terms of the above with
- [math]\left ( \vec \nabla f \right )_r dr =\frac{df}{dr} dr \Rightarrow \left ( \vec \nabla f \right )_r =\frac{df}{dr} [/math]
- [math]\left ( \vec \nabla f \right )_{\theta} r d\theta =\frac{df}{d \theta} d\theta \Rightarrow \left ( \vec \nabla f \right )_{\theta} d\theta =\frac{1}{r} \frac{df}{d \theta} [/math]
- [math] \left ( \vec \nabla f \right )_{\phi} r \sin \theta d\phi =\frac{df}{d\phi} d\phi \Rightarrow \left ( \vec \nabla f \right )_{\phi} d\phi = \frac{1}{ r \sin \theta } \frac{df}{d\phi} [/math]
or
- [math] \vec \nabla = \hat r \frac{d}{dr} + \hat \theta \frac{1}{r} \frac{d}{d \theta} + \hat \phi \frac{1}{ r \sin \theta } \frac{d}{d\phi} [/math]
The Central Force
Spherical symmetry
A central force needs to be spherically symmetric in order to be conservative.
- [math]\vec F = f(\vec r) \hat r[/math]
If the force is conservative then a potential exists such that
- [math]\vec F = -\vec \nabla U[/math]
- [math] = \left ( \hat r \frac{d}{dr} + \hat \theta \frac{1}{r} \frac{d}{d \theta} + \hat \phi \frac{1}{ r \sin \theta } \frac{d}{d\phi} \right ) U [/math]
Forest_UCM_Energy#Central_Forces
