Forest UCM Energy CentralForce

A central force is defined as a force depends only on separation distance

[math]\vec{F} = f(\vec r) \hat r[/math]

ie

Coulomb force and gravitation force.

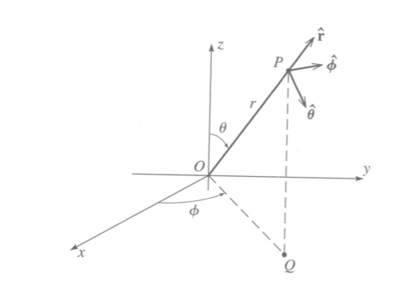
Spherical Coordinates

Forest_UCM_NLM_Ch1_CoordSys#Spherical

Gradient in spherical coordinates

The differential change of [math]\vec r[/math] in spherical coordinates occurs in three directions.

In the radial direction

[math]dr \hat r[/math]

In the polar angle direction

[math]r d \theta \hat \theta[/math]

In the azimuthal angle direction

[math]r \sin \phi d \phi \hat \phi[/math]

The differential force of the displacement vector in spherical coordinates is

[math]d \vec r = dr \hat r + r d \theta \hat \theta + r \sin \phi d \phi \hat \phi[/math]

The derivative may be represented as

[math]df = f(x+dx) -f(x) = \frac{df}{dx} dx[/math]

in three dimensional cartesian coordinates this may be written in terms of the gradient as

[math]df = \frac{df}{dx} dx + \frac{df}{dy} dy + \frac{df}{dz} dz =\vec \nabla f \cdot d \vec r[/math]

To determine the gradient in sperical coordinates on just compares the two equations

[math]\frac{df}{dr} dr + \frac{df}{d \theta} d\theta + \frac{df}{d\phi} d\phi =\vec \nabla f \cdot d \vec r[/math]

[math]\vec \nabla f \cdot d \vec r = \vec \nabla f \cdot \left ( dr \hat r + r d \theta \hat \theta + r \sin \phi d \phi \hat \phi \right )[/math]

[math]= \left ( \vec \nabla f \right )_r dr +\left ( \vec \nabla f \right )_{\theta} r d\theta +\left ( \vec \nabla f \right )_{\phi} r \sin \theta d\phi [/math]

comparing terms of the above with

[math]\left ( \vec \nabla f \right )_r dr =\frac{df}{dr} dr \Rightarrow \left ( \vec \nabla f \right )_r =\frac{df}{dr} [/math]

[math]\left ( \vec \nabla f \right )_{\theta} r d\theta =\frac{df}{d \theta} d\theta \Rightarrow \left ( \vec \nabla f \right )_{\theta} d\theta =\frac{1}{r} \frac{df}{d \theta} [/math]

[math] \left ( \vec \nabla f \right )_{\phi} r \sin \theta d\phi =\frac{df}{d\phi} d\phi \Rightarrow \left ( \vec \nabla f \right )_{\phi} d\phi = \frac{1}{ r \sin \theta } \frac{df}{d\phi} [/math]

or

[math] \vec \nabla = \hat r \frac{d}{dr} + \hat \theta \frac{1}{r} \frac{d}{d \theta} + \hat \phi \frac{1}{ r \sin \theta } \frac{d}{d\phi} [/math]

The Central Force

Forest_UCM_Energy#Central_Forces