Forest UCM Energy CentralForce

A central force is defined as a force depends only on separation distance

[math]\vec{F} = f(\vec r) \hat r[/math]

ie

Coulomb force and gravitation force.

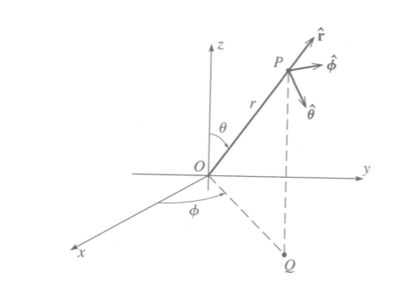
Spherical Coordinates

Forest_UCM_NLM_Ch1_CoordSys#Spherical

The differential change of [math]\vec r[/math] in spherical coordinates occurs in three directions.

In the radial direction

[math]dr \hat r[/math]

In the polar angle direction

[math]r d \theta \hat \theta[/math]

In the aximuthal angle direction

[math]r \sin \phi d \phi \hat \phi[/math]

The differential force of the displacement vector in spherical coordinates is

[math]d \vec r = r dr \hat r + r d \theta \hat \theta + r \sin \phi d \phi \hat \phi[/math]

The derivative may be represented as

[math]df = f(x+dx) -f(x) = \frac{df}{dx} dx[/math]

in three dimensions this may be written in term of the gradient as

[math]df = \vec \nabla f \cdot d \vec r[/math]

[math] = \frac{df}{dr} dr +\frac{df}{d \theta} d \theta +\frac{df}{d \phi} d \phi + [/math]

Gradient in spherical coordinates

Forest_UCM_Energy#Central_Forces