Forest UCM NLM AtwoodMachine

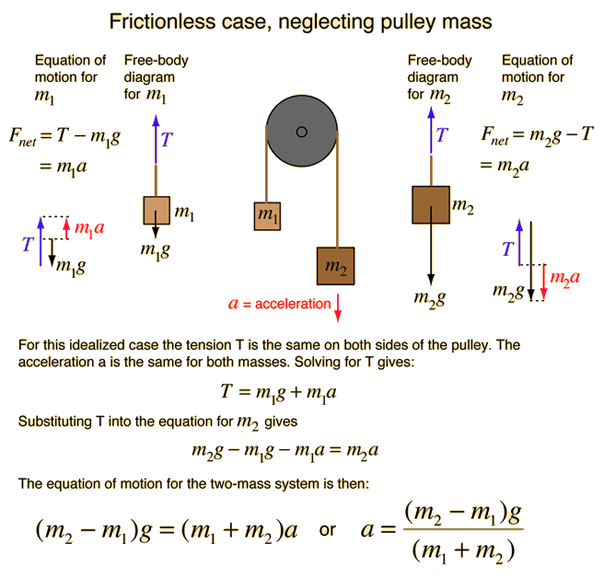
Simple Atwood's machine

[math]\Rightarrow T = \frac{2m_1m_2}{m_1+m_2} g[/math]

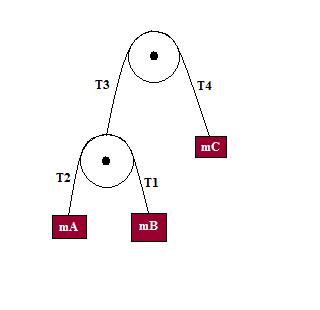
Double Atwood's machine

The problem

Determine the acceleration of each mass in the above picture.

Step 1: Identify the system

Each block is a separate system with two external forces; a gravitational force and the rope tension.

Step 2: Choose a suitable coordinate system

A coordinate system with one axis that defines the posive direction as up is one possible orientation.

Step 3: Draw the Free Body Diagram

200 px

Step 4: Define the Force vectors using the above coordinate system

since the system is one dimensional I will omit the vector notation

[math]T_1=[/math] Tension in the rope attached to mass [math]m_1[/math]

[math]T_2=[/math] Tension in the rope attached to mass [math]m_2 = T_1[/math]

[math]T_3=[/math] Tension in the rope attached to mass [math]m_3[/math]

[math]F_g[/math] = force of gravity on each mass [math]= m_1 g[/math] or [math]m_2 g[/math] or [math]m_3 g[/math]

Step 5: Use Newton's second law

for mass 1

[math]T_1 - m_1 g = m_1 a_1[/math]

for mass 2

[math]T_2 - m_2 g = m_2 a_2[/math]

for mass 3

[math]T_3 - m_3 g = m_3 a_3[/math]

If we know the mass of all the objects in the system then we are left with three unkown Tensions and three unknown acceleratios. In total we currently have 6 unkowns and 3 equations.

Using Newton's third law we know that [math]T_1 = T_2[/math] reducing the unkowns to 5.

We need 2 more equations!

External Forces on Lower pulley

Consider the external forces acting on the MASSLESS lower pulley

[math]T_3-T1-T2 =T_3-T1-(T1) =(0)a[/math]

[math]T_3=2T_1[/math]

Now we have 4 unkwons and 3 equations

relative acceleration

let

[math]a_r =[/math] acceleration of [math]m_1[/math] with respect to the lower pulley

assuming that [math]a_1[/math] is moving upwards with respect to the earth

[math]a_1 = a_r - a_3[/math] : [math]a_3 =[/math] acceleration of lower pully as well as [math]m_3[/math]

similarly

[math]a_2=-a_r-a_3[/math] : if [math]m_1[/math] is accelerating upwards then [math]m_2[/math] is accelerating downwards

3 equations and 3 unknowns

[math]T_1 - m_1 g = m_1 \left ( a_r - a_3 \right )[/math]

[math]T_1 - m_2 g = m_2 \left ( -a_r - a_3 \right )[/math]

[math]\left ( 2 T_1 \right ) - m_3 g = m_3 a_3[/math]

Solutions

solving the above system of equations leads to the solutions

[math]a_1 = \frac{3m_2m_3 -m_1m_3 -4m_1m_2}{m_1m_3 + m_2 m_3 + 4 m_1 m_2}g[/math]

[math]a_2 = \frac{3m_1m_3 -m_2m_3 -4m_1m_2}{m_1m_3 + m_2 m_3 + 4 m_1 m_2}g[/math]

[math]a_3 = \frac{4m_1m_2 -m_2m_3 -m_1m_3}{m_1m_3 + m_2 m_3 + 4 m_1 m_2}g[/math]

Matrix method solution ([math]T_1, a_r, a_3[/math] are the unkowns)

[math]\left( \begin{array}{ccc} 1 & -m_1 & m_1 \\ 1 & m_2 & m_2 \\ 2 & 0 & -m_3 \end{array} \right)\left( \begin{array}{ccc} T_1 \\ a_r \\ a_3 \end{array} \right) = \left( \begin{array}{ccc} m_1 g \\ m_2 g \\ m_3 g\end{array} \right) [/math]

Cramer's Rule:

[math]a_3 = \frac{\left( \begin{array}{ccc} 1 & -m_1 & m_1 \\ 1 & m_2 & m_2 \\ 2 & 0 & -m_3 \end{array} \right)}{\left( \begin{array}{ccc} 1 & -m_1 & m_1 \\ 1 & m_2 & m_2 \\ 2 & 0 & -m_3 \end{array} \right)}[/math]

Forest_UCM_NLM#Atwoods_Machine