Forest UCM NLM GalileanTans

File:TF UCM GalileanTans RefFrame.xfig.txt

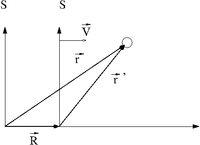
Assume that [math]S^{\prime}[/math] is a coordinate system moving at a CONSTANT speed [math]v[/math] with respect to a fixed coordinate system [math]S[/math].

Let [math]\vec{r}[/math] and [math]\vec{r}^{\prime}[/math] describe the position an object in motion using two different coordinate systems [math]S[/math] and [math]S^{\prime}[/math] respectively.

[math]\vec{R}[/math] represents a vector that locates the origin of the moving reference frame ([math]S^{\prime}[/math]) with respect to the origin of reference from [math]S[/math].

Using the definition of vector addition

[math]\vec{r} = \vec{R} + \vec{r}^{\prime}[/math]

Similarly

[math]\vec{v} = \frac{d \vec{r}}{dt} = \frac{d \vec{R}}{dt} + \frac{d \vec{r}^{\prime}}{dt} [/math]

and

[math]\vec{a} = \frac{d^2 \vec{r}}{dt^2} = \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} [/math]

Newton's law of motion may be written as

[math]\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )[/math]

If

[math]\frac{d^2 \vec{R}}{dt^2}=0[/math] [math]S^{\prime}[/math] is moving at a constant velocity [math]\vec{V}[/math]

Then

[math]\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )[/math]

Newton's law hold in coordinate system which move at a constant velocity (an inertial reference frame). Accelerating reference frames are know as non-inertial reference frames and will be discussed later. (a coordinate system fixed to the Earth is a non-inertial reference frame since the Earth is rotating about its axis and moving in orbit about the Sun)

Galiean Transformation to CM frame

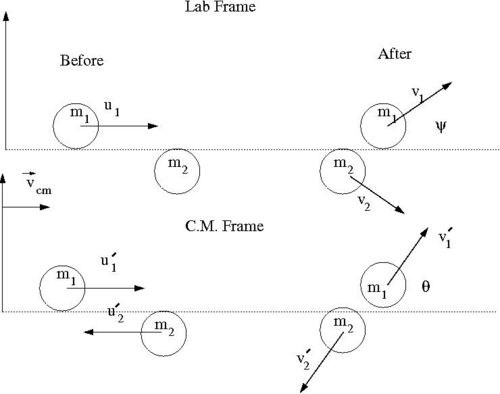
Consider the elastic scattering of two hard spheres from a fixed reference frame (Lab Frame) and an inertial frame moving at a speed [math]\vec{v}_{cm}[/math] such that the momentum of the two spheres are equal in magnitude but opposite in direction.

A feature of elastic collisions described in the center of momentum (mass) frame is that the magnitude of each particles momentum remains the same before and after a collision, only their directions change.

Variable definitions

[math]m_1[/math]= mass of incoming ball

[math]m_2[/math]= mass of target ball

[math]u_1[/math]= iniital velocity of incoming ball in Lab Frame

[math]v_1[/math]= final velocity of [math]m_1[/math] in Lab Frame

[math]\psi[/math]= scattering angle of [math]m_1[/math] in Lab frame after collision

[math]u_1^{\prime}[/math]= iniital velocity of [math]m_1[/math] in C.M. Frame

[math]v_1^{\prime}[/math]= final velocity of [math]m_1[/math] in C.M. Frame

[math]u_2^{\prime}[/math]= iniital velocity of [math]m_2[/math] in C.M. Frame

[math]v_2^{\prime}[/math]= final velocity of [math]m_2[/math] in C.M. Frame

[math]\theta[/math]= scattering angle of [math]m_1[/math] in C.M. frame after collision

In terms of our reference frames

vector definitions

[math]\vec{r}_1[/math] = a position vector pointing to the location of [math]m_1[/math] in the fixed reference frame [math]S[/math]

[math]\vec{r}_2[/math] = a position vector pointing to the location of [math]m_2[/math] in the fixed reference frame [math]S[/math]

[math]\vec{r}_1^{\prime}[/math] = a position vector pointing to the location of [math]m_1[/math] in the fixed reference frame [math]S^{\prime}[/math]

[math]\vec{r}_2^{\prime}[/math] = a position vector pointing to the location of [math]m_2[/math] in the fixed reference frame [math]S^{\prime}[/math]

[math]\vec{R}[/math] = a position vector pointing from the fixed reference frame origin to the moving frame origin

Find the velocity of the center of momentum (mass) frame

By definition the velocity of the center of momentum is

\vec{u}_1 = \vec{v}_{cm} + \vec{u}_1^{\prime}

Forest_UCM_NLM#Galilean_Transformations