Forest UCM NLM GalileanTans

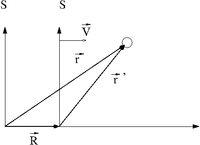
Assume that [math]S^{\prime}[/math] is a coordinate system moving at a CONSTANT speed [math]v[/math] with respect to a fixed coordinate system [math]S[/math].

Let [math]\vec{r}[/math] and [math]\vec{r}^{\prime}[/math] describe the position an object in motion using two different coordinate systems [math]S[/math] and [math]S^{\prime}[/math] respectively.

[math]\vec{R}[/math] represents a vector that locates the origin of the moving reference frame ([math]S^{\prime}[/math]) with respect to the origin of reference from [math]S[/math].

Using the definition of vector addition

[math]\vec{r} = \vec{R} + \vec{r}^{\prime}[/math]

Similarly

[math]\vec{v} = \frac{d \vec{r}}{dt} = \frac{d \vec{R}}{dt} + \frac{d \vec{r}^{\prime}}{dt} [/math]

and

[math]\vec{a} = \frac{d^2 \vec{r}}{dt^2} = \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} [/math]

Newton's law of motion may be written as

[math]\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )[/math]

If

[math]\frac{d^2 \vec{R}}{dt^2}=0[/math] [math]S^{\prime}[/math] is moving at a constant velocity [math]\vec{V}[/math]

Then

[math]\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )[/math]

Newton's law hold in coordinate system which move at a constant velocity (an inertial reference frame). Accelerating reference frames are know as non-inertial reference frames and will be discussed later. (a coordinate system fixed to the earth is a non-inertial reference frame)

Forest_UCM_NLM#Galilean_Transformations