Difference between revisions of "Forest UCM NLM GalileanTans"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
[[File:TF_UCM_GalileanTans_RefFrame.png | 200 px]] | [[File:TF_UCM_GalileanTans_RefFrame.png | 200 px]] | ||
| − | Assume that <math>S^{\prime}</math> is a coordinate system moving at a CONSTANT speed <math>v</math>. | + | Assume that <math>S^{\prime}</math> is a coordinate system moving at a CONSTANT speed <math>v</math> with respect to a fixed coordinate system <math>S</math>. |
| Line 21: | Line 21: | ||
:<math>\vec{a} = \frac{d^2 \vec{r}}{dt^2} = \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} </math> | :<math>\vec{a} = \frac{d^2 \vec{r}}{dt^2} = \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} </math> | ||
| + | |||
| + | Newton's law of motion may be written as | ||
| + | |||
| + | :\vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} \right ) | ||
[[Forest_UCM_NLM#Galilean_Transformations]] | [[Forest_UCM_NLM#Galilean_Transformations]] | ||
Revision as of 12:34, 20 August 2014
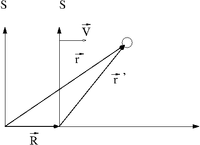
Assume that is a coordinate system moving at a CONSTANT speed with respect to a fixed coordinate system .
Let and describe the position an object in motion using two different coordinate systems and respectively.
represents a vector that locates the origin of the moving reference frame () with respect to the origin of reference from .
Using the definition of vector addition
Similarly
and
Newton's law of motion may be written as
- \vec{F} = m\vec{a} = m \left ( \frac{d^2 \vec{R}}{dt^2} + \frac{d^2 \vec{r}^{\prime}}{dt^2} \right )