Difference between revisions of "Forest UCM NLM Ch1 CoordSys"
(Created page with "Forest_UCM_NLM#Space") |
|||
| Line 1: | Line 1: | ||
| + | Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space. | ||
| + | |||
| + | ===Cartesian=== | ||
| + | |||
| + | [[File:TF_UCM_CartCoordSys.png| 200 px]] | ||
| + | |||
| + | |||
| + | Vector Notation convention: | ||
| + | |||
| + | Position: | ||
| + | |||
| + | :<math>\vec{r} = x \hat{i} + y \hat{j} + z \hat{k} = (x,y,z) = \sum_1^3 r_i \hat{e}_i</math> | ||
| + | |||
| + | Velocity: | ||
| + | |||
| + | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + x\frac{d \hat{i}}{dt} + \cdots</math> | ||
| + | |||
| + | |||
| + | cartesian unit vectors do not change with time (unit vectors for other coordinate system types do) | ||
| + | |||
| + | |||
| + | :<math>\frac{d \hat{i}}{dt} =0 =\frac{d \hat{j}}{dt} =\frac{d \hat{k}}{dt}</math> | ||
| + | |||
| + | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{j} + \frac{d z}{dt}\hat{k} </math> | ||
| + | |||
| + | |||
| + | Similarly Acceleration is given by | ||
| + | |||
| + | |||
| + | :<math>\vec{a}</math> = <math>\frac{d \vec{v}}{dt}</math> = <math>\frac{d^2 x}{dt^2}\hat{i} + \frac{d^2 y}{dt^2}\hat{j} + \frac{d^2 z}{dt^2}\hat{k} </math> | ||
| + | |||
| + | ===Polar=== | ||
| + | [[File:TF_UCM_PolarCoordSys.png| 200 px]] | ||
| + | Vector Notation convention: | ||
| + | |||
| + | Position: | ||
| + | |||
| + | Because <math>\hat{r}</math> points in a unique direction given by <math>\hat{r} = \frac{\vec{r}}{|r|}</math> we can write the position vector as | ||
| + | |||
| + | :<math>\vec{r} = r \hat{r}</math> | ||
| + | |||
| + | :<math>\vec{r} \ne r \hat{r} +\phi \hat{\phi} </math>: <math>\phi</math> does not have the units of length | ||
| + | |||
| + | |||
| + | The unit vectors (<math>\hat{r}</math> and <math>\hat{\phi}</math> ) are changing in time. You could express the position vector in terms of the cartesian unit vectors in order to avoid this | ||
| + | |||
| + | :<math>\vec{r} = r \cos(\phi) \hat{i} + r \sin(\phi)\hat{j}</math> | ||
| + | |||
| + | The dependence of position with <math>\phi</math> can be seen if you look at how the position changes with time. | ||
| + | |||
| + | ====Velocity in Polar Coordinates ==== | ||
| + | |||
| + | Consider the motion of a particle in a circle. At time <math>t_1</math> the particle is at <math>\vec{r}(t_1)</math> and at time <math>t_2</math> the particle is at <math>\vec{r}(t_2)</math> | ||
| + | |||
| + | |||
| + | [[File:TF_UCM_PolarVectDiff.png| 200 px]] | ||
| + | |||
| + | |||
| + | |||
| + | If we take the limit <math>t_2 \rightarrow t_1</math> ( or <math>\Delta t \rightarrow 0</math>) then we can write the velocity of this particle traveling in a circle as | ||
| + | |||
| + | :<math>\hat{r} (t_2)-\hat{r}(t_1) \equiv \Delta \hat{r} = \Delta \phi \hat{\phi}</math> | ||
| + | |||
| + | ::or | ||
| + | |||
| + | :<math>\frac{ d \hat{r}}{dt} = \frac{d \phi}{dt} \hat{\phi}</math> | ||
| + | |||
| + | Thus for circular motion at a constraint radius we get the familiar expression | ||
| + | |||
| + | :<math>\vec{v} = \lim_{\Delta t \rightarrow 0} \frac{\vec{r}(t_2)-\vec{r}(t_1)}{\Delta t}= \lim_{\Delta t \rightarrow 0} \frac{r\left( \hat{r}(t_2) - \hat{r}(t_1)\right)}{\Delta t} = r \frac{\Delta \phi}{\Delta t} \hat{\phi} = r \omega \hat{\phi}</math> | ||
| + | |||
| + | :<math>\vec{v} = r \frac{d \phi}{dt} \hat{\phi}</math> | ||
| + | |||
| + | |||
| + | |||
| + | If the particle is not constrained to circular motion ( i.e.: <math>r</math> can change with time) then the velocity vector in polar coordinates is | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | :<math>\vec{v}</math> = <math>\frac{d r}{dt}\hat{r} + r\frac{d \phi}{dt} \hat{\phi}</math> | ||
| + | |||
| + | :: or in more compact form | ||
| + | |||
| + | :<math>\vec{v}=\vec{\dot{r}} = \dot{r} \hat{r} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}</math> | ||
| + | |||
| + | |||
| + | |||
| + | :linear velocity <math>\equiv v_r </math> Angular velocity <math>\equiv v_{\phi} </math> | ||
| + | |||
| + | ====Acceleration in Polar Coordinates ==== | ||
| + | |||
| + | Taking the derivative of velocity with time gives the acceleration | ||
| + | |||
| + | |||
| + | :<math>\vec{a} = \frac{d \vec{v}}{dt} =\vec{\ddot{r}} </math> | ||
| + | ::<math>= \frac{ d \left (\dot{r} \hat{r} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}\right)}{dt}</math> | ||
| + | ::<math>= \left ( \frac{ d \dot{r}}{dt} \hat{r} + \dot{r} \frac{ d\hat{r}}{dt} \right) + \left ( \frac{d r}{dt} \dot{\phi} \hat{\phi} +r \frac{d \dot{\phi}}{dt} \hat{\phi} +r \dot{\phi} \frac{d \hat{\phi}}{dt} \right )</math> | ||
| + | ::<math>= \left ( \ddot{r} \hat{r} + \dot{r} \dot{\phi}\hat{\phi} \right) + \left ( \dot{r} \dot{\phi} \hat{\phi} +r \ddot{\phi} \hat{\phi} +r \dot{\phi} \frac{d \hat{\phi}}{dt} \right )</math> | ||
| + | |||
| + | |||
| + | We need to find the derivative of the unit vector <math>\hat{\phi}</math> with time. | ||
| + | |||
| + | Consider the position change below in terms of only the unit vector <math>\hat{\phi}</math> | ||
| + | |||
| + | |||
| + | [[File:TF_UCM_PolarPhiUnitVectDiff.png| 400 px]] | ||
| + | |||
| + | |||
| + | Using the same arguments used to calculate the rate of change in <math>\hat{r}</math>: | ||
| + | |||
| + | If we take the limit <math>t_2 \rightarrow t_1</math> ( or <math>\Delta t \rightarrow 0</math>) then we can write the velocity of this particle traveling in a circle as | ||
| + | |||
| + | :<math>\hat{\phi} (t_2)-\hat{\phi}(t_1) \equiv \Delta \hat{\phi} = \Delta \phi (- \hat{r})</math> | ||
| + | |||
| + | ::or | ||
| + | |||
| + | :<math>\frac{ d \hat{\phi}}{dt} = -\frac{d \phi}{dt} \hat{r}</math> | ||
| + | |||
| + | :<math>\frac{d \hat{\phi}}{dt}= -\dot{\phi} \hat{r}</math> | ||
| + | |||
| + | Substuting the above into our calculation for acceleration: | ||
| + | |||
| + | |||
| + | :<math>\vec{a} = \left ( \ddot{r} \hat{r} + \dot{r} \dot{\phi}\hat{\phi} \right) + \left ( \dot{r} \dot{\phi} \hat{\phi} +r \ddot{\phi} \hat{\phi} +r \dot{\phi} \frac{d \hat{\phi}}{dt} \right )</math> | ||
| + | ::<math>= \left ( \ddot{r} \hat{r} + \dot{r} \dot{\phi}\hat{\phi} \right) + \left ( \dot{r} \dot{\phi} \hat{\phi} +r \ddot{\phi} \hat{\phi} +r \dot{\phi} \left( -\dot{\phi} \hat{r}\right) \right )</math> | ||
| + | ::<math>= \left ( \ddot{r} -r\dot{\phi}^2 \right) \hat{r} + \left ( 2\dot{r} \dot{\phi} +r \ddot{\phi} \right ) \hat{\phi} </math> | ||
| + | |||
| + | For the case of circular motion at constant <math> r (\dot{r} = 0)</math> | ||
| + | |||
| + | :<math>\vec{a} = -r\dot{\phi}^2 \hat{r} + r \ddot{\phi} \hat{\phi} </math> | ||
| + | |||
| + | radial (centripetal, center seeking) acceleration <math>\equiv -r\dot{\phi}^2 \hat{r} = -r \omega^2 \hat{r}</math> | ||
| + | |||
| + | |||
| + | angular (tangential) acceleration <math>\equiv r \ddot{\phi} \hat{\phi} = r \alpha \hat{\phi}</math> | ||
| + | |||
| + | If <math>\dot{r} \ne 0</math> | ||
| + | |||
| + | Then there are two additional terms | ||
| + | |||
| + | :<math>\ddot{r} \hat {r}</math> = radial acceleration | ||
| + | |||
| + | :<math>2\dot{r} \dot{\phi} \hat {\phi}</math> = Coriolis acceleration (to be described later) | ||
| + | |||
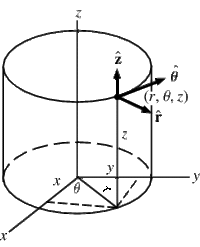
| + | ===Cylindrical=== | ||
| + | |||
| + | [[File:TF_UCM_CylCoordSys.png| 200 px]] | ||
| + | |||
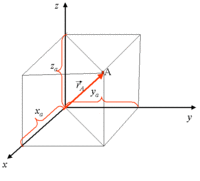
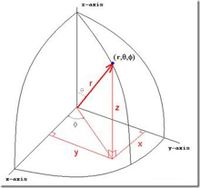
| + | ===Spherical=== | ||
| + | [[File:TF_UCM_SphericalCoordSys.png| 200 px]] | ||
| + | |||
| + | |||
[[Forest_UCM_NLM#Space]] | [[Forest_UCM_NLM#Space]] | ||
Revision as of 20:20, 19 June 2014
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
Cartesian
Vector Notation convention:
Position:
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =
Similarly Acceleration is given by
- = =
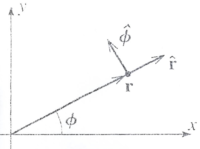
Polar
Position:
Because points in a unique direction given by we can write the position vector as
- : does not have the units of length
The unit vectors ( and ) are changing in time. You could express the position vector in terms of the cartesian unit vectors in order to avoid this
The dependence of position with can be seen if you look at how the position changes with time.
Velocity in Polar Coordinates
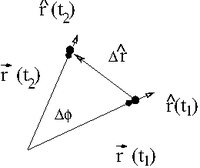
Consider the motion of a particle in a circle. At time the particle is at and at time the particle is at
If we take the limit ( or ) then we can write the velocity of this particle traveling in a circle as
- or
Thus for circular motion at a constraint radius we get the familiar expression
If the particle is not constrained to circular motion ( i.e.: can change with time) then the velocity vector in polar coordinates is
- =
- or in more compact form
- linear velocity Angular velocity
Acceleration in Polar Coordinates
Taking the derivative of velocity with time gives the acceleration
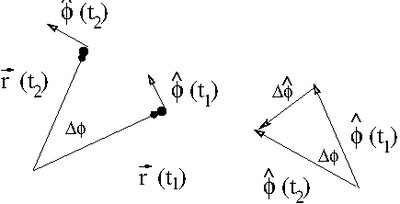
We need to find the derivative of the unit vector with time.
Consider the position change below in terms of only the unit vector
Using the same arguments used to calculate the rate of change in :
If we take the limit ( or ) then we can write the velocity of this particle traveling in a circle as
- or
Substuting the above into our calculation for acceleration:
For the case of circular motion at constant
radial (centripetal, center seeking) acceleration
angular (tangential) acceleration
If
Then there are two additional terms
- = radial acceleration
- = Coriolis acceleration (to be described later)