Forest UCM NLM

Newton's Laws of Motion

Limits of Classical Mechanic

Classical Mechanics is the formulations of physics developed by Newton (1642-1727), Lagrange(1736-1813), and Hamilton(1805-1865).

It may be used to describe the motion of objects which are not moving at high speeds (0.1$c$) nor are microscopically small ( $10^{-9} m$).

The laws are formulated in terms of space, time, mass, and force:

Space and Time

Space

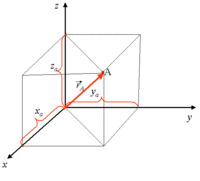
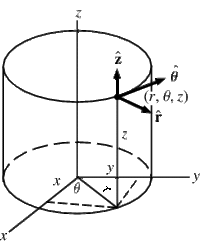
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.

Cartesian

Vector Notation convention:

Position:

$\vec{r} = x \hat{i} + y \hat{j} + z \hat{k} = (x,y,z) = \sum_1^3 r_i \hat{e}_i$

Velocity:

$\vec{v}$ = $\frac{d \vec{r}}{dt}$ = $\frac{d x}{dt}\hat{i} + x\frac{d \hat{i}}{dt} + \cdots$

cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)

$\frac{d \hat{i}}{dt} =0 =\frac{d \hat{j}}{dt} =\frac{d \hat{k}}{dt}$

$\vec{v}$ = $\frac{d \vec{r}}{dt}$ = $\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i}$

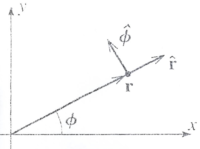
Polar

Vector Notation convention:

Position:

Because $\hat{r}$ points in a unique direction given by $\hat{r} = \frac{\vec{r}}{|r|}$ we can write the position vector as

$\vec{r} = r \hat{r}$

$\vec{r} \ne r \hat{r} +\phi \hat{\phi}$: $\phi$ does not have the units of length

The unit vectors ($\hat{r}$ and $\hat{\phi}$ ) are changing in time. You could express the position vector in terms of the cartesian unit vectors in order to avoid this

$\vec{r} = r \cos(\phi) \hat{i} + r \sin(\phi)\hat{j}$

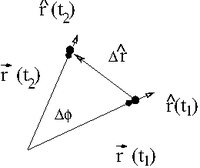
The dependence of position with $\phi$ can be seen if you look at how the position changes with time.

Consider the motion of a particle in a circle. At time $t_1$ the particle is at $\vec{r}(t_1)$ and at time $t_2$ the particle is at $\vec{r}(t_2)$

If we take the limit $t_2 \rightarrow t_1$ ( or $\Delta t \rightarrow 0$) then we can write the velocity of this particle traveling in a circle as

$\hat{r} (t_2)-\hat{r}(t_1) \equiv \Delta \hat{r} = \Delta \phi \hat{\phi}$

or

$\frac{ d \hat{r}}{t} = \frac{d \phi}{dt} \hat{\phi}$

Thus for circular motion at a constraint radius we get the familiar expression

$\vec{v} = \lim_{\Delta t \rightarrow 0} \frac{\vec{r}(t_2)-\vec{r}(t_1)}{\Delta t}= \lim_{\Delta t \rightarrow 0} \frac{r\left( \hat{r}(t_2) - \hat{r}(t_1)\right)}{\Delta t} = r \frac{\Delta \phi}{\Delta t} \hat{\phi} = r \omega \hat{\phi}$

$\vec{v} = r \frac{d \phi}{dt} \hat{\phi}$

If the particle is not constrained to circular motion ( i.e.: $r$ can change with time) then the velocity vector in polar coordinates is

Velocity:

$\vec{v}$ = $\frac{d \vec{r}}{dt}\hat{r} + r\frac{d \phi}{dt} \hat{\phi}$

or in more compact form

$\vec{v}=\vec{\dot{r}} = \dot{r} \hat{r} + r \dot{\phi} \hat{\phi}$

cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)

$\frac{d \hat{i}}{dt} =0 =\frac{d \hat{j}}{dt} =\frac{d \hat{k}}{dt}$

$\vec{v}$ = $\frac{d \vec{r}}{dt}$ = $\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i}$

Spherical

Cylindrical

Vectors

Vector ( Cross ) product

Forest_Ugrad_ClassicalMechanics