Difference between revisions of "Sadiq Thesis Latex"
| Line 999: | Line 999: | ||
\chapter{Conclusions and Suggestions} | \chapter{Conclusions and Suggestions} | ||
| − | The HRRL cavity was moved to current location. New magnetic elements and diagnostic tolls were added to the beamline. The new HRRL beamline was successfully reconfigured to | + | The HRRL cavity was moved to current location. New magnetic elements and diagnostic tolls were added to the beamline. The new HRRL beamline was successfully reconfigured to produce positrons while still can transport electrons to the experimental cell. |
An OTR based diagnostic tool was developed and used to measure the beam emittance of the HRRL. The electron beam profile was not described well using a single Gaussian distribution but rather by a super Gaussian or Lorentzian distribution. The projected emittance of the HRRL was measured to be less than 0.4~$\mu$m as measured by the OTR based tool described above when accelerating electrons to an energy of 15~MeV. | An OTR based diagnostic tool was developed and used to measure the beam emittance of the HRRL. The electron beam profile was not described well using a single Gaussian distribution but rather by a super Gaussian or Lorentzian distribution. The projected emittance of the HRRL was measured to be less than 0.4~$\mu$m as measured by the OTR based tool described above when accelerating electrons to an energy of 15~MeV. | ||
| − | Successfully constructed | + | Successfully constructed a positron detection system using two NaI detectors and the thin tungsten target placed in the 6-way cross. Successfully measured positrons at different energies (1 $-$ 5~MeV) in experiment. The ratio of positrons being detected on NaI detectors to electrons incident on T2 is on the order of $10^{-15}$ and the peak is observed around 3~MeV. |
| + | %In the experiment, quadrapoles were optimized to only transport 2~MeV and due to the limited beam time and it could have diminished transportation efficiency for other energies. %Further experimental study is necessary to investigate the positron beam energy distribution. | ||
Simulation results indicate that the transportation efficiency varies for different energies. Higher energies has better transportation efficiency. While simulation results agree with experiment in that the peak energy distribution is around 3~MeV, it predicts higher positron to electron ratio as shown in the Fig~\ref{fig:e+2e-exp-sim}. %Beam loss | Simulation results indicate that the transportation efficiency varies for different energies. Higher energies has better transportation efficiency. While simulation results agree with experiment in that the peak energy distribution is around 3~MeV, it predicts higher positron to electron ratio as shown in the Fig~\ref{fig:e+2e-exp-sim}. %Beam loss | ||
Revision as of 07:12, 10 September 2013
overlay positron energy distribution at T1 with what is seen at T2 for several values of Q7 Put the e+ simulated results results with experimentally detected results. Flux weighted cross section for positron production. Put the scintilator calibration in the thesis: Mean of ADC9 vs charge on the scope. Separate simulated and experimental systematic errors, then put them together in conclusions.
Text
Anstract
\addcontentsline{toc}{chapter}{Abstract} \chapter*{Abstract}
Positrons were produced using a tungsten target when impinged by an electron beam from the High Repetition Rate Linac (HRRL) at the Beam Lab of the Physics Department at Idaho State University (ISU). % To measure the intensity of positrons at five (1-5~MeV) different energies, two dipoles were used to bend positrons to the second tungsten target where they annihilate and create 511~keV photons. 511~keV photons were measured using two NaI detectors placed horizontally and operated in coincidence. % The positron beam creation and loss are explained with simulation studies using G4beamline. The simulation results are compared with the experiment. Although positron distribution in both simulation and experiment peaked at 3~MeV, the simulation predicted higher counts than the experiment.
Introduction
\chapter{Introduction}
\section{Positron Beam}
Positrons are used in several disciplines of sciences, like chemistry, physics, material science, surface science, biology and nanoscience~\cite{Chemerisov:2009zz}. Different approaches are used to generate positrons. The main challenge is increasing the intensity (or current) of the positron beam. One of the most common methods used to generate a positron beam is using an electron linac. The electron beam produces a positron beam by bremsstrahlung and pair production. One of the advantages of the linac based positron beam is its variable energy and intensity. %Other applications of positron
\subsection{Positron Beam for Positron Annihilation Spectroscopy} Positron annihilation spectroscopy is a non-damaging technique to detect defects in materials. It is based on the fact that positrons tend to annihilate near defects in the material~\cite{Pos-app1}. Different depths of the materials can be probed by using variable energy positron source and a linac based variable energy positron source may be used for this purpose. %Being the anti-matter of electron, it can be used to as high density energy source via annihilation in long term perspective [citation]. %Positrons can be transported to the cancer tumor and the radiation they emit in the annihilation can be used to kill the cancer cell [citation].
%\subsection{Positron Production Using Low Energy Electron Linac} \subsection{Positron Beam for Measuring The Impact of Two Photon Exchange } %Low energy positron beam The nucleon electromagnetic form factors are fundamental quantities that are related to the charge and magnetization distribution in the nucleon. Conventionally, the nucleon form factors are measured using the Rosenbluth Technique (RT)~\cite{Rosenbluth1950}. The form factor scaling ratio, \begin{math}R=\mu _p G_{Ep} / G_{Mp}\end{math}, is measured using this technique is around unity as shown in the Fig.~\ref{rosen-com-RPT}~\cite{PhysRevD.49.5671}. Since the 1990's, a technique using elastic electron-proton polarization transfer to measure this ratio has been developed~\cite{PhysRevD.49.5671, PhysRevC.68.034325, WalkerThesis1989}. In this technique, form factor scaling ratio linearly decreases as the \begin{math}Q^2\end{math} increases, as shown in the Fig.~\ref{rosen-com-RPT}.
\begin{figure} \centering \includegraphics[scale=0.70]{1-Introduction/Figures/Sadiq_thesis_mot_RT_RPT_1.png} \caption{Form factor ratio, obtained by Rosenbluth Technique (hollow square) and results from Recoil Polarization Technique~\cite{PhysRevC.68.034325}.} \label{rosen-com-RPT} \end{figure}
The disagreement could arise from the fact that the Rosenbluth Techqniue assumes that only One Photon Exchange (OPE) occurs during the scattering while the Two Photon Exchange (TPE), which depends weakly on \begin{math}Q^2\end{math}, could also become considerable with increasing \begin{math}Q^2\end{math}~\cite{PhysRevC.68.034325}. The contribution of TPE can be obtained by comparing the ratio of \begin{math}e^+~p\end{math} to \begin{math}e^-~p\end{math} scattering. The interference of OPE and TPE can also be studied in the scattering process \begin{math}e^+e^- \rightarrow p\bar p\end{math}.
\section{Positron Beam Generation from Bremsstrahlung}
When a moving charged particle interacts with the electric field of another charged particle, it can be deflected and lose energy in the form of photons, as shown in the Fig.~\ref{fig:Theo-Brem}. This interaction is known as the bremsstrahlung process. The probability of this interaction increases with the atomic number of the material traversed by the incident charged particle. The Fig.~\ref{fig:Brems_photon_Ene} shows the photon energy distribution produced when the 12~MeV electron energy distribution from the Fig.~\ref{fig:Theo-Brems_ele_Ene} interacts with a 1~mm thick tungsten target. As shown in the Fig.~\ref{fig:Brems_photon_Ene}, the distribution peaks at 0.3~MeV. As the photon energy increases the number of photons produced decreases.
\begin{figure} \centering \includegraphics[scale=0.40]{2-Theory/Figures/bremsstrahlung/brems.eps} \caption{Photon generation from bremsstrahlung processes.} \label{fig:Theo-Brem} \end{figure}
The bremsstrahlung cross section given is by~\cite{brms-cors} \begin{equation} d \sigma = 4 Z^2r_e^2 \alpha \frac{d \nu}{\nu} \left \{ \left (1 + \left( \frac{E}{E_0} \right )^2 \right ) \left [ \frac{\phi_1(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] - \frac{2E}{3E_0} \left [ \frac{\phi_2(\gamma)}{4} - \frac{1}{3} \ln Z -f(Z)\right ] \right \}, \label{eq:Brem-cross} \end{equation} \noindent where $E_0$ is initial total energy of the electron, $E$ is final total energy of the electron, $\nu = \frac{E_0-E}{h}$ is frequency of the emitted photon, and $Z$ is atomic number of the target. $\gamma = \frac{100 m_ec^2 h \nu}{E_0 E Z^{1/3}}$ is charge screening parameter and $f(Z)$ is given by \begin{equation} f(Z) = (Z \alpha)^2 \sum_1^{\infty} \frac{1}{ n [ n^2 + (Z \alpha)^2]}, \end{equation} \noindent where $\alpha = \frac{1}{137}$ is fine-structure constant, $\phi_1$ and $\phi_2$ are screening functions that depend on Z. \begin{figure} \centering \includegraphics[scale=0.70]{2-Theory/Figures/En_photon_dnT1_logY.eps} \caption{Bremsstrahlung photon energy right after a tungsten foil in simulation.} \label{fig:Brems_photon_Ene} \end{figure} \begin{figure} \centering \includegraphics[scale=0.70]{2-Theory/Figures/En_e_upT1.eps} \caption{The electron energy distribution incident on a tungsten foil in simulation.} \label{fig:Theo-Brems_ele_Ene} \end{figure}
There are three competing processes that a photon can undergo when interacting with matter. The Fig.~\ref{fig:Theo-3pro-in-W} are the cross-sections for different types of photon interactions with tungsten as a function of photon energy. At electron volt (eV) energies which is comparable to the electron atomic binding energy, the dominant photon interaction is via the photoelectric effect. As the photon energy increases up to kilo electron volt (keV) range, the Compton scattering process starts to be more dominant. Although the photon is totally absorbed during the photoelectric effect, photons merely lose energy when undergoing the Compton scattering. As the photon energy reaches twice the rest mass energy of the electron, $i.e.$ 2 \begin{math} \times \end{math} 511~keV, the pair production begins to occur. The pair production becomes the dominant interaction process when photon energies are beyond 5~MeV~\cite{Krane}. In this process, a photon interacts with the electric field of the nucleus or the bound electrons and is converted into an electron and positron pair.
\begin{figure} \centering \includegraphics[scale=0.36]{2-Theory/Figures/xcom/Xcom9.eps} \caption{The cross-sections for different types of photon interactions with tungsten as a function of photon energy~\cite{nistxcom}.} \label{fig:Theo-3pro-in-W} \end{figure}
Using natural unit, where \begin{math}c \equiv 1\end{math}, the differential cross-section for pair production can be expressed as \begin{equation} \begin{array}{l} \frac{d \sigma}{d \epsilon_1 d \theta_1 d \theta_2} = 8 \left ( \frac{\pi a}{\sinh (\pi a)} \right )^2 \frac{a^2}{2 \pi} \frac{e^2}{\hbar c} \left ( \frac{\hbar}{m_e c }\right )^2 \frac{\epsilon_1 \epsilon_2}{k^3} \theta_1 \theta_2 \\ \\ \times \left \{ \frac{V^2(x)}{q^4} \left [ k^2 (u^2 + v^2) \xi \eta - 2 \epsilon_1 \epsilon_2 (u^2 \xi^2 + v^2 \eta^2 ) + 2 (\epsilon_1^2 + \epsilon_2^2)uv \xi \eta cos(\phi) \right ] \right . \\ \\ \left . + a^2W^2(x) \xi^2 \eta^2 \left [ k^2(1 - (u^2+v^2)\xi \eta - 2 \epsilon_1 \epsilon_2 (u^2 \xi^2 + v^2 \eta^2) -2 (\epsilon_1^2 + \epsilon_2^2) u v \xi \eta \cos(\phi)\right ]\right \}, \\ \end{array} \end{equation}
\noindent where $k$ is photon energy, $\theta_{1}$ and $\theta_2$ are the scattering angle of $e^+$ and $e^-$ respectively, $ \phi = \phi_1 - \phi_2$ is the angle between the $e^+$ and $e^-$ pair, $\epsilon_1$ and $\epsilon_2$ are the energy of the positron and electron respectively. Other constants are $u = \epsilon_1 \theta_1$, $v=\epsilon_2 \theta_2$, $\xi = \frac{1}{1+u^2}$, $\eta= \frac{1}{1+v^2}$, $q^2 = u^2 + v^2 + 2 u v \cos(\phi)$, $x= 1-q^2 \xi \eta$, $a = \frac{Ze^2}{\hbar c}$, $V(x) = 1 + \frac{a^2}{(1!)^2} + \frac{a^2 (1+a^2) x^2}{(2!)^2} + \frac{a^2 (1+a^2)(2^2+a^2)x^4 x^2}{(3!)^2} + \cdots$, and $W(x) = \frac{1}{a^2} \frac{d V(x)}{d x}$.
In pair production, positron and electron pairs are created back to back in the center of mass frame. In the lab frame, electrons and positrons tend to move in the direction of the photon, as shown in the Fig.~\ref{fig:Theo-pair-pro}. The positron and electron carry away the energy from the photon that is in excess of 1.022~MeV. In the center of mass frame, the kinetic energy is equally shared. Photons with an energy above 1.022~MeV in the bremsstrahlung spectrum of the Fig.\ref{fig:Brems_photon_Ene} have the potential to create electron and positron pairs. The Fig.~\ref{fig:Theo-brem} is the simulation of 10 million 12~MeV mono energy electrons impinging on a tungsten target with 1.016~mm thickness. Turning on the annihilation process resulted in a 511~keV peak on top of the bremsstrahlung spectrum. This 511~keV peak represents photons produced when the created positrons from the pair production annihilate with atomic electrons inside the tungsten target.
\begin{figure} \centering \includegraphics[scale=0.650]{2-Theory/Figures/Pair_Production/Pair_Production.png} \caption{Pair production.} \label{fig:Theo-pair-pro} \end{figure}
\begin{figure} \centering {\scalebox{0.75} [0.7]{\includegraphics{2-Theory/Figures/pair/on/Eng2.eps}}} \\ \caption{Photon spectrum of created by million 12~MeV mono energy electrons impinging on a 1.016~mm thick tungsten target.} \label{fig:Theo-brem} \end{figure}
\section{Emittance Measurement} Emittance is an important parameter in accelerator physics. When the emittance and Twiss parameters are given at the exit of the gun, one will be able to calculate the beam size and the divergence at any given point along the beamline. To study the process of positron creation, one need to know the beam size and divergence on the target. Emittance and Twiss parameters are input parameters for any accelerator simulation tools that can be used to study the experimental processes and to make predictions.
\subsection{Emittance} In accelerator physics, Cartesian coordinate system is used to describe the motion of the accelerated particles. The $z$-axis of Cartesian coordinate system is defined as the natural coordinate that is going along the electron beam line. The $x$-axis and $y$-axis are horizontal and vertical coordinates which constitute the transverse beam profile. For the convenience of representation, one may use $z$ to represent transverse coordinates and express longitudinal profile with natural coordinates $s$ along the beamline. The transverse beam profiles are described as a function of the longitudinal coordinate, $i.e.$ $x(s)$ and $y(s)$. The angle of an accelerated charge regarding the designed orbit can be defined as $z'=\frac{dz}{ds}$.
The phase space $z'$ vs. $z$ of the beam is an ellipse with invariant area (along the beamline). This invariant is called the Courant-Snyder invariant~\cite{Conte}. The transverse emittance $\epsilon$ of the beam is defined to be the area of the ellipse that contains 90\% of the particles. Beam divergence and Twiss parameters are related to the beam size and divergence by \begin{equation} \sigma_{x}(s)=\sqrt{\epsilon _x (s) \beta _x (s)},~ \sigma_{x'}(s)=\sqrt{\epsilon _x (s) \gamma _x (s)}, \label{eq:twiss-emit} \end{equation}
\noindent where $\epsilon_{x}$ is beam horizontal emittance, $\sigma_{x}$ is rms beam size, $\sigma_{x'}$ is rms beam divergence, and $\beta _x $ and $\gamma _x$ are two of the Twiss parameters.
\subsection{Emittance Measurement} The HRRL beam emittance was measured using an Optical Transition Radiation (OTR). Transition radiation was theoretically predicted by Ginzburg and Frank~\cite{Ginzburg-Frank} in 1946 to occur when a charged particle passes the boundary of two medium and emits radiation. %The particle carries certain field when it passes through certain medium with certain motion~\cite{ENM-Jackson}. When it passes into the second medium, it has to reorganize its field characteristics at the boundary, and emit pieces of the field in the form electromagnetic radiation. The fields are emitted in the forward and backward directions~\cite{OTR-Gitter}. The backward radiated photons An OTR based viewer was installed to observe electron beam size at the high electron currents, available using the HRRL at 15~MeV with 200~ns macro pulse width and 37.2~mA peak current. The visible light is produced when a relativistic electron beam crosses the boundary of two mediums with different dielectric constants. Visible radiation is emitted at an angle of 90${^\circ}$ with respect to the incident beam direction when the electron beam intersects the target at a 45${^\circ}$ angle. These backward-emitted photons are observed using a digital camera and can be used to measure the shape and the intensity of the electron beam based on the OTR distribution. Although an emittance measurement can be performed in a several ways~\cite{emit-ways, sole-scan-Kim}, the quadrupole scanning method~\cite{quad-scan} was used to measure the emittance, Twiss parameters, and beam energy in this work.
\subsection{Quadrupole Scanning Method} Fig.~\ref{q-scan-layout} illustrates the beamline components used to measure the emittance for the quadrupole scanning method. A quadrupole is positioned at the exit of the linac to focus or de-focus the beam as observed on the OTR view screen. The 3.1~m distance between the quadrupole and the screen was chosen in order to minimize chromatic effects and to satisfy the thin lens approximation. %The quadrupole and the screen are located far away to minimize chromatic effects and to increase the veracity of the thin lens approximation used to calculate beam optics. \begin{figure} \centering \includegraphics[scale=0.55]{3-Apparatus/MOPPR087f1.eps} \caption{Apparatus used to measure the beam emittance.} \label{q-scan-layout} \end{figure} Assuming the thin lens approximation, $\sqrt{k_1}L << 1$, is satisfied, the transfer matrix of a quadrupole magnet may be expressed as % thin lens approximation (sqrt{k1}*L << 1). In our case sqrt{k1}*L =0.07 \begin{equation} \label{quad-trans-matrix} \mathrm{\mathbf{Q}}=\Bigl(\begin{array}{cc} 1 & 0\\ -k_{1}L & 1 \end{array}\Bigr)=\Bigl(\begin{array}{cc} 1 & 0\\ -\frac{1}{f} & 1 \end{array}\Bigr), \end{equation} where $k_{1}$ is the quadrupole strength, $L$ is the length of quadrupole, and $f$ is the focal length. A matrix representing the drift space between the quadrupole and screen is given by \begin{equation} \label{drift-trans-matrix} \mathbf{\mathbf{S}}=\Bigl(\begin{array}{cc} 1 & l\\ 0 & 1 \end{array}\Bigr), \end{equation} where $l$ is the distance between the scanning quadrupole and the screen. The transfer matrix $\mathbf{M}$ of the scanning region is given by the matrix product $\mathbf{SQ}$. In the horizontal plane, the beam matrix at the screen ($\mathbf{\sigma_{s}}$) is related to the beam matrix of the quadrupole ($\mathbf{\sigma_{q}}$) using the similarity transformation \begin{equation} \mathbf{\mathbf{\sigma_{s}=M\mathrm{\mathbf{\mathbf{\sigma_{q}}}}}M}^{\mathrm{T}}. \end{equation} where the $\mathbf{\sigma_{s}}$ and $\mathbf{\sigma_{q}}$ are defined as~\cite{SYLee} \begin{equation} \mathbf{\mathbf{\sigma_{s,\mathnormal{x}}=}}\Bigl(\begin{array}{cc} \sigma_{\textnormal{s},x}^{2} & \sigma_{\textnormal{s},xx'} \\ \sigma_{\textnormal{s},xx'} & \sigma_{\textnormal{s},x'}^{2} \end{array}\Bigr) ,\; \mathbf{\mathbf{\sigma_{q,\mathnormal{x}}}}=\Bigl(\begin{array}{cc} \sigma_{\textnormal{q},x}^{2} & \sigma_{\textnormal{q},xx'}\\ \sigma_{\textnormal{q},xx'} & \sigma_{\textnormal{q},x'}^{2} \end{array}\Bigr). \end{equation} \noindent %By defining the new parameters~\cite{quad-scan}, $A \equiv \sigma_{11},~B \equiv \frac{\sigma_{12}}{\sigma_{11}},~C \equiv\frac{\epsilon_{x}^{2}}{\sigma_{11}}$ By defining the new parameters~\cite{quad-scan} \begin{equation} A \equiv l^2\sigma_{\textnormal{q},x}^{2},~B \equiv \frac{1}{l} + \frac{\sigma_{\textnormal{q},xx'}}{\sigma_{\textnormal{q},x}^{2}},~\text{and}~C \equiv l^2\frac{\epsilon_{x}^{2}}{\sigma_{\textnormal{q},x}^{2}}. \end{equation} The matrix element $\sigma_{\textnormal{s},x}^{2}$, the square of the rms beam size at the screen, may be expressed as a parabolic function of the product of $k_1$ and $L$ \begin{equation} \sigma_{\textnormal{s},x}^{2}=A(k_{1}L)^{2}-2AB(k_{1}L)+(C+AB^{2}). \label{par_fit} \end{equation}
The emittance measurement was performed by changing the quadrupole current, which changes $k_{1}L$, and measuring the corresponding beam image on the view screen. The measured two-dimensional beam image was projected along the image's abscissa and ordinate axes. A Gaussian fitting function is used on each projection to determine the rms value, $\sigma_{\textnormal{s}}$ in Eq.~(\ref{par_fit}). Measurements of $\sigma_{\textnormal{s}}$ for several quadrupole currents ($k_{1}L$) is then fit using the parabolic function in Eq.~(\ref{par_fit}) to determine the constants $A$, $B$, and $C$. The emittance ($\epsilon$) and the Twiss parameters ($\alpha$ and $\beta$) can be found using Eq.~(\ref{emit-relation}). \begin{equation} \epsilon=\frac{\sqrt{AC}}{l^2},~\beta=\sqrt{\frac{A}{C}},~\alpha=\sqrt{\frac{A}{C}}(B+\frac{1}{l}). \label{emit-relation} \end{equation}
Apparatus
\chapter{Apparatus} \section{HRRL Beamline} A 16~MeV S-band High Repetition Rate Linac (HRRL) located at the Beam Lab of the Department of Physics, Idaho State University is used to generate incident 12~MeV electron beam on a tungsten foil. The energy of the HRRL is tunable between 3 to 16~MeV and its repetition rate variable from 1 to 300~Hz. Basic parameters of the HRRL are given in the Table~\ref{tab:hrrl-par}. As shown in the Fig.~\ref{fig:app-hrrl-cavity}, the HRRL has a thermionic gun, vertical and horizontal steering magnet sets on two ends and two solenoid magnets.
\begin{table} \centering \caption{The Basic Parameters of the HRRL.} \begin{tabular}{lcc} \toprule {Parameter} & {Unit} & {Value} \\ \midrule maximum energy & MeV & 16 \\ peak current & mA & 100 \\ repetition rate & Hz & 300 \\ absolute energy spread & MeV & 2-4 \\ macro pulse length & ns & $>$50 \\ \bottomrule \end{tabular} \label{tab:hrrl-par} \end{table}
\begin{figure} \centering %\includegraphics[scale=0.6]{3-Apparatus/Figures/HRRL_Cavity.eps} \includegraphics[scale=0.6]{3-Apparatus/Figures/HRRL_Cavity3.eps} \caption{The configuration of the HRRL cavity.} \label{fig:app-hrrl-cavity} \end{figure}
The accelerator's cavity was relocated to the position shown in the Fig.~\ref{fig:app-hrrl-line} to provide enough space for a beam line that can transport either positrons or electrons. The beam elements are described in the Table~\ref{tab:app-hrrl-coordinates}. Quadrupole and dipole magnets were added to the new beam line as well as diagnostic tools like OTR and YAG screens, Faraday cups and toroids were installed to measure the electron beam size and the current. Energy slits were installed to control energy/momentum spread of the beam after the first dipole. A retractable tungsten foil target (T1) was placed between the 1st and 2nd triplets and used to produce positrons when the electron beam interacts with it. The room where the HRRL is located is divided by a wall into two parts; the accelerator side and the experimental cell. A beam pipe at the end of the 90 degree beamline goes through a hole on the wall and delivers the beam from the accelerator side to the experimental cell. The positron detection system consisting of two NaI detectors was placed at the end of the beamline in the experimental cell side as shown in the Fig.~\ref{fig:app-hrrl-line}.
\begin{sidewaysfigure} \centering \includegraphics[scale=0.3]{3-Apparatus/Figures/HRRL_line.pdf} \caption{The HRRL beamline layout and parts.} \label{fig:app-hrrl-line} \end{sidewaysfigure}
\begin{table} \centering \caption{The HRRL Beamline Parts and Coordinates.} \begin{tabular}{lll} \toprule {Label} & {Beamline Element} & {Distance from} \\ {} & {} & {Linac Exit (mm)} \\ \midrule Q1 & quadrupole & 335 \\ Q2 & quadrupole & 575 \\ Q3 & quadrupole & 813 \\ T1 & e$^+$ production target & 1204 \\ Q4 & quadrupole & 1763 \\ Q5 & quadrupole & 2013 \\ Q6 & quadrupole & 2250 \\ D1 & dipole & 2680 \\ S1 & OTR screen & 3570 \\ FC1 & Faraday cup & 3740 \\ EnS & energy slit & 3050 \\ S2 & YAG screen & 3410 \\ Q7 & quadrupole & 3275 \\ D2 & dipole & 3842 \\ FC2 & Faraday cup & 4142 \\ Q8 & quadrupole & 4044 \\ Q9 & quadrupole & 4281 \\ Q10 & quadrupole & 4571 \\ T2 & annihilation target & 7381 \\ \bottomrule \end{tabular} \label{tab:app-hrrl-coordinates} \end{table}
\section{The OTR Imaging System} The OTR target is 10~$\mu$m thick aluminum foil with a 1.25 inch diameter. The OTR is emitted in a cone shape with the maximum intensity at an angle of $1/\gamma$ with respect to the reflecting angle of the electron beam~\cite{OTR-Gitter}. Three lenses with 2 inches of diameter are used for the imaging system to avoid optical distortion at lower electron energies. The focal lengths and position of the lenses are shown in the Fig.~\ref{image_sys}. The camera used is a JAI CV-A10GE digital camera with a 767 by 576 pixel area. The images were taken by triggering the camera synchronously with the electron gun. \begin{figure} \centering {\scalebox{0.35} [0.35]{\includegraphics{3-Apparatus/MOPPR087f2.eps}}} {\scalebox{0.40} [0.40]{\includegraphics{3-Apparatus/MOPPR087f3}}} \caption{The OTR imaging system.} \label{image_sys} \end{figure}
\section{Positron Detection} When the electron beam is incident on T1, photon and secondary electrons are created along with positrons. These particles are the main source of noises in the experiment. The positrons were transported to the second tungsten target (T2) which was shielded from noise by the concrete wall and Pb bricks. The setup is shown in the Fig.~\ref{fig:HRRL-pos-det-setup}. A 6-way cross was placed at the end of the beamline to hold T2. The 6-way cross has three 1~mil (0.0254 millimeters) thick stainless steel windows. The two horizontal windows perpendicular to the beamline were for the exiting of the 511~keV photons created during the positron annihilation. The one at the end of the 90 degree beamline was used as the beam exit. Two NaI detectors were placed facing two exit windows to detect the photons produced in T2. A lead brick collimator with 2 inch diameter hole placed between the exit window and NaI detector. A scintillator and a Faraday cup were placed at the end of the beamline and were used to tune the electron and positron beam. When positrons reach T2, they are thermalized and annihilated inside T2. During the thermalization, a positron loses its kinetic energy. When it annihilates with an electron, two 511~keV photons are emitted back to back. Two NaI detectors and accelerator RF pulse are in coincidence mode to detect these back to back scattered 511~keV photons and to eliminate noises.
\begin{figure} \centering \includegraphics[scale=0.50]{3-Apparatus/HRRL_Pos_detection.eps} \caption{The positron detection system: T2 (pink) was placed with 45$^\circ$ angle to the horizontal plane first, then rotated 45$^\circ$ along the vertical axis.} \label{fig:HRRL-pos-det-setup} \end{figure}
\subsection{NaI Detectors}
NaI crystals, shown as in the Fig.~\ref{fig:PMT}, were used to detect 511~keV photons from positron annihilation. Originally, the detectors had pulse lengths around 400~$\mu$s. Resistors and capacitors were added to the PMT bases and pulse length is shorten to less than 1~$\mu$s. The NaI detector has one dynode and one anode outputs. The PMT base configuration of the NaI detector is shown in the Fig.~\ref{fig:PMT_base} and bases made shown in the Fig.~\ref{fig:new_base_made}. The crystal is SAINT-GOBAIN CRYSTAL \& DETECTORS (MOD. 3M3/3) NaI crystal with a dimension of $3"\times3"$. The PMT base takes HV around -1150~V. It takes ADC 5.7~$\mu$s to convert the analog signal to a digital signal. The signal from anode was delayed 6~$\mu$s by a long cable and sent to the ADC. \begin{table} \centering \caption{The Radioactive Sources and Corresponding Photon Peaks.} \begin{tabular}{lccc} \toprule {Radioactive Sources} & Unit & First Peak & Second Peak \\ \midrule Co-60 & keV & 1173 & 1332 \\ Na-22 & keV & 511 & 1275 \\ \bottomrule \end{tabular} \label{tab:Na22_Co60} \end{table}
\begin{figure}
\centering
\includegraphics[scale=0.4]{3-Apparatus/SAINT-GOBAIN_3M33.png}
\caption{The NaI crystal dimension.}
\label{fig:PMT}
\end{figure}
\begin{figure} \centering \includegraphics[scale=0.75]{3-Apparatus/Modified_PMT.png} \caption{The modified PMT base design.} \label{fig:PMT_base} \end{figure}
\begin{figure} \centering \includegraphics[scale=0.13]{3-Apparatus/IAC_NaI.png} \caption{The NaI crystals and new bases.} \label{fig:new_base_made} \end{figure}
The NaI detectors were calibrated using a Na-22 and a Co-60 sources with photon peaks indicated in the Table~\ref{tab:Na22_Co60}. The Fig.~\ref{fig:NaI_Co60_Scope} is the oscilloscope image of Co-60 photon pulses incident on the detector with new PMT. The calibrated NaI detector spectrum of Na-22 and Co-60 sources are shown in the Fig.~\ref{fig:NaI-Calb}. The rms values of the fits on the four peaks shown in the Fig.~\ref{fig:NaI-Calb} are $\sigma_{Na, 511}=18.28\pm0.04$~keV, $\sigma_{Na, 1275}=44.51\pm0.27$~keV, $\sigma_{Co, 1173}=42.49\pm0.24$~keV, and $\sigma_{Co, 1332}=50.30\pm0.39$~keV.
\begin{figure} \centering \includegraphics[scale=0.4]{3-Apparatus/NaI_Co60_Scope.png} \caption{Pulses of the Co-60 source obtained using new PMT. The amplitude of of the pulse is about 60~mV. The rise time of the pulse is larger than 50 ns, and the fall time is larger than 700~ns.} \label{fig:NaI_Co60_Scope} \end{figure}
\begin{figure} \centering \includegraphics[scale=0.75]{3-Apparatus/Figures/NaI_Calbration/NaI_Calb1.eps} \caption{The calibrated NaI spectrum of Na-22 and Co-60 sources.} \label{fig:NaI-Calb} \end{figure}
\subsection{Trigger for The DAQ}
The trigger for the DAQ requires a coincidence between two NaI detectors and the electron accelerator gun pulse. The last dynode signals from left and right NaI detectors were inverted using a ORTEC 474 amplifier and sent to a CAEN Mod. N842 Constant Fraction Discriminator (CFD). The RF noise from the accelerator was as large as the signal from the NaI detector. Since it was correlated in time with the gun pulse, the gun pulse was used to generate a VETO pulse that prevent the CFD from triggering on this RF noise. After this discrimination and RF noise rejection, the discriminated dynode signals were sent to an GG 8000-01 octalgate generator that increased the width of the logic signals and created one larger pulse from multiple smaller pulses. This can prevent multiple pulsing. Then the signals were sent to a LeCroy model 622 quad coincidence to generate coincident signals with the electron gun. These coincident signals sent to the third channel of the GG800-01 octalgete generator to generate coincidence between the two signals from detector and gun trigger as given by \begin{equation} \text{(NaI~Left~\&\&~Gun~Trigger)~\&\&~(NaI~Rgiht~\&\&~Gun~Trigger)}. \end{equation} This is to make sure that there is a trigger only when there are trigger signals from both detectors and the electron gun is firing.
The ADC was set to convert the analog signals from the NaI detectors to digital signals when the electron gun is firing. But the converted date were fast cleared unless there is a veto. The first output of the GG800-01 octalgete generator was sent to the CAEN Mod. N93B dual timer to create the veto that prevent the ADC from fast clearing the converted data. The second output of the GG800-01 octalgete generator was sent to ORTEC Gate \& Delay Generator to be delayed by 6~$\mu$s, a necessary time to convert the analog signal from the anode to digital signal, and was used as the trigger for the DAQ to read data in the ADC.
%When there is a trigger in the ADC, the data in the ADC is read
Simulation
\chapter{Simulation} Simulations were performed using G4beamline~\cite{muonsinc} to study the processes of position generation and transportation. ``G4beamline is a particle tracking and simulation program based on the Geant4~\cite{geant4} toolkit that is specifically designed to easily simulate beamlines and other systems using single-particle tracking." Since the ratio of $e^{+}/e^{-}$ during the positron generation process is very low (on the order of 0.001) and the positron beam loss during the transportation is large, it is necessary to divide the whole process into 3 steps. A new beam event generator is created based on the results of the previous step in the simulation.
The first step generates an electron beam with an energy distribution that was used in the experiment. The electrons were transported by three quadrupoles to T1 in a vacuum and as a result of the interactions of the electrons with T1 positrons were produced. The second step is the transportation of the positrons generated at T1 in the first step to the entrance of the first dipole magnet. The third step is the transportation of the positrons from the entrance of the first dipole magnet to the end of the second dipole, the transportation of the beam from the exit of the second dipole to the T2 target, and the interaction of positrons with T2 and the detection of the resulting 511~keV photon pairs.
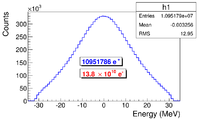
\section{Step 1 - The Electron Beam Generation and Transpiration to T1} In this step, an electron beam is generated with an energy distribution that was used in the experiment. The emittance, the Twiss parameters and the energy distribution of the electron beam were measured experimentally and were used to generate the electron beam in this simulation. The energy distribution of the beam is shown in the Fig.~\ref{fig:En-Scan} in the experiment chapter. The blue dots are measurements and the red line is the fit composed of two skewed Gaussian distributions. The fit parameters are given in the Table~\ref{tab:En-Scan_resluts} in the experiment chapter.
A series of virtual detectors are placed along the beamline to sample the beam. As an example, three detectors and T1 are shown in the Fig.~\ref{fig:T1_UpD_DwD2}. The electron beam is detected by DUPT1 (Detector 25.52~mm UPstream of T1). Positrons, electrons, and photons were generated during the interaction of the electron beam with T1 are observed at DT1 (Detector of T1) and DDNT1 (detector DowN 25.52~mm stream of T1). %In the Fig.~\ref{fig:SimS1_pos_En_DDNT1}, $13.8 \times 10^{10}$ electrons shot at T1 and generated positrons positrons shown in blue.
\begin{figure} \centering \includegraphics[scale=0.50]{4-Simulation/Figures/sim_setup_T1_UpD_DwD2.png} \caption{T1 is positron production target with same geometry and material as the real target. DUPT1 is a virtual detector located upstream of T1 to sample the incoming electron beam. DDNT1 is a down stream virtual detector. DT1 is a virtual detector that is placed right after T1 parallel to it.} \label{fig:T1_UpD_DwD2} \end{figure}
\subsection{The Positron Beam on DDNT1}
In the simulation, $1.38 \times 10^{10}$ (13799743900) electrons, as shown by the black line in the Fig.~\ref{fig:SimS1_T1UPDN}, incident on T1 and created positrons represented by red the line. The blue line is the electrons that were detected downstream of T1. In the Fig.~\ref{fig:SimS1_T1UPDN}, 1000th of the total number of particles are shown due to the large size. The incident electrons were detected by the virtual detector DUPT1 and downstream positrons and electrons were detected by the DDNT1.
\begin{figure} \centering \includegraphics[scale=0.80]{4-Simulation/Figures/s/s1/overlay.eps} \caption{Energy distribution of incident electrons (black), electrons after T1 (blue) and created positrons (red).} \label{fig:SimS1_T1UPDN} \end{figure}
\begin{figure} \begin{tabular}{cc} {\scalebox{0.4} [0.4]{\includegraphics{4-Simulation/Figures/X_e+_DDNT1.eps}}} & {\scalebox{0.4} [0.4]{\includegraphics{4-Simulation/Figures/Y_e+_DDNT1.eps}}} \\ (a) $x$ projection. & (b) $y$ projection. \\ {\scalebox{0.4} [0.4]{\includegraphics{4-Simulation/Figures/XP_e+_DDNT1.eps}}} & {\scalebox{0.4} [0.4]{\includegraphics{4-Simulation/Figures/YP_e+_DDNT1.eps}}} \\ (c) $x$ projection of the divergence. & (d) $y$ projection of the divergence.\\ {\scalebox{0.42} [0.4]{\includegraphics{4-Simulation/Figures/XY_e+_DDNT1.png}}} & {\scalebox{0.42} [0.4]{\includegraphics{4-Simulation/Figures/XY_e+_DDNT1_zoom.eps}}} \\ (e) The transverse beam profile. & (f) The transverse beam profile zoomed in. \\ \end{tabular} \caption{The transverse beam projections and angular distributions of positrons detected.} \label{fig:DDNT1_results} \end{figure}
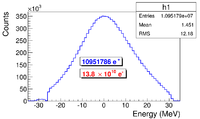
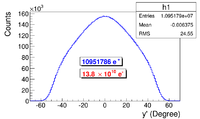
As can be seen from the Fig.~\ref{fig:DDNT1_results} (b) and (d), the $y$ spatial distribution and divergence of the positron beam have a sharp drop in counts on the left. The $y$ $vs.$ $x$ distribution of the beam is shown in the Fig.~\ref{fig:DDNT1_results}~(e) and the Fig.~\ref{fig:DDNT1_results} (f) is zoomed in version of it. The drop in counts is in the interval between $-25.8$~mm and $-27.2$~mm from the center of the target. The Fig.~\ref{fig:sim-DDNT1-T1-geo} shows the geometry of T1 and the relative location of DDNT1 to it. If the size of T1 were to be increased, it would eventually intersect with DDNT1 at a distance between $25.8$~mm and $27.2$~mm from the beam center, $i.e.$ the edge of the T1 is facing this $1.4$~mm wide low count area. %This is the result of the target's thickness of 1.016 mm and the 45$^{\circ}$ angle of intersection ($1.016\sqrt{2}=1.44$). The edge of the target does not produce many positrons compared to the face of the target. \begin{figure} \centering %\includegraphics[scale=0.18]{4-Simulation/Figures/sim-DDNT1-T1-geo.png} \includegraphics[scale=0.9]{4-Simulation/Figures/sharp_drop2.eps} \caption{The geometry of the target T1 and the virtual detector DDNT1.} \label{fig:sim-DDNT1-T1-geo} \end{figure}
As shown in the Fig.~\ref{fig:DDNT1_YpY}, the counts in $y$ distribution decreases at $\theta$ = 45$^{\circ}$. Positrons are emitted from both the downstream and upstream side of T1. Positrons from the downstream side of T1 intersect the detector at angles below 45$^{\circ}$ while positrons from the upstream side of T1 begin to hit the detector at angles beyond 45$^{\circ}$. Neither positrons upstream the downstream of T1 can travel to the 1.4~mm wide low count area, but only positrons created on the edge of T1 can. Thus the counts in this area is lower comparatively.
\begin{figure} \begin{tabular}{cc} {\scalebox{0.4} [0.4]{\includegraphics{4-Simulation/Figures/STSimS1_YYP_DDNT1.png}}} & {\scalebox{0.4} [0.4]{\includegraphics{4-Simulation/Figures/STSimS1_YYP_DDNT1_zoom.png}}} \\ (a) y' $vs.$ y. & (b) y' $vs.$ y zoom. \\ \end{tabular} \caption{The positron beam $y'$ $vs$. $y$ detected by DDNT1.} \label{fig:DDNT1_YpY} \end{figure}
\subsection{The Positron Beam on Virtual Detectors DQ4 and DD1}
The positron beam energy distribution on virtual detectors DQ4 (Detector placed at the entrance of Q4) and DD1UP (Detector placed at the entrance of D1) are shown in the Fig.~\ref{STSimS1_En_DQ4_DD1}. Nearly 90\% of positrons are lost when transported from DQ4 to DD1UP due to the large divergence of positrons. %484.4 mm from T1 to DQ4. 1476.4 mm from T1 to DD1UP. 992 mm from DQ4 to DD1UP.
\begin{figure} \begin{tabular}{ccc} \centerline{\scalebox{0.6} [0.6]{\includegraphics{4-Simulation/Figures/En_e+_DQ4.eps}}} \\ (a) The positron energy distribution on DQ4. \\ \centerline{\scalebox{0.6} [0.6]{\includegraphics{4-Simulation/Figures/En_e+_DD1.eps}}}\\ (b) The positron energy distribution on DD1. \\ \end{tabular} \caption{The positron beam energy distribution detected downstream of T1.} \label{STSimS1_En_DQ4_DD1} \end{figure}
\section{Step 2 - The Transportation of The Positron Beam from DDNT1 to The Entrance of The First Dipole}
In this step, the beam source file is generated by sampling the beam on the virtual detector located downstream of T1 (DDNT1) in previous step. Positrons generated are divided into 1~keV/c momentum bins, since higher energy positrons tend to have smaller polar angles and vise versa. Because of this correlation, the positrons in different momentum bins have different angular distributions. Keeping this correlation in mind, the spatial and angular distribution of the each momentum bin is sampled individually. Each momentum bin generates positrons with different weights, spatial and angular distributions. The positrons are generated at the downstream of T1 (at detector DDNT1) and transported to the entrance of D1 as shown in the Fig~\ref{fig:STSimSetupS2}. The virtual detectors are placed at the entrance of Q4 (DQ4) and D1 (DD1UP) to track the positrons. The beam detected by the DD1UP is sampled for the generation of the positrons in the third step.
\begin{figure} \centering \includegraphics[scale=0.60]{4-Simulation/Figures/STSimSetupS2_2.png} \caption{The magnets and the virtual detectors used in the step 2.} \label{fig:STSimSetupS2} \end{figure}
%\section{Comparing Positrons in Step 1 and Step 2} % %Positrons generated in step 1 and step 2 detected on the virtual detector located at the entrance of the first dipole is compared to validate the positrons generated in the step 2 is similar to the beam in step 1. Results, given in the Fig.~\ref{fg:sim-s1s2-comp-en},~\ref{fg:sim-s1s2-comp-xy},~\ref{fg:sim-s1s2-comp-xpyp}, show that the beam regenerated in step 2 seems is similar to the one in step 1. % %\begin{figure} %\begin{tabular}{cc} %\centerline{\scalebox{0.6} [0.6]{\includegraphics{4-Simulation/Figures/s/s1/EnDD1.eps}}} \\ %(a) Beam Energy in step 1\\ % \\ %\centerline{\scalebox{0.6} [0.6]{\includegraphics{4-Simulation/Figures/s/s2/EnDD1.eps}}}\\ %(b) Beam Energy in step 2\\ %\end{tabular} %\caption{Comparison of positron energy in first and second steps at virtual detector located at the entrance of first dipole.} %\label{fg:sim-s1s2-comp-en} %\end{figure} % %\begin{sidewaysfigure} %\begin{tabular}{cc} %{\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s1/xDD1.eps}}} & {\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s2/xDD1.eps}}} \\ %(a) Beam X-projection in step 1 & (b) Beam X-projection in step 2 \\ %{\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s1/yDD1.eps}}} & {\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s2/yDD1.eps}}} \\ %(c) Beam Y-projection in step 1 & (d) Beam Y-projection in step 2 \\ %\end{tabular} %\caption{Comparison of positron transverse beam profile in first and second steps at virtual detector located at the entrance of first dipole.} %\label{fg:sim-s1s2-comp-xy} %\end{sidewaysfigure} % %\begin{sidewaysfigure} %\begin{tabular}{cc} %{\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s1/xPDD1.eps}}} & {\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s2/xPDD1.eps}}} \\ %(c) Beam divergence X-projection in step 1& (d) Beam divergence X-projection in step 2\\ %{\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s1/yPDD1.eps}}} & {\scalebox{0.5} [0.6]{\includegraphics{4-Simulation/Figures/s/s2/yPDD1.eps}}} \\ %(e) Beam divergence Y-projection in step 1 & (f) Beam divergence Y-projection in step 2 \\ %\end{tabular} %\caption{Comparison of positron transverse divergence in first and second steps at virtual detector located at the entrance of first dipole.} %\label{fg:sim-s1s2-comp-xpyp} %\end{sidewaysfigure}
\section{Step 3 - The Transportation of Positrons from the Entrance of The First Dipole to T2 and The Detection of 511~keV Photons}
In this step, the positrons are generated at the entrance of the first dipole (at DD1UP as shown in the Fig.~\ref{fig:STSimSetupS2}). The beam source file is generated by sampling the beam at DD1UP in the second step. The beam then is transported down to T2 located at the end of the beamline as shown in the Fig.~\ref{fig:T2}. Two virtual detectors with 48~mm diameter (48~mm is the inner diameter of the beam pipe) are placed upstream and downstream of T2 to detect positrons reach to the end of the beamline. Two other virtual detectors with the same diameters as T2 are placed parallel to T2 at two sides of T2 to detect positrons reach T2 and particles after it. The NaI virtual detectors are placed horizontally at two sides and 170~mm away from the beamline center to detect photons. 2 inches thick Pb shielding bricks are placed around NaI detectors with 2-inch diameter circular openings facing T2. When a positron annihilates inside T2, two back-to-back scattered 511~keV photons are generated with the same event number. When both NaI detectors detect 511~keV photons with a same event number, 1 event is registered which indicates one positron is being annihilated inside T2. %The NaI detectors register 1 event when they both detect 511~keV photons with same event number which indicates one positron is being annihilated inside T2.
\begin{figure} \centering \includegraphics[scale=0.4]{4-Simulation/Figures/HRRL_T2.png} \caption{T2 and virtual detectors located upstream (DT2UP) and downstream (DT2DN) of T2 are shown at the center of the figure. NaI detectors and Pb shielding are located horizontally at two sides.} \label{fig:T2} \end{figure}
\subsection{Positrons Detected by The Detection System}
The detector efficiency chart shown in the Fig.~\ref{fig:NaI_Ef}, obtained from SAINT-GOBIAN CRYSTALS~\cite{NaI-Eff}, indicates NaI crystals has 68\% efficiency for 511~keV photons. If two detectors are operated in coincidence mode, the detection efficiency of the system should be the multiplication of the individual two detectors, $i.e.$ $68\% \times 68\%~=~46.24\%$. The Fig.~\ref{fig:e+_Generated_and_Detected} shows the counts of 511~keV photon pairs detected (after multiplied to 46.24\% efficiency) overlaid with the positrons that are detected on DDNT1.
\begin{figure} \centering \includegraphics[scale=0.60]{4-Simulation/Figures/NaI_Ef_3.png} \caption{NaI detector efficiency obtained from SAINT-GOBIAN CRYSTALS~\cite{NaI-Eff}.} \label{fig:NaI_Ef} \end{figure}
\begin{figure} \centering \includegraphics[scale=0.70]{4-Simulation/Figures/overlay/e+_Generated_and_Detected.eps} \caption{Positrons detected on virtual detector DDNT1 and 511~keV photon pairs detected by the NaI detectors in coincidence mode when Q7 is at 0~A, 3.5~A and 10~A.} \label{fig:e+_Generated_and_Detected} \end{figure}
%\begin{figure} %\centering %\includegraphics[scale=0.70]{4-Simulation/Figures/S2E/S2E.eps} %\caption{Results of simulation of positron generation and transportation process.} %\label{fig:S2E} %\end{figure} % % %\begin{sidewaysfigure} %\centering %\includegraphics[scale=1.2]{4-Simulation/Figures/S2E/S2E_32.eps} %\caption{Results of simulation of positron generation and transportation process.} %\label{fig:S2E_32} %\end{sidewaysfigure}
\subsection{Beam Loss Study}
%In this step, 14,359,380,000 positrons generated at DD1. By using the DQ4 and DDNT1 to DD1 ratios of we obtained from previous two steps, one can calculate that it is equivalent generating 57,559,974,511,209.3 at DDNT1, and detecting 375,891,831,521 at DQ4 and 14,359,380,000 at DD1 (i.e. DDNT1:57,559,974,511,209->DQ4:375,891,831,521->DD1:14,359,380,000). %Positrons are generated by $7.2528135 \times 10^{16}$ electrons incident on T1. $5.7559974511209 \times 10^{13}$ As mentioned above, the whole simulation process is divided into three steps by sampling the beam at certain points and generating the beam at same point with a greater number of particles. As the result of the increasing of the number of particles at the second and third steps, as if there were $7.253 \times 10^{16}$ electrons incident on the T1 created $5.756 \times 10^{13}$ positrons at the first step. Positrons detected along the beamline are shown in the Table~\ref{tab:app-hrrl-par} and the Fig.~\ref{fig:TransEff}. 511~keV photon pairs were detected by NaI detectors in coincidence mode are shown in the last column of the Table~\ref{tab:app-hrrl-par}.
\begin{sidewaystable} \centering \caption{Predicted Number of Positrons Transported and Number of 511~keV Photons Detected.} \begin{tabular}{lccccccccc} %\begin{tabular}{lllllllllll} \toprule Energy & On & Enter & Enter & Exit & Enter & Enter & Exit & Reach & $\gamma$ on \\ (MeV) & DDNT1 & Q4 & D1 & D1 & Q7 & D2 & D2 & T2 & NaI \\ \midrule %$1.02 \pm 0.25$ & $2.53 \times 10^{12} $ & $1.36 \times 10^{10} $ & $1.37 \times 10^{9} $ & $1.21 \times 10^{8}$ & $2.61 \times 10^{7} $ & $2.73 \times 10^{6} $ & $1.18 \times 10^{6} $ & $1.07 \times 10^{4} $ & $6$\\ %$1.50 \pm 0.25$ & $4.92 \times 10^{12} $ & $2.75 \times 10^{10} $ & $2.76 \times 10^{9} $ & $1.76 \times 10^{8}$ & $9.06 \times 10^{7} $ & $2.72 \times 10^{7} $ & $1.19 \times 10^{7} $ & $1.40 \times 10^{5} $ & $53 $\\ %$2.15 \pm 0.25$ & $6.47 \times 10^{12} $ & $3.76 \times 10^{10} $ & $3.77 \times 10^{9} $ & $3.80 \times 10^{8}$ & $1.73 \times 10^{8} $ & $7.77 \times 10^{7} $ & $3.59 \times 10^{7} $ & $9.58 \times 10^{6} $ &$477 $\\ %$2.50 \pm 0.25$ & $6.80 \times 10^{12} $ & $4.05 \times 10^{10} $ & $4.07 \times 10^{9} $ & $4.43 \times 10^{8}$ & $2.33 \times 10^{8} $ & $1.06 \times 10^{8} $ & $5.03 \times 10^{7} $ & $1.19 \times 10^{6} $ & $517 $\\ %$3.00 \pm 0.25$ & $6.63 \times 10^{12} $ & $4.08\times 10^{10} $ & $4.09 \times 10^{9} $ & $4.56 \times 10^{8}$ & $2.69 \times 10^{8} $ & $1.26 \times 10^{8} $ & $6.14 \times 10^{7} $ & $1.20 \times 10^{6} $ & $488 $\\ %$3.50 \pm 0.25$ & $6.11 \times 10^{12} $ & $3.89 \times 10^{10} $ & $3.90 \times 10^{9} $ & $4.40 \times 10^{8}$ & $2.80 \times 10^{8} $ & $1.36 \times 10^{8} $ & $6.74 \times 10^{7} $ & $1.19 \times 10^{6} $ & $474 $\\ %$4.02 \pm 0.25$ & $5.34 \times 10^{12} $ & $3.51 \times 10^{10} $ & $3.52 \times 10^{9} $ & $4.05 \times 10^{8}$ & $2.70 \times 10^{8} $ & $1.38 \times 10^{8} $ & $6.89 \times 10^{7} $ & $1.16 \times 10^{6} $ & $472 $\\ %$4.50 \pm 0.25$ & $4.58 \times 10^{12} $ & $3.10 \times 10^{10} $ & $3.11 \times 10^{9} $ & $3.58 \times 10^{8}$ & $2.47 \times 10^{8} $ & $1.30 \times 10^{8} $ & $6.66 \times 10^{7} $ & $1.10 \times 10^{6} $ &$ 444 $\\ %$5.00 \pm 0.25$ & $3.77 \times 10^{12} $ & $2.65 \times 10^{10} $ & $2.67 \times 10^{9} $ & $3.09 \times 10^{8}$ & $2.19 \times 10^{8} $ & $1.19 \times 10^{8} $ & $6.22 \times 10^{7} $ & $1.01 \times 10^{6} $ & $392 $\\ %$5.50 \pm 0.25$ & $3.01 \times 10^{12} $ & $2.21 \times 10^{10} $ & $2.21 \times 10^{9} $ & $2.60 \times 10^{8}$ & $1.87 \times 10^{8} $ & $1.04 \times 10^{8} $ & $5.57 \times 10^{7} $ & $9.07 \times 10^{5} $ & $354 $\\
%$1.02 \pm 0.25$ & $2.53 \times 10^{12} $ & $1.36 \times 10^{10} $ & $1.37 \times 10^{9} $ & $1.21 \times 10^{8}$ & $2.61 \times 10^{7} $ &$2.53 \times 10^{7} $ & $2.73 \times 10^{6} $ & $1.18 \times 10^{6} $ & $1.07 \times 10^{4} $ & $6$\\ %$1.50 \pm 0.25$ & $4.92 \times 10^{12} $ & $2.75 \times 10^{10} $ & $2.76 \times 10^{9} $ & $1.76 \times 10^{8}$ & $9.06 \times 10^{7} $ &$8.64 \times 10^{7} $ & $2.72 \times 10^{7} $ & $1.19 \times 10^{7} $ & $1.40 \times 10^{5} $ & $53 $\\ %$2.15 \pm 0.25$ & $6.47 \times 10^{12} $ & $3.76 \times 10^{10} $ & $3.77 \times 10^{9} $ & $3.80 \times 10^{8}$ & $1.73 \times 10^{8} $ &$1.65 \times 10^{8} $ & $7.77 \times 10^{7} $ & $3.59 \times 10^{7} $ & $9.58 \times 10^{6} $ &$477 $\\ %$2.50 \pm 0.25$ & $6.80 \times 10^{12} $ & $4.05 \times 10^{10} $ & $4.07 \times 10^{9} $ & $4.43 \times 10^{8}$ & $2.33 \times 10^{8} $ &$2.20 \times 10^{8} $ & $1.06 \times 10^{8} $ & $5.03 \times 10^{7} $ & $1.19 \times 10^{6} $ & $517 $\\ %$3.00 \pm 0.25$ & $6.63 \times 10^{12} $ & $4.08\times 10^{10} $ & $4.09 \times 10^{9} $ & $4.56 \times 10^{8}$ & $2.69 \times 10^{8} $ &$2.52 \times 10^{8} $ & $1.26 \times 10^{8} $ & $6.14 \times 10^{7} $ & $1.20 \times 10^{6} $ & $488 $\\ %$3.50 \pm 0.25$ & $6.11 \times 10^{12} $ & $3.89 \times 10^{10} $ & $3.90 \times 10^{9} $ & $4.40 \times 10^{8}$ & $2.80 \times 10^{8} $ &$2.64 \times 10^{8} $ & $1.36 \times 10^{8} $ & $6.74 \times 10^{7} $ & $1.19 \times 10^{6} $ & $474 $\\ %$4.02 \pm 0.25$ & $5.34 \times 10^{12} $ & $3.51 \times 10^{10} $ & $3.52 \times 10^{9} $ & $4.05 \times 10^{8}$ & $2.70 \times 10^{8} $ &$2.56 \times 10^{8} $ & $1.38 \times 10^{8} $ & $6.89 \times 10^{7} $ & $1.16 \times 10^{6} $ & $472 $\\ %$4.50 \pm 0.25$ & $4.58 \times 10^{12} $ & $3.10 \times 10^{10} $ & $3.11 \times 10^{9} $ & $3.58 \times 10^{8}$ & $2.47 \times 10^{8} $ &$2.36 \times 10^{8} $ & $1.30 \times 10^{8} $ & $6.66 \times 10^{7} $ & $1.10 \times 10^{6} $ &$ 444 $\\ %$5.00 \pm 0.25$ & $3.77 \times 10^{12} $ & $2.65 \times 10^{10} $ & $2.67 \times 10^{9} $ & $3.09 \times 10^{8}$ & $2.19 \times 10^{8} $ &$2.10 \times 10^{8} $ & $1.19 \times 10^{8} $ & $6.22 \times 10^{7} $ & $1.01 \times 10^{6} $ & $392 $\\ %$5.50 \pm 0.25$ & $3.01 \times 10^{12} $ & $2.21 \times 10^{10} $ & $2.21 \times 10^{9} $ & $2.60 \times 10^{8}$ & $1.87 \times 10^{8} $ &$1.80 \times 10^{8} $ & $1.04 \times 10^{8} $ & $5.57 \times 10^{7} $ & $9.07 \times 10^{5} $ & $354 $\\
%$1.02 \pm 0.25$ & $2.5 \times 10^{12} $ & $1.4 \times 10^{10} $ & $1.4 \times 10^{9} $ & $1.2 \times 10^{8}$ & $2.6 \times 10^{7} $ &$2.5 \times 10^{7} $ & $2.7 \times 10^{6} $ & $1.2 \times 10^{6} $ & $1.1 \times 10^{4} $ & $6$\\ %$1.50 \pm 0.25$ & $4.9 \times 10^{12} $ & $2.8 \times 10^{10} $ & $2.8 \times 10^{9} $ & $1.8 \times 10^{8}$ & $9.1 \times 10^{7} $ &$8.6 \times 10^{7} $ & $2.7 \times 10^{7} $ & $1.2 \times 10^{7} $ & $1.4 \times 10^{5} $ & $53 $\\ %$2.15 \pm 0.25$ & $6.5 \times 10^{12} $ & $3.8 \times 10^{10} $ & $3.8 \times 10^{9} $ & $3.8 \times 10^{8}$ & $1.7 \times 10^{8} $ &$1.7 \times 10^{8} $ & $7.8 \times 10^{7} $ & $3.6 \times 10^{7} $ & $9.6 \times 10^{6} $ & $477 $\\ %$2.50 \pm 0.25$ & $6.8 \times 10^{12} $ & $4.1 \times 10^{10} $ & $4.1 \times 10^{9} $ & $4.4 \times 10^{8}$ & $2.3 \times 10^{8} $ &$2.2 \times 10^{8} $ & $1.1 \times 10^{8} $ & $5.0 \times 10^{7} $ & $1.2 \times 10^{6} $ & $517 $\\ %$3.00 \pm 0.25$ & $6.6 \times 10^{12} $ & $4.1\times 10^{10} $ & $4.1 \times 10^{9} $ & $4.6 \times 10^{8}$ & $2.7 \times 10^{8} $ &$2.5 \times 10^{8} $ & $1.3 \times 10^{8} $ & $6.1 \times 10^{7} $ & $1.2 \times 10^{6} $ & $488 $\\ %$3.50 \pm 0.25$ & $6.1 \times 10^{12} $ & $3.9 \times 10^{10} $ & $3.9 \times 10^{9} $ & $4.4 \times 10^{8}$ & $2.8 \times 10^{8} $ &$2.6 \times 10^{8} $ & $1.4 \times 10^{8} $ & $6.7 \times 10^{7} $ & $1.2 \times 10^{6} $ & $474 $\\ %$4.02 \pm 0.25$ & $5.3 \times 10^{12} $ & $3.5 \times 10^{10} $ & $3.5 \times 10^{9} $ & $4.1 \times 10^{8}$ & $2.7 \times 10^{8} $ &$2.6 \times 10^{8} $ & $1.4 \times 10^{8} $ & $6.9 \times 10^{7} $ & $1.2 \times 10^{6} $ & $472 $\\ %$4.50 \pm 0.25$ & $4.6 \times 10^{12} $ & $3.1 \times 10^{10} $ & $3.1 \times 10^{9} $ & $3.6 \times 10^{8}$ & $2.5 \times 10^{8} $ &$2.4 \times 10^{8} $ & $1.3 \times 10^{8} $ & $6.7 \times 10^{7} $ & $1.1 \times 10^{6} $ & $444 $\\ %$5.00 \pm 0.25$ & $3.8 \times 10^{12} $ & $2.7 \times 10^{10} $ & $2.7 \times 10^{9} $ & $3.1 \times 10^{8}$ & $2.2 \times 10^{8} $ &$2.1 \times 10^{8} $ & $1.2 \times 10^{8} $ & $6.2 \times 10^{7} $ & $1.0 \times 10^{6} $ & $392 $\\ %$5.50 \pm 0.25$ & $3.0 \times 10^{12} $ & $2.2 \times 10^{10} $ & $2.2 \times 10^{9} $ & $2.6 \times 10^{8}$ & $1.9 \times 10^{8} $ &$1.8 \times 10^{8} $ & $1.0 \times 10^{8} $ & $5.6 \times 10^{7} $ & $9.1 \times 10^{5} $ & $354 $\\
$1.02 \pm 0.25$ & $2.5 \times 10^{12} $ & $1.4 \times 10^{10} $ & $1.4 \times 10^{9} $ & $1.2 \times 10^{8}$ & $2.6 \times 10^{7} $ & $2.7 \times 10^{6} $ & $1.2 \times 10^{6} $ & $4.3 \times 10^{3} $ & $7$\\ $1.50 \pm 0.25$ & $4.9 \times 10^{12} $ & $2.8 \times 10^{10} $ & $2.8 \times 10^{9} $ & $1.8 \times 10^{8}$ & $9.1 \times 10^{7} $ & $2.7 \times 10^{7} $ & $1.2 \times 10^{7} $ & $5.1 \times 10^{4} $ & $97 $\\ $2.15 \pm 0.25$ & $6.5 \times 10^{12} $ & $3.8 \times 10^{10} $ & $3.8 \times 10^{9} $ & $3.8 \times 10^{8}$ & $1.7 \times 10^{8} $ & $7.8 \times 10^{7} $ & $3.6 \times 10^{7} $ & $4.4 \times 10^{5} $ & $734 $\\ $2.50 \pm 0.25$ & $6.8 \times 10^{12} $ & $4.1 \times 10^{10} $ & $4.1 \times 10^{9} $ & $4.4 \times 10^{8}$ & $2.3 \times 10^{8} $ & $1.1 \times 10^{8} $ & $5.0 \times 10^{7} $ & $4.6 \times 10^{5} $ & $794 $\\ $3.00 \pm 0.25$ & $6.6 \times 10^{12} $ & $4.1\times 10^{10} $ & $4.1 \times 10^{9} $ & $4.6 \times 10^{8}$ & $2.7 \times 10^{8} $ & $1.3 \times 10^{8} $ & $6.1 \times 10^{7} $ & $4.5 \times 10^{5} $ & $723 $\\ $3.50 \pm 0.25$ & $6.1 \times 10^{12} $ & $3.9 \times 10^{10} $ & $3.9 \times 10^{9} $ & $4.4 \times 10^{8}$ & $2.8 \times 10^{8} $ & $1.4 \times 10^{8} $ & $6.7 \times 10^{7} $ & $4.4 \times 10^{5} $ & $716 $\\ $4.02 \pm 0.25$ & $5.3 \times 10^{12} $ & $3.5 \times 10^{10} $ & $3.5 \times 10^{9} $ & $4.1 \times 10^{8}$ & $2.7 \times 10^{8} $ & $1.4 \times 10^{8} $ & $6.9 \times 10^{7} $ & $4.3 \times 10^{5} $ & $702 $\\ $4.50 \pm 0.25$ & $4.6 \times 10^{12} $ & $3.1 \times 10^{10} $ & $3.1 \times 10^{9} $ & $3.6 \times 10^{8}$ & $2.5 \times 10^{8} $ & $1.3 \times 10^{8} $ & $6.7 \times 10^{7} $ & $4.0 \times 10^{5} $ & $646 $\\ $5.00 \pm 0.25$ & $3.8 \times 10^{12} $ & $2.7 \times 10^{10} $ & $2.7 \times 10^{9} $ & $3.1 \times 10^{8}$ & $2.2 \times 10^{8} $ & $1.2 \times 10^{8} $ & $6.2 \times 10^{7} $ & $3.6 \times 10^{5} $ & $566 $\\ $5.50 \pm 0.25$ & $3.0 \times 10^{12} $ & $2.2 \times 10^{10} $ & $2.2 \times 10^{9} $ & $2.6 \times 10^{8}$ & $1.9 \times 10^{8} $ & $1.0 \times 10^{8} $ & $5.6 \times 10^{7} $ & $3.3 \times 10^{5} $ & $533 $\\ \bottomrule \end{tabular} \label{tab:app-hrrl-par} \end{sidewaystable}
\begin{figure} \centering \includegraphics[scale=0.80]{4-Simulation/Figures/Transporation_Efficiency/Ef.eps} \caption{Predicted number of positrons transported. Black circle: positrons incident on DDNT1. Red circle: positrons entered Q4. Blue circle: positrons entered D1. Magenta circle: positrons exited D1. Black cube: positrons entered Q7. Red cube: positrons entered D2. Blue cube: positrons exited D2. Magenta cube: positrons incident on DT2UP. Black triangle: 511~keV photons detected by NaI detectors in coincidence mode.} \label{fig:TransEff} \end{figure}
As can be seen from the Table~\ref{tab:app-hrrl-par}, the positrons are divided into 10 bins by energy. At detector DDNT1 (25.8~mm after T1), there are about $10^{12}$ positrons in each bin. At the entrance of Q4, the counts drop two orders of magnitude. This can be explained by the solid angle that the entrance of Q4 makes, if one assumes T1 is a point source of positrons. The distance between T1 and the virtual detector DQ4 is $d = 560$~mm and the radius of DQ4 is $r = 24$~mm. The solid angle of the DQ4 is $\Omega_{\text{Q4}}=\frac{\pi r^2}{d^2}=\frac{\pi 24^2}{560^2}$~rad. Positrons make up a cone with a 45$^\circ$ half angle, which is $\Omega_{\text{beam}}=0.6\pi$~rad in solid angle. The ratio of the two solid angles, $\Omega_{\text{Q4}}/\Omega_{\text{beam}}$, is 1:160, $i.e.$ 1 out of 160 positrons make it from T1 to DQ4, given that the positron beam is isotropic inside the cone. However, the positron beam peaks at a smaller angle as shown in the Fig.~\ref{fig:DDNT1_results} (c) and (d) and there are actually more positrons make it from DDNT1 to DQ4, resulting in higher ratio than 1:160. This make the ratio closer to 1:100. % for solid angle integrate sin(\theta)d\theta d\phi, theta=[0,90],phi=[0,360]. % $1.3 \times 10^{8} $ & $6.1 \times 10^{7} $ & $1.2 \times 10^{6} $ & $488 $\\
As an example to explain the beam loss along the beamline, the dipoles were set to transport $1.436 \times 10^9$ (one tenth of the number on the Table~\ref{tab:app-hrrl-par}) 3~MeV positrons at the entrance of D1 as shown in the Fig.~\ref{fig:dipole-trans}. Beam energy distribution was plotted at the exit of D1, entrance of Q7, exit of Q7, entrance of D2, exit of D2, and at T2. $4.1 \times 10^8$ positrons entered and $4.6 \times 10^7$ exited D1, $2.7 \times 10^7$ entered and $2.5 \times 10^7$ exited Q7, $1.3 \times 10^{7} $ entered and $6.1 \times 10^{6} $ exited D2. At the end, $4.5 \times 10^{5}$ positrons reached T2. These positrons produced 256195 511~keV photon pairs inside T2 and 255861 escaped T2.
The distance between NaI detectors and the beamline center is 170~cm. The Pb shielding has a hole facing T2 with 2 inches diameter. Assuming positrons annihilated at the center of T2, the solid angle a NaI detector make is $\Omega=\frac{\pi r^2}{d^2}=\frac{\pi 25.4^2}{170^2}$~rad. The 511~keV photons created during the annihilation make a solid angle of $2\pi$~rad considering each side of T2 is facing one detector. The ratio of $2\pi$~rad to solid angle of T2 is about 90:1.
In a simulation with similar settings as in the Table~\ref{tab:app-hrrl-par}, dipoles are set to bend 3~MeV positrons. As a result, $4.40041\times10^5$ 3~MeV positrons incident on T2 and created 254864 511~keV photon pairs ($i.e.$ 58\% of the positrons annihilated). Two 0.0254~mm thick stainless steel vacuum windows are placed 9~cm from T2 at two sides of the beamline. Detectors are placed in the front and back of vacuum windows to observe their affect on the photons (the detectors are placed 1~$\mu$m from the windows). 4330 511~keV photons went into the vacuum window and 4300 made it through. 0.7\% of photon pairs are lost when passing through the vacuum windows.
The left NaI detector detected 2897 511~keV photons and the right one detected 4100. The ratio of 511~keV photon pairs created in T2 to ones that made it to the right and the left NaI are 88:1 and 62:1 respectively. These are close to the ratios predicted by solid angle ratio 90:1. %The counts on the right detector is little higher than on left detector because the T2 is facing the left side. 1518 511~keV photon pairs are detected by NaI detectors in coincidence mode. The ratio 511~keV photon pairs created to the ones detected in coincidence mode is 168:1. Counting photons in coincidence mode cut the rate by half. Note that these counts are given after considering detection efficiency of the system.
%The energy is 0.001 MeV (1 keV), in the figure at the exit of D1 the counts are from 2.8 MeV to 3.3 MeV, i.e. 500 keV, the amplitude of the peak is $8 \times 10^5$, $500 \times 8 \times 10^5 = 4 \times 10^8$, same as given above.
\begin{figure} \centering \includegraphics[scale=0.70]{4-Simulation/Figures/Transporation_Efficiency/En2.eps} \caption{Positrons transported when dipoles are set to bend 3~MeV positrons.} \label{fig:dipole-trans} \end{figure}
\section{Quadrupole Triplet Collection Efficiency Study}
5,475,869,400 positrons were generated at DDNT1 and transported to DD1 to study quadrupole triplet positron collection and transportation efficiency. Six quadrupole current settings were simulated as shown in the Table~\ref{tab:triplet-eff}. As can be seen, for different quadrupole current settings, no significant differences were observed in the number of positrons, transverse beam profiles and momentum distributions. On average, 3590413 positrons were detected by DD1. The ratio of positrons generated to the ones that enter D1 is 1525:1.
\begin{sidewaystable} \centering \caption{Quadrupole Triplet System Collection and Transportation Efficiency Data.} \begin{tabular}{cccccccccccccc} \toprule Q4 & Q5 & Q6 & Entries & $x$ & $\sigma_{x} $ & y & $\sigma_{y}$ & $P_{x}$ & $\sigma_{P_{x}}$ & $P_{y}$ & $\sigma_{P_{y}}$ & $P_{z}$ & $\sigma_{P_{z}}$ \\ \midrule A & A & A & & mm & mm & mm & mm & MeV & MeV & MeV & MeV & MeV & MeV \\ \midrule -1 & 2 & -1 & 3587220 & -0.005 & 12 & 0.030 & 12 & $~~3.0 \times 10^{-5}$ & 0.0461 & -0.00216 & 0.04553 & 3.848 & 1.875 \\ -2 & 4 & -2 & 3591423 & -0.012 & 12 & 0.049 & 12 & $~~2.2 \times 10^{-5}$ & 0.0461 & -0.00211 & 0.04554 & 3.848 & 1.875 \\ 1 & -2 & 1 & 3591509 & -0.009 & 12 & 0.040 & 12 & $-1.5 \times 10^{-5}$ & 0.0462 & -0.00216 & 0.04557 & 3.849 & 1.876 \\ 1 & 2 & 1 & 3589854 & -0.005 & 12 & 0.034 & 12 & $-1.8 \times 10^{-5}$ & 0.0462 & -0.00216 & 0.04556 & 3.849 & 1.876 \\ 2 & -4 & 2 & 3592977 & -0.007 & 12 & 0.032 & 12 & $-3.3 \times 10^{-6}$ & 0.0462 & -0.00217 & 0.04549 & 3.849 & 1.876 \\ 2 & 4 & 2 & 3589495 & -0.004 & 12 & 0.033 & 12 & $~~3.0 \times 10^{-6}$ & 0.0462 & -0.00218 & 0.04554 & 3.849 & 1.875 \\ % & & & & & & & & & & & & & \\ \bottomrule \end{tabular} \label{tab:triplet-eff} \end{sidewaystable}
\section{Error Study}
Systematic errors in positron counts are estimated by carrying out simulations with different magnet settings as shown in the Table~\ref{tab:sim-error}. The NaI detectors have 46.42\% efficiency in coincidence mode. The 511~keV photons are counted in coincidence mode ($i.e.$ the original counts was multiplied by 46.42\%) and are given in the Table~\ref{tab:sim-error}. The uncertainty of the magnet power supply is 0.1~A. The Max/Min in the table refers to the Maximum/Minimum magnetic filed strength when the magnet coil current is at I$_{\text{max}}$/I$_{\text{min}}$, where I$_{\text{max}}$ = I$_{\text{def}} + 0.1$~A and I$_{\text{min}}$ = I$_{\text{def}} - 0.1$~A. Def refers to the default magnetic field strength of the magnet. The top 3 rows of the table are magnet settings and counts are given in corresponding columns below for the energies given in the left. The fractional error in the 511~keV photon pair counts is calculated by dividing the standard deviation of counts at different settings by the counts in default magnet setting, $i.e.$ $\frac{\text{standard deviation of counts}}{\text{counts in defalt setting}}$.
\begin{sidewaystable}
\centering
\caption{Systematic Error Study: Counts of NaI Detectors\\ in Coincidence Mode for Different Magnet Settings.}
%\begin{tabular}{cccccccccccc}
\begin{tabular}{lllllllllllll}
\toprule
D1 & Max & Min & Max & Min & Max & Max & Min & Min & Def & & \\
Q7 & Def & Def & Def & Def & Max & Min & Min & Def & Def & & \\
D2 & Max & Min & Def & Def & Def & Def & Def & Def & Def & & \\
\midrule
Energy (MeV)& & & & & & & & & & Average & Fractional Error \\
\midrule
0.765~1.265 & 12 & 2 & 3 & 1 & 1 & 3 & 3 & 0 & 6 & 4 & 57.3 \% \\
1.25~-~1.75 & 95 & 75 & 70 & 86 & 85 & 92 & 129 & 86 & 97 & 90 & 17.6 \% \\
1.85~-~2.35 & 674 & 724 & 737 & 769 & 686 & 747 & 803 & 681 & 734 & 728 & 5.8 \% \\
2.25~-~2.75 & 781 & 755 & 753 & 759 & 772 & 963 & 794 & 763 & 794 & 793 & 8.3 \% \\
2.75~-~3.25 & 739 & 737 & 765 & 752 & 738 & 698 & 738 & 757 & 723 & 739 & 2.7 \% \\
3.25~-~3.75 & 713 & 699 & 747 & 712 & 707 & 751 & 718 & 705 & 716 & 719 & 2.5 \% \\
3.77~-~4.27 & 690 & 708 & 715 & 676 & 704 & 658 & 706 & 715 & 701 & 697 & 2.7 \% \\
4.25~-~4.75 & 627 & 666 & 634 & 646 & 635 & 675 & 637 & 653 & 646 & 646 & 2.5 \% \\
4.75~-~5.25 & 558 & 595 & 594 & 603 & 606 & 688 & 582 & 582 & 566 & 597 & 6.7 \% \\
5.25~-~5.75 & 513 & 536 & 535 & 522 & 525 & 535 & 518 & 544 & 533 & 529 & 1.9 \% \\
\bottomrule \end{tabular} \label{tab:sim-error} \end{sidewaystable}
Experiment
\chapter{Experiment}
\section{Quadrupole Scanning Experiment} Quadrupole scanning method is used to perform emittance measurement. The quadrupole current is changed to alter the strength and direction of the quadrupole magnetic field such that a measurable change in the beam shape is seen by the OTR system. Initially, the beam was steered by the quadrupole indicating that the beam was not entering along the quadrupole's central axis. Several magnetic elements upstream of this quadrupole were adjusted to align the incident electron beam with the quadrupole's central axis. First, the beam current observed by a Faraday cup located at the end of beam line was maximized using upstream steering coils within the linac nearest the gun. Second, the first solenoid nearest the linac gun was used to focus the electron beam on the OTR screen. Steering coils were adjusted to maximize the beam current to the Faraday cup and minimize the deflection of the beam by the solenoid first then by the quadrupole. A second solenoid and the last steering magnet shown in Fig~\ref{fig:app-hrrl-cavity}, both near the exit of the linac, were used in the final step to optimize the beam spot size on the OTR target and maximize the Faraday cup current. A configuration was found that minimized the electron beam deflection when the quadrupole current was altered during the emittance measurements.
The emittance measurement was performed using an electron beam energy of 15~MeV and a 200~ns long, macro pulse of 40~mA current. The current in the first quadrupole after the exit of the linac was changed from $-$~5~A to $+$~5~A with an increment of 0.2~A. Seven measurements were taken at each current step in order to determine the average beam width and the variance. Background measurements were taken by turning the linac's electron gun off while keep the RF on. Background image and beam images before and after background subtraction are shown in the Fig.~\ref{bg}. A small dark current is visible in the Fig.~\ref{bg} b that is known to be generated when electrons are pulled off the cavity wall and accelerated.
\begin{figure} \begin{tabular}{ccc} \centerline{\scalebox{0.42} [0.42]{\includegraphics{3-Apparatus/MOPPR087f4.eps}}} \\ (a)\\ \centerline{\scalebox{0.42} [0.42]{\includegraphics{3-Apparatus/MOPPR087f5.eps}}}\\ (b)\\ \centerline{\scalebox{0.42} [0.42]{\includegraphics{3-Apparatus/MOPPR087f6.eps}}}\\ (c) \end{tabular} \caption{Digital image from the OTR screen; (a) a beam with the dark current and background noise, (b) a background image taken when RF is on gun is off, (c) a beam image when dark background was subtracted.} \label{bg} \end{figure}
The electron beam energy was measured using a dipole magnet downstream of the quadrupole used for the emittance measurements. Prior to energizing the dipole, the electron micro-pulse bunch charge passing through the dipole was measured using a Faraday cup located approximately 50~cm downstream of the OTR screen. The dipole current was adjusted until a maximum beam current was observed on another Faraday cup located just after the 45 degree exit port of the dipole. A magnetic field map of the dipole indicates that the electron beam energy was 15~$\pm$~1.6~MeV.
%\subsection{Data Analysis and Results} Images from the JAI camera were calibrated using the OTR target frame. An LED was used to illuminate the OTR aluminum frame that has a known inner diameter of 31.75~mm. Image processing software was used to inscribe a circle on the image to measure the circular OTR inner frame in units of pixels. The scaling factor can be obtained by dividing this length with the number of pixels observed. The result is a horizontal scaling factor of 0.04327~$\pm$~0.00016~mm/pixel and vertical scaling factor of 0.04204~$\pm$~0.00018~mm/pixel. Digital images from the JAI camera were extracted in a matrix format in order to take projections on both axes and perform a Gaussian fit. The observed image profiles were not well described by a single Gaussian distribution. The profiles may be described using a Lorentzian distribution, however, the rms of the Lorentzian function is not defined. A super Gaussian distribution was used~\cite{sup-Gau}, because rms values may be directly extracted. The Chi-square for x and y profiles are $2.4 \times 10^7$ and $1.9 \times 10^7$ for super Gaussian fit and $2.6 \times 10^8$ and $9.1 \times 10^7$ Gaussian fit. The beam spot, beam projections and fits are shown in the Fig.~\ref{Gau-SupGaus-fits}. In Gaussian distribution, $\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$, $x$ on exponent is raised to the 2nd power. In the super Gaussian distribution, $x$ on exponent is smaller than 2, resulting a sharper peak than Gaussian distribution. In Fig.~\ref{Gau-SupGaus-fits} the super Gaussian fits raised $x$ on exponent to $N_{x} = 0.9053$ and $N_{y} = 1.0427$.
\begin{figure} \begin{tabular}{cc} {\scalebox{0.42} [0.4]{\includegraphics{5-Experiment/Figures/Gau_SupGau/Gau_ChiSqaure.eps}}} {\scalebox{0.42} [0.4]{\includegraphics{5-Experiment/Figures/Gau_SupGau/SupGau_ChiSqaure.eps}}} \end{tabular} \caption{Gaussian and super Gaussian fits for beam projections. The beam images is background subtracted image and taken when quadrupole magnets are turned off. Left image is Gaussian fit and right image is super Gaussian fit.} \label{Gau-SupGaus-fits} \end{figure}
Fig.~\ref{fig:par-fit} shows the square of the rms ($\sigma^2_{\textnormal{s}}$) $vs$ $k_1L$ for $x$ (horizontal) and $y$ (vertical) beam projections along with the parabolic fits using Eq.~\ref{fig:par-fit}. The emittance and Twiss parameters from these fits are summarized in Table~\ref{tab:results}. MATLAB scripts used to calculate emittance and Twiss parameters are given in appendix B. \begin{figure} \begin{tabular}{cc} {\scalebox{0.295} [0.295]{\includegraphics{3-Apparatus/par_fit_x.eps}}} {\scalebox{0.295} [0.295]{\includegraphics{3-Apparatus/par_fit_y.eps}}} \end{tabular} \caption{Square of rms values and parabolic fittings.} \label{fig:par-fit} \end{figure}
\begin{table} \centering \caption{Emittance Measurement Results} \begin{tabular}{lcc} \toprule {Parameter} & {Unit} & {Value} \\ \midrule projected emittance $\epsilon_x$ & $\mu$m & $0.37 \pm 0.02$ \\ projected emittance $\epsilon_y$ & $\mu$m & $0.30 \pm 0.04$ \\ % normalized \footnote{normalization procedure assumes appropriate beam chromaticity.} emittance $\epsilon_{n,x}$ & $\mu$m & $10.10 \pm 0.51$ \\ %normalized emittance $\epsilon_{n,y}$ & $\mu$m & $8.06 \pm 1.1$ \\ $\beta_x$-function & m & $1.40 \pm 0.06$ \\ $\beta_y$-function & m & $1.17 \pm 0.13$ \\ $\alpha_x$-function & rad & $0.97 \pm 0.06$ \\ $\alpha_y$-function & rad & $0.24 \pm 0.07$ \\ micro-pulse charge & pC & 11 \\ micro-pulse length & ps & 35 \\ energy of the beam $E$ & MeV & 15 $\pm$ 1.6 \\ relative energy spread $\Delta E/E$ & \% & 10.4 \\ \bottomrule \end{tabular} \label{tab:results} \end{table}
\section{Energy Scan} The energy profile of HRRL was measured when it was tuned to accelerate electrons to 12~MeV peak energy. A Faraday cup was placed at the end of the 45 degree beamline to measure the electron beam current when D1 was on and D2 was off. Dipole coil current was changed in 1~A increment and the electron beam current with corresponding energy observed using Faraday cup. The relation between dipole coil current and the beam energy is given in the appendix A. As shown in the Fig.~\ref{fig:En-Scan}, a 12~MeV peak was observed with a long low energy tail. The energy distribution of HRRL can be described by overlapping two skewed Gaussian fits~\cite{sup-Gau}. The fit function is given by \begin{equation} G(En) = A_{1}e^{\frac{-(En-\mu_{1})^2}{2(\sigma_{1}(1+sign(En-\mu_{1}))E_{1})^2}} + A_{2}e^{\frac{-(En-\mu_{2})^2}{2(\sigma_{2}(1+sign(En-\mu_{2}))E_{2})^2}}, \label{eq:skew-Gau} \end{equation} where $\sigma_{1}=\frac{\sigma_{r,1}+\sigma_{l,1}}{2}$, $\sigma_{2}=\frac{\sigma_{r,2}+\sigma_{l,2}}{2}$, $E_{1}=\frac{\sigma_{r,1}-\sigma_{l,1}}{\sigma_{r,1}+\sigma_{l,1}}$, and $E_{2}=\frac{\sigma_{r,2}-\sigma_{l,2}}{\sigma_{r,2}+\sigma_{l,2}}$. The measurement results and fits are shown in the Fig.~\ref{fig:En-Scan} and in the Table~\ref{tab:En-Scan_resluts}.
\begin{figure} \centering \includegraphics[scale=0.50]{3-Apparatus/En_Fit_Assym_Gau.eps} \caption{HRRL energy scan (blue dots) and fit (red line) with two skewed Gaussian distribution.} \label{fig:En-Scan} \end{figure}
\begin{table} \centering \caption{Fit Parameters for Two Skewed Gaussian.} \begin{tabular}{llcc} \toprule {Parameter} & Unit & {First Gaussian} & {Second Gaussian} \\ \midrule amplitude A & mA & ~2.14 & 10.88 \\ mean $\mu$ & MeV & 12.07 & 12.32 \\ sigma left $\sigma_L$ & MeV & ~4.47 & ~0.70 \\ sigma right $\sigma_R$ & MeV & ~1.20 & ~0.45 \\ \bottomrule \end{tabular} \label{tab:En-Scan_resluts} \end{table}
\section{The Positron Production Runs}
The annihilation target T2 is a tungsten foil that can be inserted or removed from the center of the beamline. This configuration allows two kinds of runs, T2 in and T2 out. When T2 is in, the positions are delivered to T2. The positrons thermalize and annihilate, then produce 511~keV photons. These photons are detected by two NaI detectors as shown in the Fig.~\ref{fig:HRRL-En-Scan}. When T2 is out, positrons exit the beamline and reach the beam dump. NaI detectors are shielded with Pb bricks from the beam dump. T2 out runs are used as the background measurements.
\begin{figure} \centering \includegraphics[scale=0.50]{3-Apparatus/NaI_Setup4.png} \caption{Positron detection using T2 and NaI detectors.} \label{fig:HRRL-En-Scan} \end{figure}
T2 is placed inside a 6-way cross with two horizontal sides sealed with thin windows. Two NaI detectors are placed horizontally to T2 and perpendicular to the 90 degree beamline with their top facing to thin windows. The spectrum taken when the positron beam directed to the end of the 90 degree beamline with T2 in/out are shown in the Fig.~\ref{fig:in-out-runs}.
\begin{figure} \centering \begin{tabular}{cc}
{\scalebox{0.315} [0.315]{\includegraphics{5-Experiment/Figures/overlay/whole/NaI_L/r3737_sub_r3736.png}}} & {\scalebox{0.315} [0.315]{\includegraphics{5-Experiment/Figures/overlay/whole/NaI_R/r3737_sub_r3736.png}}} \\ (a) Original spectrum on left NaI. & (b) Original spectrum on right NaI.\\ & \\ & \\ {\scalebox{0.315} [0.315]{\includegraphics{5-Experiment/Figures/overlay/511_peak/NaI_L/r3737_sub_r3736.png}}} & {\scalebox{0.315} [0.315]{\includegraphics{5-Experiment/Figures/overlay/511_peak/NaI_R/r3737_sub_r3736.png}}} \\
(c) Spectrum with cut on left NaI. & (d) Spectrum with cut on right NaI.\\ & \\ \end{tabular} \caption{The time normalized spectrum of T2 in run (red) and T2 out run (blue). Top row shows original spectrum and bottom row shows incidents happened in 511~keV peak coincidently on both detectors.} \label{fig:in-out-runs} \end{figure}
Run No. 3735 (T2 in) and run No. 3736 (T2 out) are shown in the Fig.~\ref{fig:in-out-runs}. The positron counts are extracted by requiring events to happen coincidently in two detectors and in the 511~keV peak, subtracting the background from the signal ((T2~in) - (T2~out)), and finally integrating the 511~keV peak. On the bottom row in the Fig.~\ref{fig:in-out-runs}, the red peak is the background subtracted spectrum. The run parameters of run No. 3735 is given in the Table~\ref{tab:run3735}.
\begin{table} \centering \caption{Run Parameters of The Run No. 3735.} \begin{tabular}{lll} \toprule {Parameter} & {Unit} & {Value} \\ \midrule run number & & 3735 \\ repetition rate & Hz & 300 \\ run time & s & 1002 \\ pulses & & 301462 \\ events & & 9045 \\ e$^+$ Counts on NaI Detectors & & 256 $\pm$ 16\\ \bottomrule \end{tabular} \label{tab:run3735} \end{table}
% % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % %
\section{The Electron Beam Current Measurement}
When the electron beam is incident on T1, photons are generated by the bremsstrahlung processes. A photon scintillator was placed between Q9 and Q10 as shown in the Fig.~\ref{fig:Scint_e-} and was used as the electron beam monitor by measuring the photon flux generated by the electron beam. To calibrate the scintillator the electron beam was changed incrementally. The electron beam current was measured using FC1 (Faraday cup 1) and photon flux was measured using the photon scintillator. The electron current was observed with an oscilloscope and the photon flux is observed on a Analog to Digital Converter (ADC). As the electron beam current was decreased, the beam current observed on the oscilloscope decreased and the photon peak in the ADC shifted towards left end of the photon spectrum as shown in the Fig.~\ref{fig:ADC-CH9}. The measured results are shown in the Table~\ref{tab:scint_calb}. The relation between the electron beam current and scintillator ADC channel number is linear and the calibration factor is $(0.93 \pm 0.14)/50$ nVs/(ADC channel).
\begin{figure} \centering \includegraphics[scale=0.10]{5-Experiment/Hrrl_pos_jul2012_setup_Scint_e-_current.jpg} \caption{The electron beam monitor.} \label{fig:Scint_e-} \end{figure}
\begin{figure} \centering \includegraphics[scale=0.80]{5-Experiment/Figures/ScintilatorCalibration/EnDD1.eps} \caption{The photon flux detected using scintillator. The mean of the ADC channel decreased linearly as the electron beam current was decreased.} \label{fig:ADC-CH9} \end{figure}
\begin{table} \centering \caption{Scintillator Calibration Data.} \begin{tabular}{lll} \toprule {Run Number} & {Faraday Cup} & {Mean of ADC} \\ { } & {Charge Area (nVs)} & {Channel 9} \\ \midrule 3703 & $1201 \pm 10$ & $1126 \pm 0.8$ \\ 3705 & $777 \pm 110$ & $791.8 \pm 0.6$ \\ 3706 & $367.7 \pm 2.3$ & $242.1 \pm 0.3$ \\ \bottomrule \end{tabular} \label{tab:scint_calb} \end{table} The average electron beam charge in the experiment was calculated with two methods that both uses the ADC. The first method calculates the beam charge detected in each ADC bins and then sums up them all as given by \begin{equation} Q_{\text{e}^-} = \underset{i}{\sum} i \times (\text{bin~content}[i]) \times Q_{\text{Calb}} \times (\text{pulses/events}). \label{eq:q_calc1} \end{equation} \noindent In another method, the mean of the of the spectrum multiplied with total number of pulses in the run and calibrated to electron beam charge using calibration factor as given by \begin{equation} Q_{\text{e}^-} = (\text{Mean~ADC~Channel~Number}) \times (\text{pulses}) \times Q_{\text{Calb}}. \label{eq:q_calc2} \end{equation} The average results of the two methods is taken as the final electron beam charge. In run 3735, the electron beam charge is \begin{math} (4.8 \pm 0.5 ) \times 10^{-3}\end{math}~C. The error on electron beam charge is obtained by propagating the error on the calibration factor and finding the variance of two methods.
%For example, the charge in run 3735 is calculated with method 1 and 2 are given in Eq.~\ref{eq:q_calc1_reslut} and ~\ref{eq:q_calc2_reslut}. %\begin{equation} %\begin{align*} %Q_{e^-} & = \underset{i}{\sum} i \times (bin~counts[i]) \times (856.9 \pm 1.0)(ADC~channel) \times (301462/9045)\\ %& = (4.8 \pm 0.7 ) \times 10^{-3}~C. %\end{align*} %\label{eq:q_calc1_reslut} %\end{equation} %\begin{equation} %\begin{align*} %Q_{e^-} &= (856.9 \pm 1.0)(ADC~channel) \times 301462 \times (0.93 \pm 0.14)/50 (nVs/(ADC~channel))\\ %&= (4.8 \pm 0.7 ) \times 10^{-3}~C. %\end{align*} %\label{eq:q_calc2_reslut} %\end{equation}
\section{Positron Rate Estimation}
The signals from NaI detectors were sent to the ADC. The spectrum is shown in the Fig.~\ref{fig:pos_NaILR} are the background subtracted spectrum obtained by subtracting the counts when T2 is out from the counts when T2 is in. The (a) and (b) are the spectrum of all events. The (c) and (d) are the spectrum of events coincident on both detectors, in the 511~keV peak, and after background subtraction. \begin{figure} \centering \begin{tabular}{cc} {\scalebox{0.8} [0.80]{\includegraphics[scale=0.40]{5-Experiment/Figures/subtract/whole/NaI_L/r3735_sub_r3736.png}}} & {\scalebox{0.8} [0.80]{\includegraphics[scale=0.40]{5-Experiment/Figures/subtract/whole/NaI_R/r3735_sub_r3736.png}}} \\ (a) & (b) \\ & \\ & \\ {\scalebox{0.8} [0.8]{\includegraphics[scale=0.40]{5-Experiment/Figures/subtract/511_peak/NaI_L/r3735_sub_r3736.png}}} & {\scalebox{0.8} [0.8]{\includegraphics[scale=0.40]{5-Experiment/Figures/subtract/511_peak/NaI_R/r3735_sub_r3736.png}}} \\ (c) & (d) \\
& \\
\end{tabular} \caption{Photon spectrum after background subtraction. (a) and (b) are spectrum of left and right NaI detector after background subtractions. (c) and (d) are the spectrum of left and right NaI detector after background subtractions and requiring the event to happen coincidently in both detectors in their 511~keV peak. } \label{fig:pos_NaILR} \end{figure}
To find errors on the positron beam energy at different energies, the electron beam is directed to the phosphorous screen at the end of the 90 degree beamline. The positron beam current is too low to be observed on the screen and the electron beam was used to instead. The beam centered and then steered from the center to the edge of the screen by changing the current by $\Delta$I = 0.1~A. This 0.1~A change in the dipole current corresponding to 0.06 MeV difference in the beam energy for 3~MeV beam. For other energies, the errors are also 0.06~MeV after rounding up.
\section{Positron to Electron Ratio} The measured ratio of positron to electron is given the Table~\ref{tab:e+2e-} and the Fig.~\ref{fig:e+2e-}. The errors on the positron counts are statistical errors. The errors of the positrons to electrons ratios are obtained by propagating the errors of both electron and positron rates. %error on total counts = sqt(total counts). Rate = Counts/time. Error on rates = sqrt(d(rate)/d(counts)^2*(error on the counts)^2)=sqrt((error on the counts)^2/time^2)=sqrt(counts/time^2)=sqrt(rate/time). \begin{table} \centering \caption{Positron to Electron Rate Ratio.} \begin{tabular}{lc} \toprule {Energy} & {Positron to Electron Ratio} \\ \midrule $1.02 \pm 0.06$ & $(0.19 \pm 0.19)\times10^{-16}$ \\ $2.15 \pm 0.06$ & $(0.69 \pm 0.24)\times10^{-16}$ \\ $3.00 \pm 0.06$ & $(8.25 \pm 0.96)\times10^{-15}$ \\ $4.02 \pm 0.06$ & $(4.20 \pm 0.80)\times10^{-15}$ \\ $5.00 \pm 0.06$ & $(0.62 \pm 0.16)\times10^{-16}$ \\
\bottomrule \end{tabular} \label{tab:e+2e-} \end{table} \begin{figure} \centering \includegraphics[scale=0.72]{5-Experiment/Figures/Ratio/R.eps} \caption{The Ratio of the positrons detected to the electrons in experiment.} \label{fig:e+2e-} \end{figure}
%\subsubsection{Error on Ratio} % %Error on electron beam is derived from: % %Error on positron beam rate is derived from: $\sqrt{\frac{positron~rate}{run~time}}$ % %\subsubsection{Annihilation Target Angle} %Use simulation to determine how sensitive annihilation of positrons is to angle. % %What is the dependence of the annihilation target angle with the probability of a positron annihilating in the target and producing a photon that is detected by the NaI detector, % %What is the distribution of 511s as a function of angle phi when theta is 90 degrees? Are they uniformly produced? %\subsubsection{Energy cut systematics} % %How does the positron production efficiency change when you change the range of the 511 cut.
Conclusions and Suggestions
\chapter{Conclusions and Suggestions}
The HRRL cavity was moved to current location. New magnetic elements and diagnostic tolls were added to the beamline. The new HRRL beamline was successfully reconfigured to produce positrons while still can transport electrons to the experimental cell.
An OTR based diagnostic tool was developed and used to measure the beam emittance of the HRRL. The electron beam profile was not described well using a single Gaussian distribution but rather by a super Gaussian or Lorentzian distribution. The projected emittance of the HRRL was measured to be less than 0.4~$\mu$m as measured by the OTR based tool described above when accelerating electrons to an energy of 15~MeV.
Successfully constructed a positron detection system using two NaI detectors and the thin tungsten target placed in the 6-way cross. Successfully measured positrons at different energies (1 $-$ 5~MeV) in experiment. The ratio of positrons being detected on NaI detectors to electrons incident on T2 is on the order of $10^{-15}$ and the peak is observed around 3~MeV. %In the experiment, quadrapoles were optimized to only transport 2~MeV and due to the limited beam time and it could have diminished transportation efficiency for other energies. %Further experimental study is necessary to investigate the positron beam energy distribution.
Simulation results indicate that the transportation efficiency varies for different energies. Higher energies has better transportation efficiency. While simulation results agree with experiment in that the peak energy distribution is around 3~MeV, it predicts higher positron to electron ratio as shown in the Fig~\ref{fig:e+2e-exp-sim}. %Beam loss
Experimental results show quadrupole magnets are not efficient in collecting positrons, since positrons have large angular distribution. Solenoid might be better option to improve the collection efficiency of the positrons. Placing the solenoid close the production target would increase the positron transportation efficiency since it can capture more positrons. %7. Experimental results show quadrupole magnets are not efficient in collecting positrons, since positrons have large angular distribution. Solenoid might be able to improve the collection efficiency of positrons~\cite{kim-bindu-solenoid} and should be placed as close the production target as possible for better efficiency.
\begin{figure} \centering \includegraphics[scale=0.80]{6-Conclusion/Figures/Overlay_Exp-Sim-Ratio/R1.eps} \caption{Ratio of positrons detected to electrons in experiment and simulation.} \label{fig:e+2e-exp-sim} \end{figure}
List of Figures
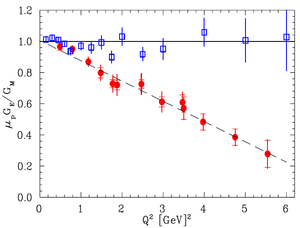 1.1 Form factor ratio, obtained by Rosenbluth Technique (hollow square) and results from Recoil Polarization Technique [5]. . . . . 3
1.1 Form factor ratio, obtained by Rosenbluth Technique (hollow square) and results from Recoil Polarization Technique [5]. . . . . 3
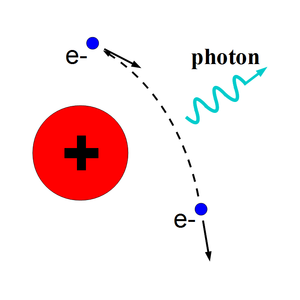 1.2 Photon generation from Bremsstrahlung processes. . . . . . . . . . . . . . . 4
1.2 Photon generation from Bremsstrahlung processes. . . . . . . . . . . . . . . 4
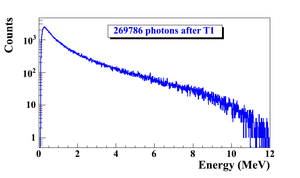 1.3 Simulated Bremsstrahlung photon energy right after a tungsten foil. . . . . . 5
1.3 Simulated Bremsstrahlung photon energy right after a tungsten foil. . . . . . 5
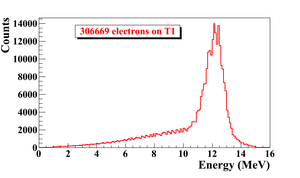 1.4 Simulated electron energy distribution right before a tungsten foil. . . . . . . 6
1.4 Simulated electron energy distribution right before a tungsten foil. . . . . . . 6
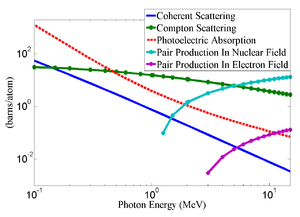 1.5 Cross section for each type of photon interaction with tungsten as function of photon energy [10]. . . . . . . . . . . . . . . . 6
1.5 Cross section for each type of photon interaction with tungsten as function of photon energy [10]. . . . . . . . . . . . . . . . 6
 1.6 Pair production. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.6 Pair production. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
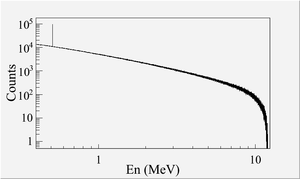 1.7 Photon spectrum of 12 MeV mono energy 10 million electrons impinge on a 1.016 mm thick tungsten target. . . . . . . . . . . 8
1.7 Photon spectrum of 12 MeV mono energy 10 million electrons impinge on a 1.016 mm thick tungsten target. . . . . . . . . . . 8
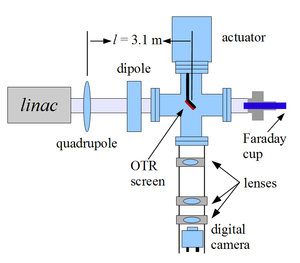 1.8 Apparatus used to measure the beam emittance. . . . . . . . . . . . . . . . . 11
1.8 Apparatus used to measure the beam emittance. . . . . . . . . . . . . . . . . 11
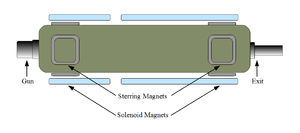 2.1 HRRL cavity. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.1 HRRL cavity. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
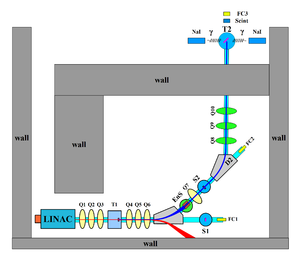 2.2 HRRL beamline layout and parts. . . . . . . . . . . . . . . . . . . . . . . . . 17
2.2 HRRL beamline layout and parts. . . . . . . . . . . . . . . . . . . . . . . . . 17
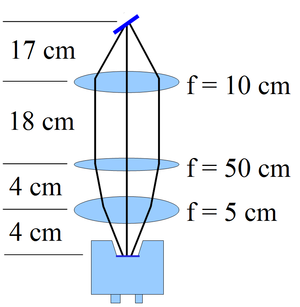
 2.3 The OTR Imaging system. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.3 The OTR Imaging system. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
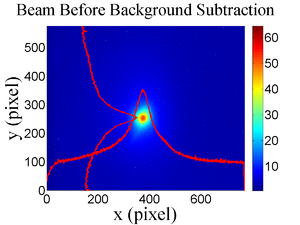
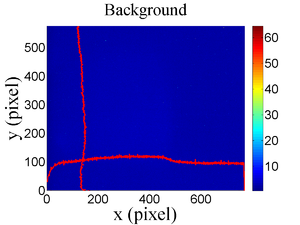
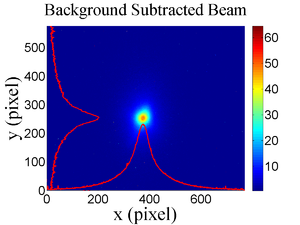 2.4 Background subtracted to minimize impact of dark current; (a) a beam with the dark current and background noise, (b) a background image, (c) a beam
image when dark background was subtracted. . . . . . . . . . . . . . . . . . 21
2.4 Background subtracted to minimize impact of dark current; (a) a beam with the dark current and background noise, (b) a background image, (c) a beam
image when dark background was subtracted. . . . . . . . . . . . . . . . . . 21
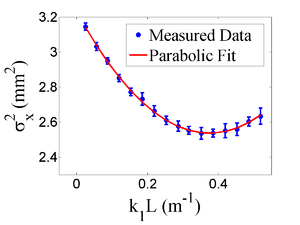
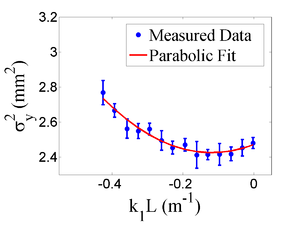 2.5 Square of rms values and parabolic fittings. . . . . . . . . . . . . . . . . . . . 23
2.5 Square of rms values and parabolic fittings. . . . . . . . . . . . . . . . . . . . 23
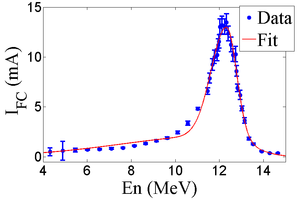 2.6 HRRL energy scan (blue dots) and fit (red line) with two skewed Gaussian distribution. . . . . . . . . . . . . . . 25
2.6 HRRL energy scan (blue dots) and fit (red line) with two skewed Gaussian distribution. . . . . . . . . . . . . . . 25
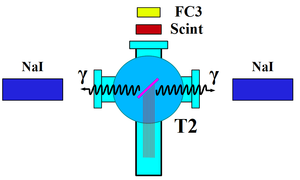 2.7 Positron Detection System. T2 (pink) is 45 degree placed with horizontal plane, then rotated towards left detector 45 degree. . . . . . . . . . . 26
2.7 Positron Detection System. T2 (pink) is 45 degree placed with horizontal plane, then rotated towards left detector 45 degree. . . . . . . . . . . 26
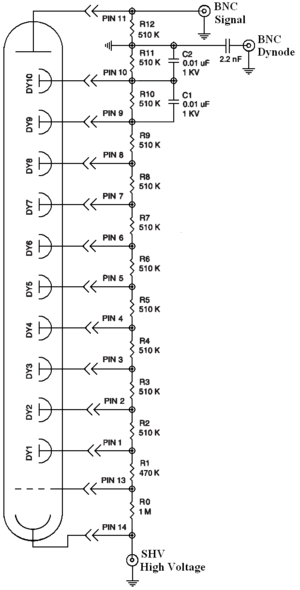 2.8 Modified PMT base design. . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.8 Modified PMT base design. . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
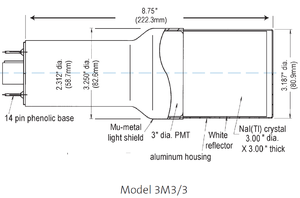 2.9 NaI crystal dimension. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.9 NaI crystal dimension. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
 2.10 NaI crystals and new bases. . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.10 NaI crystals and new bases. . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
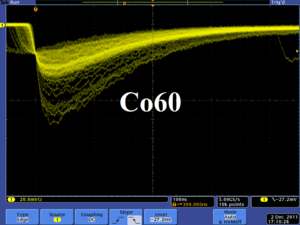 2.11 Pulses from Co-60 source observed on the scope. The amplitude is about 60 mV. The rise time is larger than 50 ns, and the fall time is larger than 700 ns. . . . . . . . .. . . . . . . . . 30
2.11 Pulses from Co-60 source observed on the scope. The amplitude is about 60 mV. The rise time is larger than 50 ns, and the fall time is larger than 700 ns. . . . . . . . .. . . . . . . . . 30
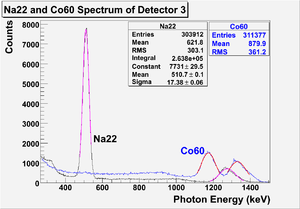 2.12 Calibrated NaI spectrum of Na-22 and Co-60 sources. . . . . . . . . . . . . . 30
2.12 Calibrated NaI spectrum of Na-22 and Co-60 sources. . . . . . . . . . . . . . 30
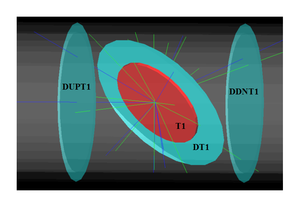 3.1 T1 is positron production target with same geometry and material as real target. DUPT1 is virtual detector located upstream to sample incoming electron
beam. DDNT1 is down stream virtual detector; DT1 is a virtual detector that is placed right after T1 with same angle as T1. . . . . . . . . 34
3.1 T1 is positron production target with same geometry and material as real target. DUPT1 is virtual detector located upstream to sample incoming electron
beam. DDNT1 is down stream virtual detector; DT1 is a virtual detector that is placed right after T1 with same angle as T1. . . . . . . . . 34
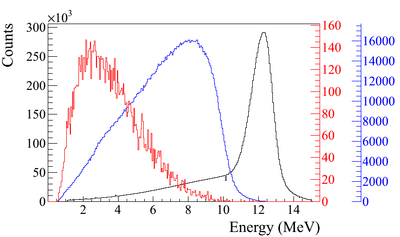 3.2 Energy distribution of positrons detected on virtual detector DDNT1. . . . . 35
3.2 Energy distribution of positrons detected on virtual detector DDNT1. . . . . 35
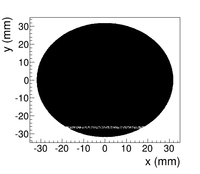
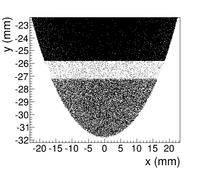 3.3 Transverse spacial and angular distribution of positrons on the virtual detector DDNT1. . . . . . . . . . 36
3.3 Transverse spacial and angular distribution of positrons on the virtual detector DDNT1. . . . . . . . . . 36
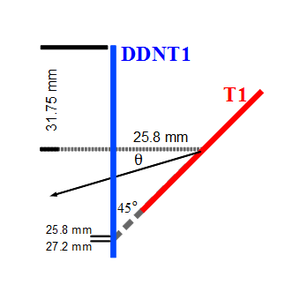 3.4 Geometry of the target T1 and the virtual detector DDNT1. . . . . . . . . . 37
3.4 Geometry of the target T1 and the virtual detector DDNT1. . . . . . . . . . 37
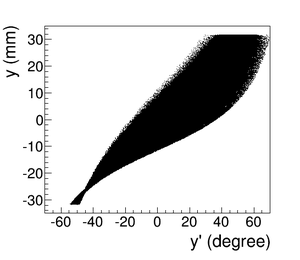
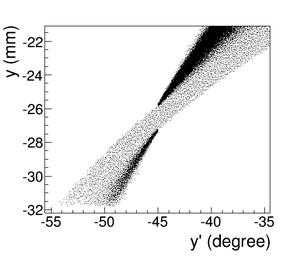 3.5 Positron beam distribution Y divergence vs. Y spacial distribution on DDNT1. 37
3.5 Positron beam distribution Y divergence vs. Y spacial distribution on DDNT1. 37
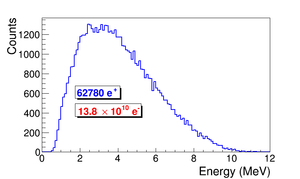 300 px
3.6 Positron beam energy distribution detected on the downstream of T2. . . . . 38
300 px
3.6 Positron beam energy distribution detected on the downstream of T2. . . . . 38
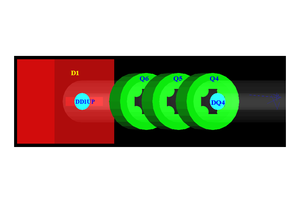 3.7 Step 2 setup. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.7 Step 2 setup. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
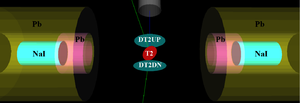 3.8 T2 and virtual detectors located upstream (DT2UP) and downstream (DT2DN) of T2. NaI dettectos and Pb shielding. . . . . . . . . . . 40
3.8 T2 and virtual detectors located upstream (DT2UP) and downstream (DT2DN) of T2. NaI dettectos and Pb shielding. . . . . . . . . . . 40
 3.9 NaI detector eficiency [21]. . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.9 NaI detector eficiency [21]. . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
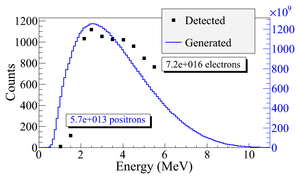 3.10 Positrons generated detected on virtual detector DDNT1 and 511 keV counts
detected by NaI detectors in coincidence mode (100 % eficiency assumed). . 42
3.10 Positrons generated detected on virtual detector DDNT1 and 511 keV counts
detected by NaI detectors in coincidence mode (100 % eficiency assumed). . 42
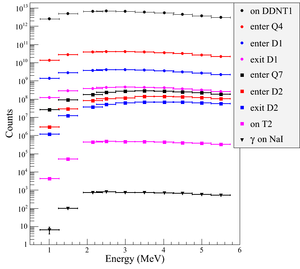 3.11 Predicted number positrons of transported. Black circle: positrons after T1. Red circle: positrons enter Q4. Blue circle: positrons enters D1. Magenta
circle: positrons reaches T2. . . . . . . . . . . . . . . .. . . 42
3.11 Predicted number positrons of transported. Black circle: positrons after T1. Red circle: positrons enter Q4. Blue circle: positrons enters D1. Magenta
circle: positrons reaches T2. . . . . . . . . . . . . . . .. . . 42
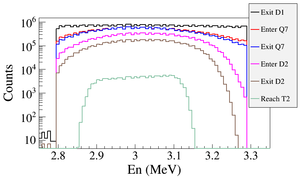 3.12 Beam transported when dipoles are set for 3 MeV positrons. . . . . . . . . . 45
3.12 Beam transported when dipoles are set for 3 MeV positrons. . . . . . . . . . 45
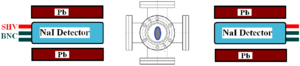 4.1 Positron detection using T2 and NaI detectors. . . . . . . . . . . . . . . . . . 49
4.1 Positron detection using T2 and NaI detectors. . . . . . . . . . . . . . . . . . 49
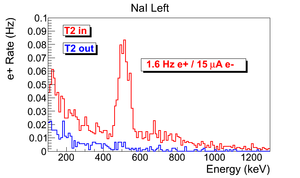
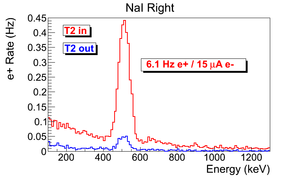
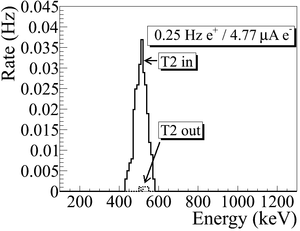
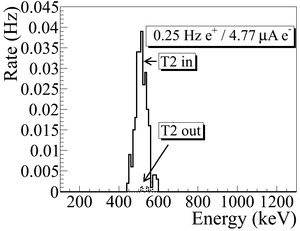 4.2 T2 in run (red) and T2 out background run (blue) time normalized spectrum. Top row shows original spectrum and bottom row shows incidents only happen
in 511 keV peak coincidently on both detectors. . . . . . . . . . . . 50
4.2 T2 in run (red) and T2 out background run (blue) time normalized spectrum. Top row shows original spectrum and bottom row shows incidents only happen
in 511 keV peak coincidently on both detectors. . . . . . . . . . . . 50
 4.3 Electron beam monitor. . . . . . . . . . . . . . . . . .. . . . 52
4.3 Electron beam monitor. . . . . . . . . . . . . . . . . .. . . . 52
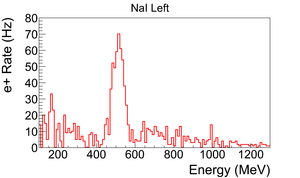
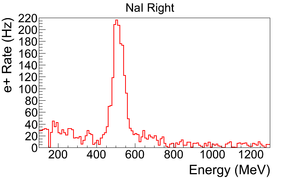
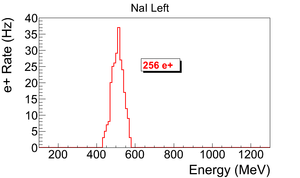
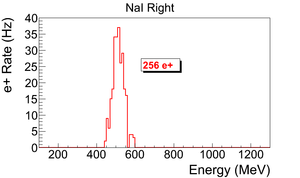 4.4 Electron beam monitor ADC signal . . . . . . . . . . . . . . . . . . . . . . . 52
4.4 Electron beam monitor ADC signal . . . . . . . . . . . . . . . . . . . . . . . 52
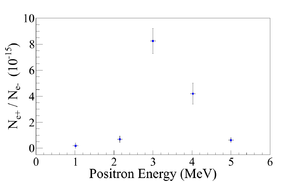 4.5 Ratio of positrons detected to electrons in experiment. . . . . . . . . . . . . 55
4.5 Ratio of positrons detected to electrons in experiment. . . . . . . . . . . . . 55
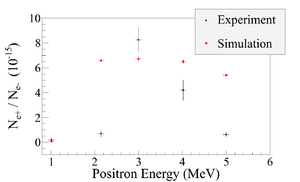 5.1 Ratio of positrons detected to electrons in experiment and simulation. . . . . 58
5.1 Ratio of positrons detected to electrons in experiment and simulation. . . . . 58