Sadiq Thesis

Introduction

Positron

Positron is the antimatter of electron. Positrons have same mass as electron ( [math]511~\frac{keV}{c^2}[/math]), carries positive charge, and it is noted as "[math]e^+[/math]".

Positrons predicted by Paul Dirac in 1928, <ref name="Dirac1928"> The Quantum Theory of the Electron, P. A. M. Dirac, Proc. R. Soc. Lond. A February 1, 1928 117 778 610-624;</ref>, and experimentally observed by Dmitri Skobeltsyn in 1929 and by Carl D. Anderson in 1932 <ref name="e+_discover"> General Chemistry, Taylor and Francis. p. 660. </ref>. Anderson also coined the term positron and he won the Nobel Prize for Physics in 1936.

<ref name="name"> BOOK_Gernal, Auther, Month_Year,issue,page </ref>

Apparatus

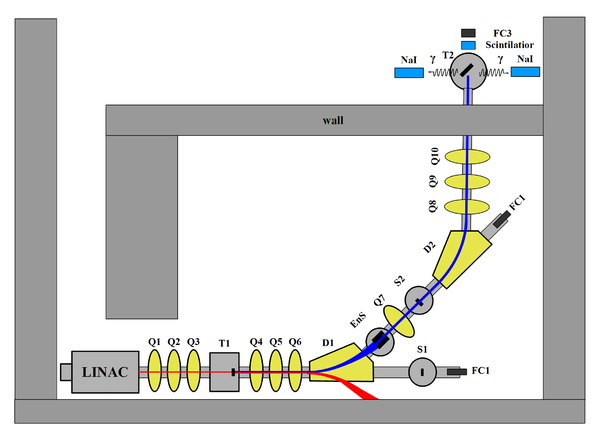
HRRL Positron Beamline

HRRL beamline layout is given in the figure below, and the item descriptions are given in the table below.

HRRL beamline layout.

Item	Description
T1	Positron target
T2	Annihilation target
EnS	Energy Slit
FC1, FC2	Faraday Cups
Q1,...Q10	Quadrupoles
D1, D2	Dipoles
NaI	NaI Detecotrs
OTR	Optical Transition Radiaiton screen
YAG	Yttrium Aluminium Garnet screen

Som parameters of HRRL is given by:

Parameter	Unit	Value
maximum energy	MeV	16
peak current	mA	100
repetition rate	Hz	300
absolute energy spread	MeV	2-4
macro pulse length	ns	>50

Beam properties

Emittance Measurement

Emittance is an important parameter in accelerator physics. If emittance with twiss parameters are given at the exit of the gun, we will be able to calculate beam size and divergence any point after the exit of the gun. Knowing the beam size and beam divergence on the positron target will greatly help us study the process of creating positron. Emittance with twiss parameters are also key parameters for any accelerator simulations. Also, energy and energy spread of the beam will be measured in the emittance measurement.

What is Emittance

Fig.1 Phase space ellipse <ref name="MConte08"></ref>.

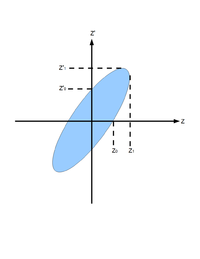
In accelerator physics, Cartesian coordinate system was used to describe motion of the accelerated particles. Usually the z-axis of Cartesian coordinate system is set to be along the electron beam line as longitudinal beam direction. X-axis is set to be horizontal and perpendicular to the longitudinal direction, as one of the transverse beam direction. Y-axis is set to be vertical and perpendicular to the longitudinal direction, as another transverse beam direction.

For the convenience of representation, we use [math]z[/math] to represent our transverse coordinates, while discussing emittance. And we would like to express longitudinal beam direction with [math]s[/math]. Our transverse beam profile changes along the beam line, it makes [math]z[/math] is function of [math]s[/math], [math]z~(s)[/math]. The angle of a accelerated charge regarding the designed orbit can be defined as:

[math]z'=\frac{dz}{ds}[/math]

If we plot [math]z[/math] vs. [math]z'[/math], we will get an ellipse. The area of the ellipse is an invariant, which is called Courant-Snyder invariant. The transverse emittance [math]\epsilon[/math] of the beam is defined to be the area of the ellipse, which contains 90% of the particles <ref name="MConte08"> M. Conte and W. W. MacKay, “An Introduction To The Physics Of Particle Accelera tors”, World Scientifc, Singapore, 2008, 2nd Edition, pp. 257-330. </ref>.

By changing quadrupole magnetic field strength [math]k[/math], we can change beam sizes [math]\sigma_{x,y}[/math] on the screen. We make projection to the x, y axes, then fit them with Gaussian fittings to extract rms beam sizes, then plot vs [math]\sigma_{x,y}[/math] vs [math]k_{1}L[/math]. By Fitting a parabola we can find constants [math]A[/math],[math]B[/math], and [math]C[/math], and get emittances.

Emittance Measurements with an OTR

A beam emittance measurement of the HRRL was performed at Idaho State University's IAC with YAG (Yttrium Aluminium Garnet) was performed. Due to the high sensitivity of YAG, the beam image was saturated and beam spot pears rather big. Comparison study shows that for same beam YAG screen shows bigger beam size than Optical Transition Radiation (OTR) screen. An OTR based viewer was installed to allow measurements at the high electron currents available using the HRRL.

The OTR screen is 10 [math]\mu m[/math] thick aluminium. Beam images were taken with digital CCD camera, a MATLAB tool were used to extract beamsize and emittance.

The visible light from the OTR based viewer is produced when a relativistic electron beam crosses the boundary of two mediums with different dielectric constants. Visible radiation is emitted at an angle of 90 degree with respect to the incident beam direction<ref name="OTR"> Tech. Rep., B. Gitter, Los Angeles, USA (1992). </ref> when the electron beam intersects the OTR target at a 45 degree angle. These backward-emitted photons are observed using a digital camera and can be used to measure the shape and intensity of the electron beam based on the OTR distribution.

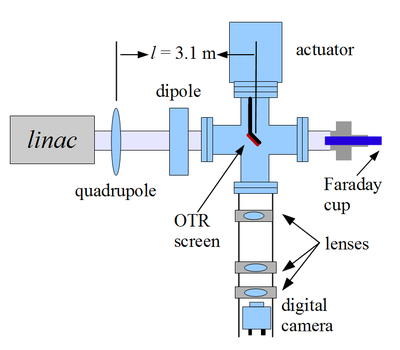
Quadrupole Scanning Method

Fig. Simplified setup configuration for HRRL beamline at 2011 March measurement.

Figure on the right illustrates the apparatus used to measure the emittance using the quadrupole scanning method. A quadrupole is positioned at the exit of the linac to focus/de-focus the beam as observed on a downstream view screen. The 3.1~m distance between the quadrupole and the screen was chosen in order to minimize chromatic effects and to satisfy the thin lens approximation.

Experimental setup is shown in the following figure

I chose one of the quad at a time to do the scan and turned off all the other quads. Optical transition radiation was observed at OTR target. At the end of 0 degree beamline I had a Faraday cup to measure the charge of the beam. Camera cage system was located below the OTR target. There are 3 lenses used to focus lights from target to the CCD camera. Target can be pushed into or taken out of the beamline by the actuator at the top.

OTR Target can be pushed into or taken out of the beamline vertically by the actuator at the top, which is attached to the 6-way cross. This actuator controlled remotely at the control desk.

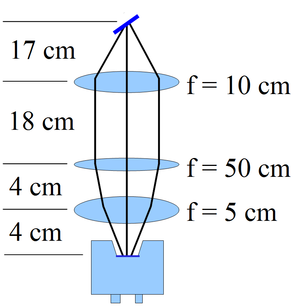
Camera cage system was located below the OTR target. Cage system attached to the bottom of the 6-way cross. Lower end of cross is a transparent window. There are 3 lenses used to focus lights from target to the CCD camera. They have focal length of 100 mm, 500 mm, and 50 mm.

The lens closest to the OTR target is 10 cm away from the target, an it has 100 mm focal length. This lens was located as close to the target as possible, so that we might collect as much OTR light as possible, and it was thus called collector lens. The lens in the middle has focal length of 500 mm. Moving this lens will change total focal length in a small amount, and this allow us to do fine tuning. Thus, we called this lens fine tuning lens. The last lens, which is furthest from target, and closed to the CCD camera has the shortest focal length of 5o mm. Its short focal length allow us to focus the light on the very small sensing area of the CCD camera.

Fig. HRRL beamline: Optical lenses lay out for optical cage system.

Experiment with OTR

Optical Transition Radiation (OTR): Transition radiation is emitted when a charge moving at a constant velocity cross a boundary between two materials with different dielectric constant.

When relativistic electron beam pass through Aluminum target OTR is produced. OTR are taken for different quadrupole coil currents.

Fig. OTR image of 0 Amp Q1 coil current.

Fig. OTR image of +1 Amp Q1 coil current.

Fig. OTR image of +2 Amp Q1 coil current.

Data Analysis and Results

The projection of the beam is not Gaussian distribution. So, I fit Super Gaussian fitting <ref name="BeamDisBeyondRMS"> F.-J Decker, “Beam Distributions Beyond RMS”, BIW94, Vancouver,CA,Sep 1994, . </ref>.

I used the MATLAB to analyze the data. The results shows that:

[math] \sigma_x^2= (3.678 \pm 0.022) + (-4.17 \pm 0.22)k_1L + (5.55 \pm 0.42)(k_1L)^2 [/math]

[math] \epsilon_x = 0.417 \pm 0.023~mm*mrad ~\Rightarrow~ \epsilon_{n,x} = 11.43 \pm 0.64~mm*mrad[/math]

[math] \beta_x=1.385 \pm 0.065, \alpha_x=0.97 \pm 0.07 [/math]

[math]\sigma_y^2 = (2.843 \pm 0.044) + (1.02 \pm 0.52)k_1L + (3.8 \pm 1.2)(k_1L)^2 [/math]

[math] \epsilon_y = 0.338 \pm 0.065~mm*mrad ~\Rightarrow~ \epsilon_{n,y} = 9.3 \pm 1.8~mm*mrad[/math]

[math] \beta_y=1.17 \pm 0.19, \alpha_y=0.22 \pm 0.10 [/math]

Data Analysis

Signal extraction

For 3 MeV and on detector show all the steps

1. Raw counts target in and out (calibrated energy)
2. Normalized counts
3. background subtracted
4. Integral (zoomed in and with error)

Example of error propagation for the above

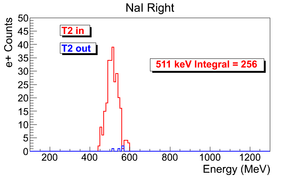
Raw counts target in and out

The ingeral shown in read is from the background is subtracted spectrum.

run in

run out

NaI Left: image with cut

NaI Right: image with cut

3735

3736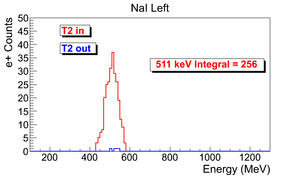

Reprate = 300 Hz

Run time = 1002 s

Pulses = 301462

Events = 9045 (Hz)

e+ rate NaI Left = 256 +- 16 (Hz).

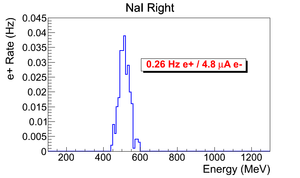
Normalized counts

This a normalized spectrum (no background subtraction).

run in

run out

NaI Left: image with cut

NaI Right: image with cut

3735

3736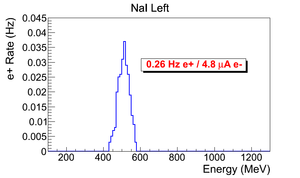

3735 and 3736

Reprate = 300 Hz

Run time = 1002 s

Pulses = 301462

Events = 9045

Total number of electrons in this run = 2.98568e+016 +- 4.49846e+015

Total charge of electrons in this run = 0.00478358 +- 0.000720733 C

e- rate = 2.97972e+013 +- 4.48948e+012 (Hz)

e- current:I_e- =4.77403e-006+-7.19295e-007 (A).

e+ rate = 0.259481 +- 0.0160923 (Hz).

Ne+/Ne-=8.70825e-015+-1.41886e-015.

Ne+/I_e-=0.25948 Hz e+ / 4.774 [math]\mu[/math]A e-

hand calculation of error

[math]R = \frac{N_{e^+}}{N_{e^-}} = \frac{ 0.259 \pm 0.016 Hz}{ (2.98 \pm 0.45) \times 10^{13} Hz} = 0.087 \times 10^{-13} = 8.69 \times 10^{-15}[/math]

[math]\Delta R = \sqrt{\frac { \Delta N_{e^+}^2 }{ N_{e^-}^{2} } + (- \frac{ N_{e^+} }{ N_{e^-}^{2} })^2 \Delta N_{e^-}^{2} } = \frac{\sqrt{ \Delta N_{e^+}^{2} + \frac{ N_{e^+}^{2} }{ N_{e^-}^{2} } \Delta N_{e^-}^{2} }}{ N_{e^-}}[/math] = \frac{\sqrt{ \Delta N_{e^+}^{2} + \frac{ N_{e^+}^{2} }{ N_{e^-}^{2} } \Delta N_{e^-}^{2} }}{ N_{e^-}}</math>

[math]\Delta R = \frac{\sqrt{ 0.016^{2} + (\frac{ 0.25 }{ 3.909\times 10^{13} } 0.225 \times 10^{13})^{2} }}{ 3.909\times 10^{13}} = \frac{\sqrt{ 0.000256 + 0.000207 }}{ 3.909\times 10^{13}} = \frac{\sqrt{ 0.000463 }}{ 3.909\times 10^{13}} = \frac{0.0215}{ 3.909\times 10^{13}} = 0.0055 \times 10^{-13} = 5.5 \times 10^{-16}[/math]

References

<references/>