Difference between revisions of "2-Neutron Correlation"
Jump to navigation
Jump to search
| Line 41: | Line 41: | ||
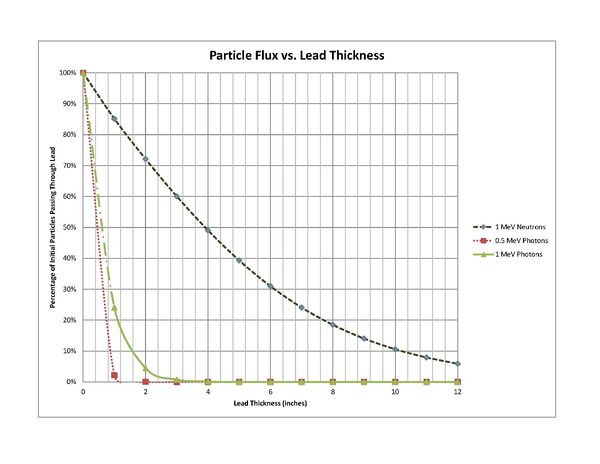
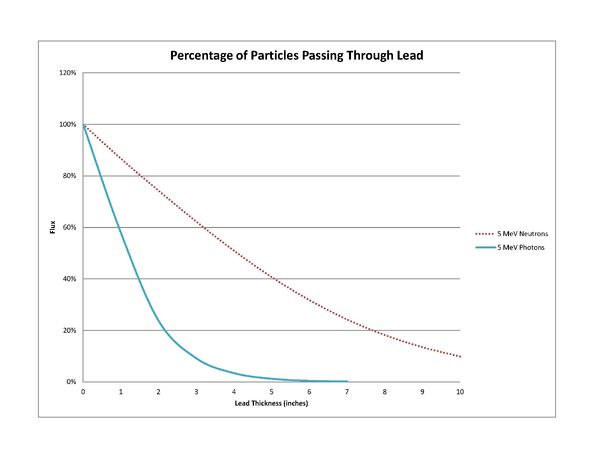
Using MCNPX, a simulation was done to determine how much of the neutrons and photons from the target will be blocked by various thickness of lead. With a monochromatic pencil beam of incident particles, the following results illustrate how much of the initial beam actually made it through the lead. | Using MCNPX, a simulation was done to determine how much of the neutrons and photons from the target will be blocked by various thickness of lead. With a monochromatic pencil beam of incident particles, the following results illustrate how much of the initial beam actually made it through the lead. | ||
| − | [[File:1MeV_Lead.jpg | | + | [[File:1MeV_Lead.jpg | 600px]] |
| − | [[File:5MeV_Lead.jpg | | + | [[File:5MeV_Lead.jpg | 600px]] |
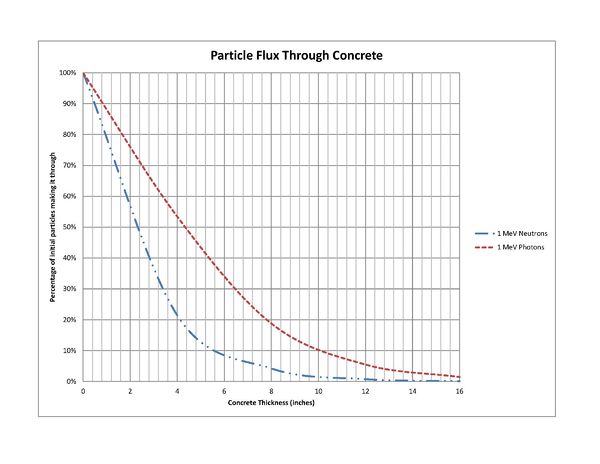
==Neutron and Photon Flux Through Concrete== | ==Neutron and Photon Flux Through Concrete== | ||
| − | [[File:1MeV_Concrete.jpg | | + | [[File:1MeV_Concrete.jpg | 600px]] |
[https://wiki.iac.isu.edu/index.php/User:Jasenswanson Go Back] | [https://wiki.iac.isu.edu/index.php/User:Jasenswanson Go Back] | ||
Revision as of 18:32, 8 June 2012
Big Detector Solid Angle Calculations
- MCNPX Simulation
- 14 MeV neutron source, emitted isotropically ()
- Detector placed 1m away from source
- face of the detector is 15.24cm x 76.2cm, and 3.6cm deep
The solid angle can be found from the number of particles hitting the detector as:
- Results
- Out of 1E9 neutrons generated, 8618287 neutrons hit the detector
-
- if the detector is placed 70cm away from the source,
- if the detector is placed 65cm away from the source,
-
- As a test to verify our results
- We change the detector size to 2cm by 2cm and used 1E9 neutrons again
- 32061 neutrons struck the detector
- And, as a second test to verify our results
- We change the detector size to 1cm by 1cm and used 1E9 neutrons again
- 7965 neutrons struck the detector
- Now, what neutron singles rate into the detector should correspond to 1 fission per pulse?
- If we have 1 fission per pulse and each fission emits on average 2.3 neutrons, we should expect 2.3 neutrons/pulse
- The number of neutrons hitting the detector per pulse is found as
- @ 1 meter => 0.0198 neutrons hitting the detector per pulse
- @ 70 cm => 0.0379 neutrons hitting the detector per pulse
- Taking into account the efficiency of the detector , the number detected per pulse can be found as
- @ 1 meter from source => () neutrons detected per pulse
- @ 70 cm from source => () neutrons detected per pulse
Neutron and Photon Flux Through Lead
Using MCNPX, a simulation was done to determine how much of the neutrons and photons from the target will be blocked by various thickness of lead. With a monochromatic pencil beam of incident particles, the following results illustrate how much of the initial beam actually made it through the lead.