Difference between revisions of "HRRL 03-18-2011"
(→Q1) |
|||
| Line 427: | Line 427: | ||
Did not reach minimum. | Did not reach minimum. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[HRRL_Emittance_Measurements_March14-18-2011]] | ||
Revision as of 04:09, 10 May 2011
Tune parameters
Previous Tune at the higher energy
| Solenoid 1 | 5.4 A |
| Solenoid 2 | 5.5 A |
| Gun Ver | -0.2 A |
| Gun Hor | +0.4 A |
| Output Hor | -0.5 A |
| Output Ver | -0.5 A |
| Gun HV | +9.75 (Knob Setting) |
| Gun Grid Voltage | 5.25 (Knob Setting) |
| RF frequency | 2855.813 MHz |
| Modulator HV Power Supply | 4.11 (Knob Setting) |
| RF macro Pulse Length (FWHM) | 200 ns |
Solenoid comparison with yesterdays higher energy tune
Quad Scans
To test reproducibility from yesterday. Scan at 40, 20, 10, 5 mA peak currents. Scan twice on each Current.
Do Energy Scan
Bend the beam through 45 bending dipole, take images on the scope of FC and YAG images.
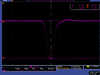
| D1 current | Energy | FC peak Volt | Pic |
| (A) | MeV | mV | |
| 28 | 11.85 | 39 | 
|
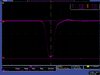
| 29 | 12.3 | 74 | 
|
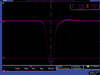
| 30 | 12.74 | 93 | 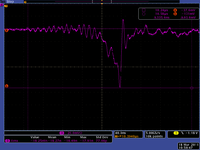
|
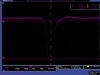
| 30.5 | 12.96 | 65 | 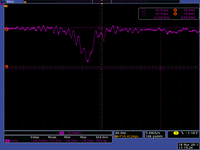
|
| 30.7 | large uncertainty | 22 | 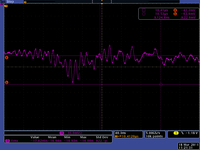
|
Quad 1 Scan
| Quad 1 | OTR Pict | FC pict |
| (A) | ||
| +0 |  |

|
| +0.2 |  |

|
| +0.4 |  |

|
| +0.6 |  |

|
| +0.8 |  |

|
| +1.0 |  |

|
| +1.2 |  |

|
| +1.4 |  |

|
| +1.6 |  |

|
| +1.8 |  |

|
| +2.0 |  |
|
Scan Quad 4
Calibration
Estimate the error in the above calibration
| cal_h (mm/px) | cal_v (mm/px) | |
| 0.04308 | 0.04228 | |
| 0.04302 | 0.04196 | |
| 0.04320 | 0.04220 | |
| 0.04320 | 0.04189 | |
| 0.04239 | 0.04165 | |
| 0.04337 | 0.04189 | |
| 0.04320 | 0.04220 | |
| mean (mm/px) | mean (mm/px) | |
Data Analysis
Preliminary results
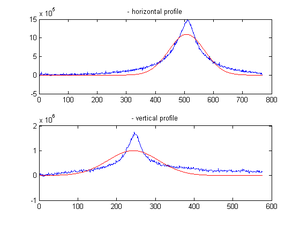
Here is the study on how to fit non_Gaussian curve. I fitted for whole image as well as parts of the image.
Here is beam profile, which is non-Gaussian.
Fits for whole image:
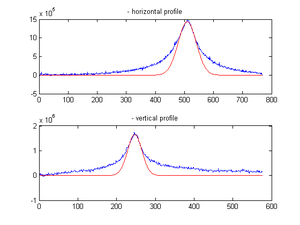
Fits for x=[362,404] and y=[241,301]:
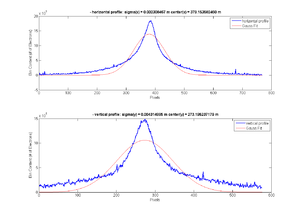
Gaussian fitted for whole image
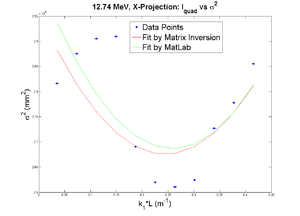
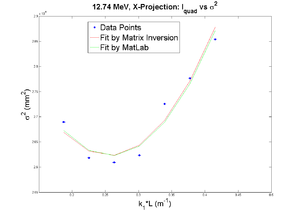
12.74 MeV
Fitted Gaussian for whole image x-projection:
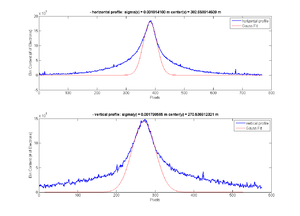
Gaussian fitted for part 1 of the image
Fitted Gaussian for part 1 of the image
xl = 362;% center at 382
xr = 404;
yl = 241;% center at 271
yr = 301;
xl: x left, xr: x right. yl: y left, yr: y right.
x-projection:
Gaussian fitted for part 2 of the image
Fitted Gaussian for part 2 of the image
xl = 342;% center at 382
xr = 424;
yl = 241;% center at 271
yr = 301;
x-projection:
Gaussian fitted for part 3 of the image
Fitted Gaussian for part 3 of the image
xl = 342;% center at 382
xr = 424;
yl = 221;% center at 271
yr = 321;
x-projection:
Gaussian fitted for part 4 of the image
Fitted Gaussian for part 4 of the image
xl = 322;% center at 382
xr = 444;
yl = 221;% center at 271
yr = 321;
x-projection:
Analysis with root
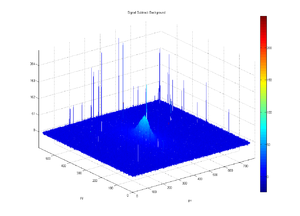
Q1_Scan, 42mA peak current, Scan Coil Current at positive 1.8_Amp
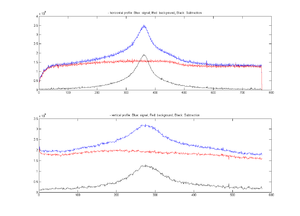
Back grounds
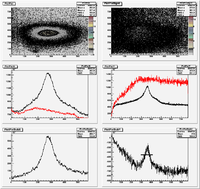
The red line is the background above which seems to be larger than the signal. Why?
Below I zoom in on channel 250 where you can see that for this channel the background is larger. I then plot, on the right, all the elements along the x direction what are added up to get the values on the right.
Why isn't the addition making sense?
Q6_Scan, 42mA peak current, Scan Coil Current at negative 2.5_Amp
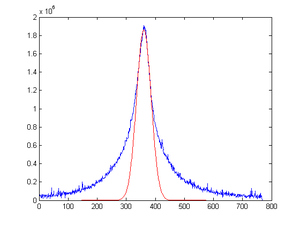
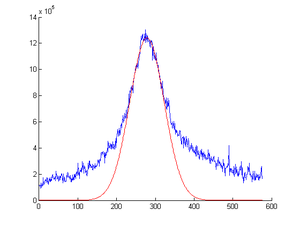
Lorentzian Fitting
Basic MATLAB Codes to fit Lorentzian:
File:Trial my Lorentzian fit.txt
My MATLAB Fit code for beam
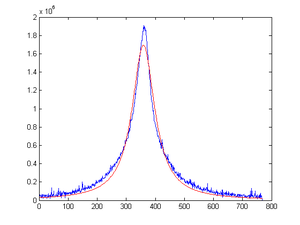
Here is an example fitting:
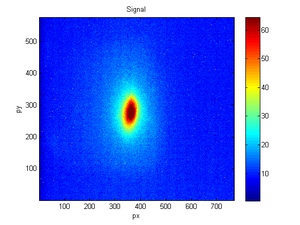
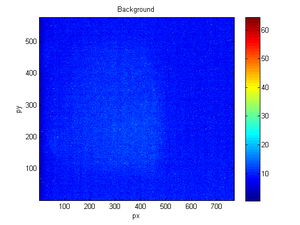
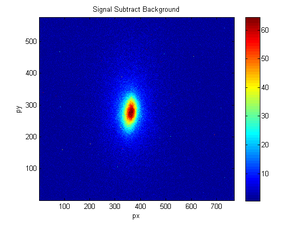
| Signal | Background | fit |
 |
 |
|
| height of the peak | location of the peak | half-width at half-maximum (HWHM) |
| 1.6935e+006 | 358.9910 | 45.4280 |
If we were to apply the relation of the Gaussian rms to its FWHM to Lorentzian, we will get the sigma (or rms) of Lorentzian to be:
Super Gaussian Fitting
Beam Distributions Beyond RMS: File:Beam Distributions Beyond RMS.pdf
Basic MATLAB Codes to fit Super Gaussian:
File:Trial my Super Gaussian fit.txt
My MATLAB Fit code for beam
File:My Super Gaussian fit.txt
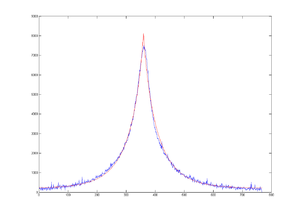
Here is an example fitting:
| Signal | Background | fit |
 |
 |
|
| base | Amplitude | center |
| 202 | 8.0480e+003 | 359.6730 |
| sigma_0 | N | sigma |
| 20.92 | 0.8494 | 38.56 |
If we were to apply the relation of the Gaussian rms to its FWHM to Lorentzian, we will get the sigma (or rms) of Lorentzian to be:
This is very close to the sigma we got from Super Gaussian, which is 38.56
Results
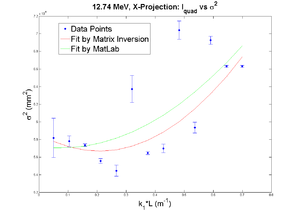
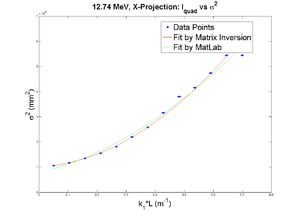
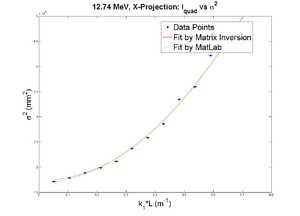
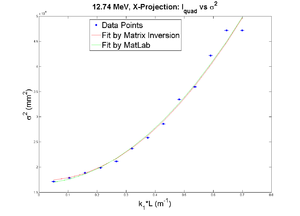
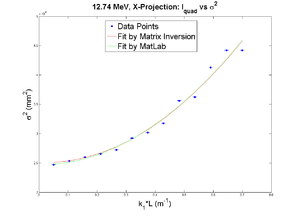
Q1
Positive Current, X projection
1st fit
2nd fit after cut off some points
Q4
Did not reach minimum.