Difference between revisions of "GradFinalLab RS"
| Line 40: | Line 40: | ||
| − | The actual measured values of high and low output voltages | + | The actual measured values of high and low output voltages (they do not really equal to <math>\pm V_{cc}</math>) are: |
# <math>V_{out_1} = (+11.06\pm0.01)\ V</math> | # <math>V_{out_1} = (+11.06\pm0.01)\ V</math> | ||
| Line 46: | Line 46: | ||
| − | Substituting all | + | |
| + | Substituting all quantities in the formulas above: | ||
<math>R_{123} = (1.01\pm 0.01)\ k\Omega || (1.01\pm 0.01)\ k\Omega || (5.10\pm 0.05)\ k\Omega = (0.459\pm 0.003)\ k\Omega</math> | <math>R_{123} = (1.01\pm 0.01)\ k\Omega || (1.01\pm 0.01)\ k\Omega || (5.10\pm 0.05)\ k\Omega = (0.459\pm 0.003)\ k\Omega</math> | ||
| − | <math>V_2 = \frac{(0.459\pm 0.003)\ k\Omega}{(1.01\pm 0.01)\ k\Omega}(11.90\pm 0.01)\ V + \frac{(0.459\pm 0.003)\ k\Omega}{(5.10\pm 0.05)\ k\Omega}(11.06\ pm 0.01)\ V</math> | + | <math>V_2 = \frac{(0.459\pm 0.003)\ k\Omega}{(1.01\pm 0.01)\ k\Omega}(11.90\pm 0.01)\ V + \frac{(0.459\pm 0.003)\ k\Omega}{(5.10\pm 0.05)\ k\Omega}(11.06\pm 0.01)\ V</math> |
| + | |||
| + | <math>V_2^' = \frac{(0.459\pm 0.003)\ k\Omega}{(1.01\pm 0.01)\ k\Omega}(11.90\pm 0.01)\ V - \frac{(0.459\pm 0.003)\ k\Omega}{(5.10\pm 0.05)\ k\Omega}(10.54\pm0.01)\ V</math> | ||
| + | |||
| + | and doing math and propagating errors we end up with the following predicted threshold voltages: | ||
| − | + | 1) If the output voltage is high the threshold voltage are: | |
| − | + | <math>V_2 = (6.41\pm 0.07)\ V | |
| − | + | 1) If the output voltage is low the threshold voltage are: | |
| − | <math>V_2 | + | <math>V_2 = (4.46\pm 0.06)\ V |
==Compare the threshold values to what is expected.== | ==Compare the threshold values to what is expected.== | ||
Revision as of 03:14, 27 April 2011
Construct a Schmitt Trigger using the 741 Op Amp
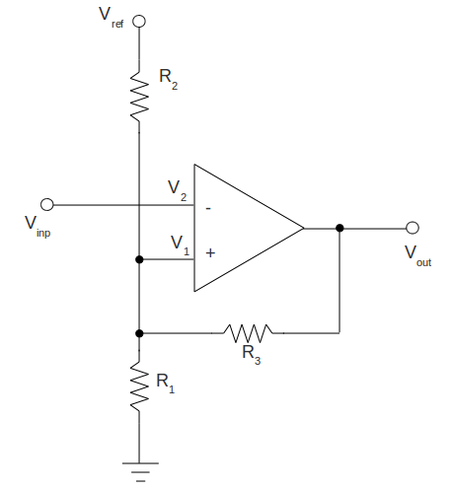
Draw the Schmitt Trigger circuit you constructed. Identify the values of all components
To construct the circuit above I am going to use the following components and voltages:
Graph as a function of . Is there a hysteresis loop?
Identify the input voltage threshold levels at which a will produce
The theory does say (ch. 10.19 The Schmitt Trigger R. Simpson "Introductory electronics for scientists and engineers"):
1) if the output is high:
2) if the output is low:
where
The actual measured values of high and low output voltages (they do not really equal to ) are:
Substituting all quantities in the formulas above:
and doing math and propagating errors we end up with the following predicted threshold voltages:
1) If the output voltage is high the threshold voltage are:
<math>V_2 = (6.41\pm 0.07)\ V
1) If the output voltage is low the threshold voltage are:
<math>V_2 = (4.46\pm 0.06)\ V
Compare the threshold values to what is expected.
Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement