Lab 23 RS

Go Back to All Lab Reports

Inverting OP Amp

1. Construct the inverting amplifier according to the wiring diagram below.

Here is the data sheet for the 741 Op Amp

File:LM741CN OpAmp.pdf

Use [math]R_1 = 1k\Omega[/math] and [math]R_2 = 10 k\Omega[/math] as starting values.

2. Insert a 0.1 [math]\mu[/math]F capacitor between ground and both Op Amp power supply input pins. The Power supply connections for the Op amp are not shown in the above circuit diagram, check the data sheet.

Gain measurements

1.) Measure the gain as a function of frequency between 100 Hz and 2 MHz for three values of [math]R_2[/math] = 10 k[math]\Omega[/math], 100 k[math]\Omega[/math], 1M[math]\Omega[/math]. Keep [math]R_1[/math] at [math]1k\Omega[/math].

I have used the following values of [math]R_1[/math] and [math]R_2[/math] (as was suggested by Dr Forrest at the lecture)

[math]R_1 = (10.02 \pm 0.02)\ k\Omega[/math]
a) [math]R_2 = (99.0 \pm 0.2)\ k\Omega[/math]
b) [math]R_2 = (198.5 \pm 0.2)\ k\Omega[/math]
c) [math]R_2 = (800.0 \pm 2.0)\ k\Omega[/math]

So my theoretical gain of OP Amp would be:

a) Gain1[math]= \frac{R_2}{R_1} = \frac{99.0 \pm 0.2}{10.02 \pm 0.02} = (9.88 \pm 0.03)[/math]

b) Gain2[math]= \frac{R_2}{R_1} = \frac{198.5 \pm 0.2}{10.02 \pm 0.02} = (19.81 \pm 0.04)[/math]

c) Gain3[math]= \frac{R_2}{R_1} = \frac{800.0 \pm 2.0}{10.02 \pm 0.02} = (79.84 \pm 0.26)[/math]

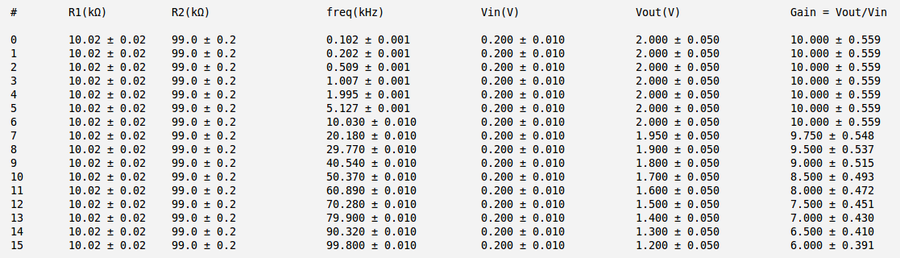
Below is my measurements and gain calculation for the case a) [math]R_1 = (10.02 \pm 0.02)\ k\Omega[/math] and [math]R_2 = (99.0 \pm 0.2)\ k\Omega[/math]

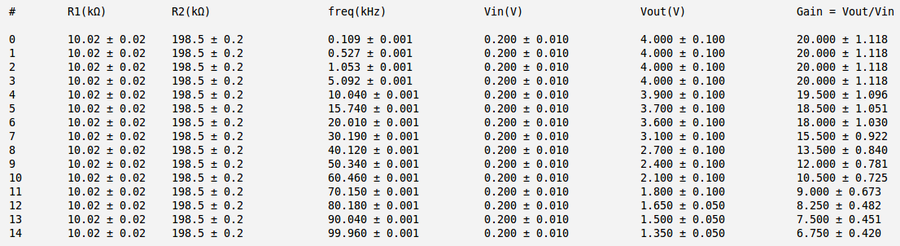
Below is my measurements and gain calculation for the case b) [math]R_1 = (10.02 \pm 0.02)\ k\Omega[/math] and [math]R_2 = (198.5 \pm 0.2)\ k\Omega[/math]

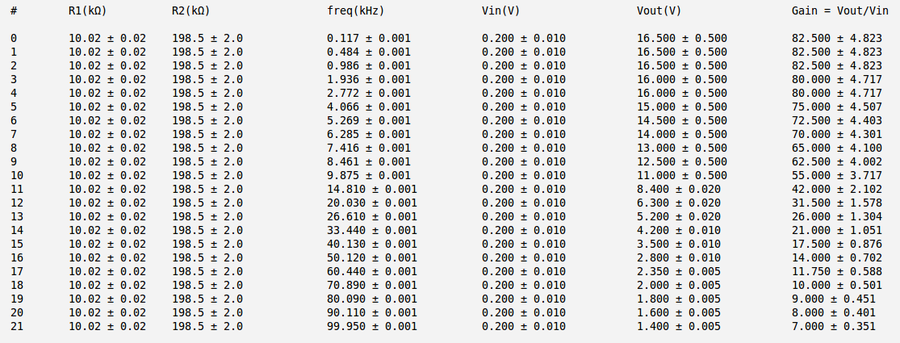
Below is my measurements and gain calculation for the case c) [math]R_1 = (10.02 \pm 0.02)\ k\Omega[/math] and [math]R_2 = (800.0 \pm 2.0)\ k\Omega[/math]

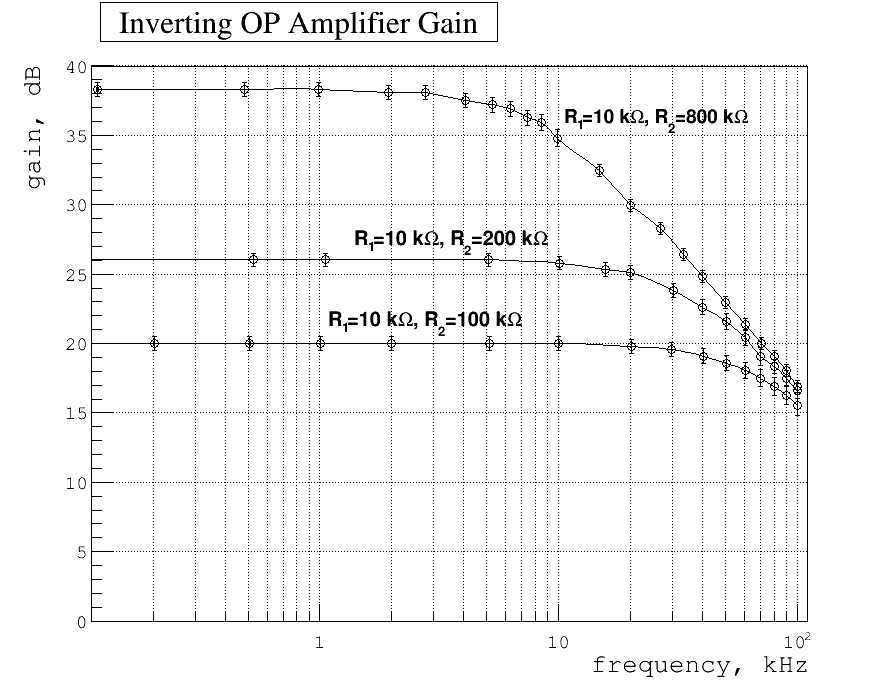
2.) Graph the above measurements with the Gain in units of decibels (dB) and with a logarithmic scale for the frequency axis.

Below my plot of gain as function of frequency. Here

[math]G_{dB} \left(\frac{V_{out}}{V_{in}}\right) = 20\cdot \log_{10} {\frac{V_{out}}{V_{in}}}[/math]

Here the error calculation as usual and for this specific case is:

[math]dG_{dB}(x) = \frac{\partial G_{dB}(x)}{\partial x}\cdot dx = \frac{20}{x\ \ln 10}\cdot dx[/math]

where [math]x[/math] and [math]dx[/math] are corresponding gain and error of gain from the tables above

Impedance

Input Impedance

1. Measure [math]R_{in}[/math] for the 10 fold and 100 fold amplifier at ~100 Hz and 10 kHz frequency.

I am going to measure the input and output impedance of my amplifier using the following equivalent circuit:

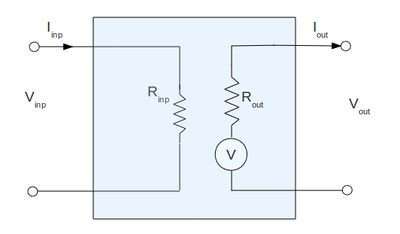
where the shaded region is my actual amplifier constructed before:

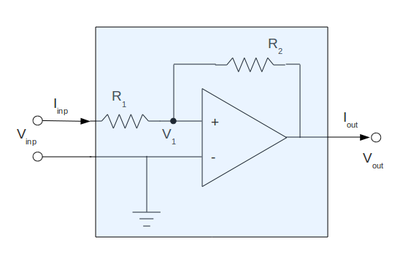
From equivalent circuit the input impedance is:

[math]R_{inp} = \frac{V_{inp}}{I_{inp}}[/math]

and from my real circuit inside the shaded region:

[math]I_{inp} = \frac{V_{inp}-V_1}{R_1}[/math]

so finally my input impedance becomes:

[math]R_{inp} = \frac{V_{inp}}{V_{inp}-V_1}\ R_1[/math]

Below is the table with my measurements and input impedance calculations for four asked different cases. Here I have used the meter instead of oscilloscope to reduce the error in my measurements of input voltage.

As we can see the input impedance equals the resistor value [math]R_1[/math] for low frequency [math]f=100\ Hz[/math] and increase up to [math]33\ k\Omega[/math] for high frequency [math]f=10\ kHz[/math].

Output Impedance

1. Measure [math]R_{out}[/math] for the 10 fold and 100 fold amplifier at ~100 Hz and 10 kHz frequency. Be sure to keep the output ([math]V_{out}[/math]) undistorted

Again the equivalent circuit I am going to use is:

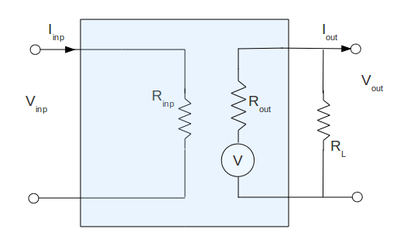
And my output impedance is:

[math]V_{out} = V - I_{out}\cdot R_{out}[/math]

But now I am going to use the load resistor [math]R_L[/math] to measure the output circuit:

[math]I_{out} = \frac{V_{out}}{R_L}[/math]

By graphing the current on the x-axis and the measured voltage [math]V_{out}[/math] on the y-axis for several values of the load resistance [math]R_L[/math] we can find the output internal impedance of our amplifier as the slope of the line [math]V_{out}=V_A - I_{out}\cdot R_{out}[/math]

Below are my measurements and current calculation for different cases. Here I have used the meter instead of oscilloscope to reduce the error in my measurements of output voltage.

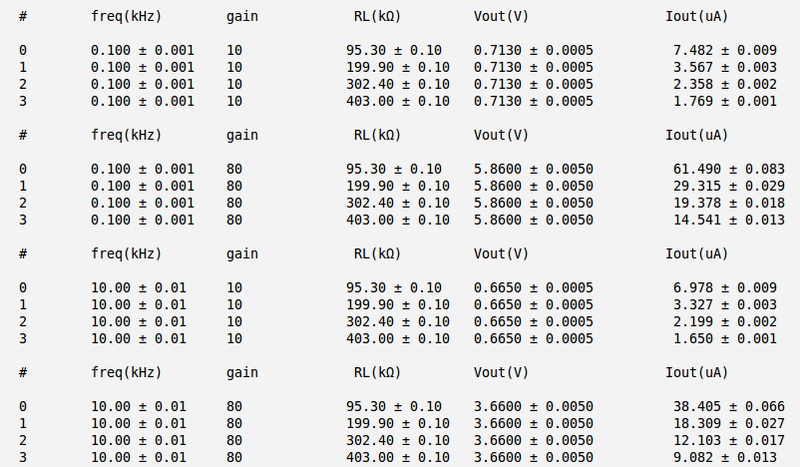
Below are the plots of the [math]V_{out}[/math] as function of [math]I_{out}[/math]

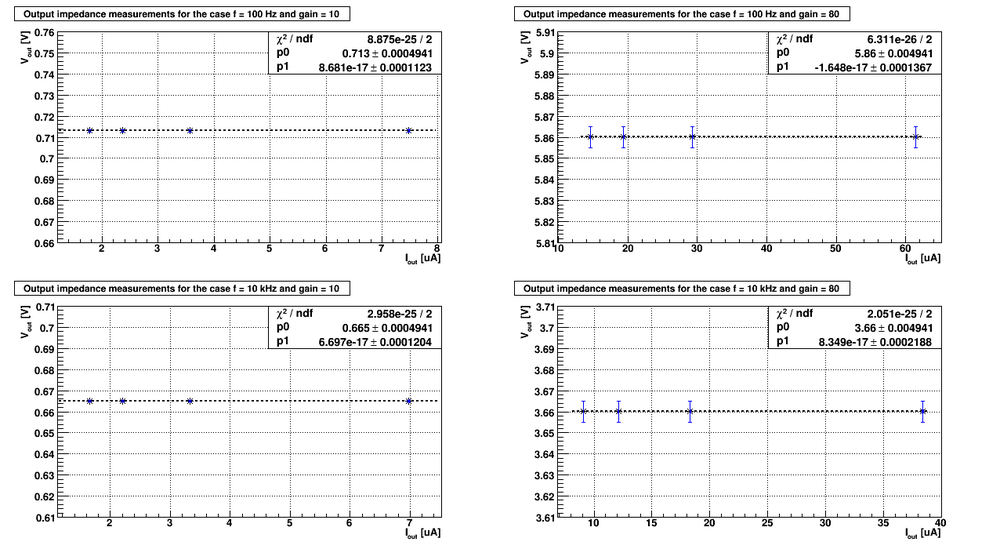
As it follows from the plots above the output impedance (the slope of the line) are:

1) 10 fold amplifier at ~100 Hz frequency: [math]R_{out} = (8.68\cdot 10^{-11} \pm 112.3)\ \Omega[/math]
2) 10 fold amplifier at ~10 kHz frequency: [math]R_{out} = (6.70\cdot 10^{-11} \pm 120.4)\ \Omega[/math]
3) 80 fold amplifier at ~100 Hz frequency: [math]R_{out} = (-1.65\cdot 10^{-11} \pm 136.7)\ \Omega[/math]
3) 80 fold amplifier at ~10 kHz frequency: [math]R_{out} = (8.35\cdot 10^{-11} \pm 218.8)\ \Omega[/math]

As we can see the output impedance is essentially the zero. Unfortunately the calculated error is up to [math]220.\ \Omega[/math]. To get the better results I need dramatically improve my measurements, and particularly, improve the measured error in [math]V_{out}[/math]

[math]V_{io}[/math] and [math]I_{B}[/math]

[math]V_{out}= -\frac{R_2}{R_1} V_{in} + \left ( 1 + \frac{R_2}{R_1}\right)V_{io} + R_2 I_B[/math]

Use the above equation and two measurements of [math]V_{out}[/math], [math]R_1[/math], and [math]R_2[/math] to extract [math]V_{io}[/math] and [math]I_B[/math]. I will use two different values of [math]R_2[/math] to make two different measurements. [math] V_{in}[/math]=0 (grounded).

Below are my measurements. I have used the meter instead of oscilloscope to reduce my measured error in measured small output voltage.

1) [math]f=1\ kHz[/math] [math]R_1 = (10.06 \pm 0.01)\ k\Omega[/math], [math]R_2 = (99.5 \pm 0.1)\ k\Omega[/math]:  [math]V_{in}=(0.05 \pm 0.05)\ mV[/math] [math]V_{out}=(6.9 \pm 0.05)\ mV[/math]
2) [math]f=1\ kHz[/math] [math]R_1 = (10.06 \pm 0.01)\ k\Omega[/math], [math]R_2 = (199.6 \pm 0.1)\ k\Omega[/math]:  [math]V_{in}=(0.05 \pm 0.05)\ mV[/math] [math]V_{out}=(14.1 \pm 0.05)\ mV[/math]

Now I can construct 2 equations with 2 unknowns [math]V_{io}[/math] and [math]I_B[/math].

[math] (1 + (99.5 \pm 0.1)/(10.06 \pm 0.01))\cdot V_{io} + (99.5 \pm 0.1)\ k\Omega \cdot I_B = (6.9 \pm 0.05)\ mV[/math]

[math] (1 + (199.6 \pm 0.1)/(10.06 \pm 0.01))\cdot V_{io} + (199.6 \pm 0.1)\ k\Omega \cdot I_B = (14.1 \pm 0.05)\ mV[/math]

or

[math] (10.891 \pm 0.014)\cdot V_{io} + (99.5 \pm 0.1)\cdot 10^3\ I_B = (6.9 \pm 0.05)\cdot 10^{-3}[/math]

[math] (20.841 \pm 0.022)\cdot V_{io} + (199.6 \pm 0.1)\cdot 10^3\ I_B =(14.1 \pm 0.05)\cdot 10^{-3}[/math]

with [math]V_{io}[/math] given in Volts and [math]I_B[/math] given in Amperes.

To solve these equations will use the matrix method. Let's do it in general to be able to handle the error propagation. We have:

[math]\left( \begin{array}{cc} a_1 & b_1\\ a_2 & b_2 \end{array} \right)\left( \begin{array}{c} V_{io} \\ I_B \end{array} \right) = \left( \begin{array}{c} c_1 \\ c_2 \end{array} \right)[/math]

and the two solutions are:

[math]V_{io} = \frac{\left| \begin{array}{cc} c_1 & b_1\\c_2 & b_2 \end{array} \right| }{\left| \begin{array}{cc} a_1 & b_1\\a_2 & b_2 \end{array} \right| } = \frac{c_1b_2-c_2b_1}{a_1b_2-a_2b_1}\ \ [/math]: [math]I_B = \frac{\left| \begin{array}{cc} a_1 & c_1\\a_2 & c_2 \end{array} \right| }{\left| \begin{array}{cc} a_1 & b_1\\a_2 & b_2 \end{array} \right| } = \frac{a_1c_2-a_2c_1}{a_1b_2-a_2b_1}[/math]

Substituting the corresponding coefficients:

[math]V_{io} = \frac{c_1b_2-c_2b_1}{a_1b_2-a_2b_1} = \frac{(6.9 \pm 0.05)\cdot 10^{-3}\cdot (199.6 \pm 0.1)\cdot 10^3 - (14.1 \pm 0.05)\cdot 10^{-3}\cdot (99.5 \pm 0.1)\cdot 10^3}{(10.891 \pm 0.014)\cdot (199.6 \pm 0.1)\cdot 10^3 - (20.841 \pm 0.022)\cdot (99.5 \pm 0.1)\cdot 10^3}[/math]

[math]I_B = \frac{a_1c_2-a_2c_1}{a_1b_2-a_2b_1} = \frac{(10.891 \pm 0.014)\cdot (14.1 \pm 0.05)\cdot 10^{-3} - (20.841 \pm 0.022)\cdot (6.9 \pm 0.05)\cdot 10^{-3}}{(10.891 \pm 0.014)\cdot (199.6 \pm 0.1)\cdot 10^3 - (20.841 \pm 0.022)\cdot (99.5 \pm 0.1)\cdot 10^3}[/math]

and by doing math and handling the error propagation we find:

[math]V_{io} = (-0.257 \pm 0.114)\ mV [/math]
[math]I_B = (97.5 \pm 12.0)\ nA [/math]

[math]I_{io}[/math]

Now we will put in a pull up resistor [math]R_3= \frac{R_1 R_2}{R_1+R_2}[/math](measured) as shown below.

I have constructed [math]R_3[/math] from two resistor in parallel identical to my [math]R_1[/math] and [math]R_2[/math] used in my initial circuit.

a) [math]R_3= (10\ k\Omega)||(100\ k\Omega) = (9.20 \pm 0.01)\ k\Omega[/math](measured)
b) [math]R_3= (10\ k\Omega)||(200\ k\Omega) = (9.66 \pm 0.01)\ k\Omega[/math](measured)

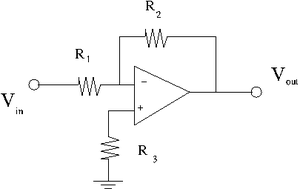
Instead of the current [math]I_B[/math] we have the current [math]I_{io}[/math]

[math]V_{out}= -\frac{R_2}{R_1} V_{in} + \left ( 1 + \frac{R_2}{R_1}\right)V_{io} + R_2 I_{io}[/math]

Use the same technique and resistors from the previous section to construct 2 equations and 2 unknowns and extract [math]I_{io}[/math], keep [math]V_{in}[/math]=0.

Below are my measurements. I have used the meter instead of oscilloscope to reduce my measured error in measured small output voltage. [math]f=1\ kHz[/math].

1) [math]R_1 = (10.06\pm0.01)\ k\Omega[/math],[math]R_2 = (99.5\pm0.1)\ k\Omega[/math],[math]R_3 = (9.20\pm0.01)\ k\Omega[/math]:  [math]V_{in}=(0.05 \pm 0.05)\ mV[/math],[math]V_{out}=(-1.5 \pm 0.05)\ mV[/math]
2) [math]R_1 = (10.06\pm0.01)\ k\Omega[/math],[math]R_2 = (199.6\pm0.1)\ k\Omega[/math],[math]R_3 = (9.20\pm0.01)\ k\Omega[/math]:  [math]V_{in}=(0.05 \pm 0.05)\ mV[/math],[math]V_{out}=(-2.8 \pm 0.05)\ mV[/math]

and to equations becomes:

[math] (10.891 \pm 0.014)\cdot V_{io} + (99.5 \pm 0.1)\cdot 10^3\ I_{io} = (-1.5 \pm 0.05)\cdot 10^{-3}[/math]

[math] (20.841 \pm 0.022)\cdot V_{io} + (199.6 \pm 0.1)\cdot 10^3\ I_{io} =(-2.8 \pm 0.05)\cdot 10^{-3}[/math]

with [math]V_{io}[/math] given in Volts and [math]I_B[/math] given in Amperes.

Substituting the corresponding coefficients into general solutions derived above:

[math]V_{io} = \frac{c_1b_2-c_2b_1}{a_1b_2-a_2b_1} = \frac{(-1.5 \pm 0.05)\cdot 10^{-3}\cdot (199.6 \pm 0.1)\cdot 10^3 - (-2.8 \pm 0.05)\cdot 10^{-3}\cdot (99.5 \pm 0.1)\cdot 10^3}{(10.891 \pm 0.014)\cdot (199.6 \pm 0.1)\cdot 10^3 - (20.841 \pm 0.022)\cdot (99.5 \pm 0.1)\cdot 10^3}[/math]

[math]I_{io} = \frac{a_1c_2-a_2c_1}{a_1b_2-a_2b_1} = \frac{(10.891 \pm 0.014)\cdot (-2.8 \pm 0.05)\cdot 10^{-3} - (20.841 \pm 0.022)\cdot (-1.5 \pm 0.05)\cdot 10^{-3}}{(10.891 \pm 0.014)\cdot (199.6 \pm 0.1)\cdot 10^3 - (20.841 \pm 0.022)\cdot (99.5 \pm 0.1)\cdot 10^3}[/math]

and by doing math and handling the error propagation we find:

[math]V_{io} = (-0.208 \pm 0.112)\ mV [/math]
[math]I_{io} = (7.7 \pm 11.2)\ nA [/math]

As we can see [math]I_{io}[/math] reduced from about [math]100\ nA[/math] (case without [math]R_3[/math]) down to [math]7\ nA[/math] (case with [math]R_3[/math]). And it is exactly what we are expecting because it is what the resistor [math]R_3[/math] is doing. Unfortunately me error becomes up to [math]11\ nA[/math], but even inside this error uncertainty my current [math]I_{io}[/math] has gone down.

The offset Null Circuit

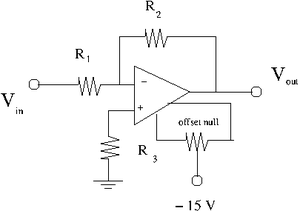
1) Construct the offset null circuit above.

I have used the gain 20 case with resistors values from previous section:

[math]R_1 = (10.06\pm0.01)\ k\Omega[/math], [math]R_2 = (199.6\pm0.1)\ k\Omega[/math], [math]R_3 = (9.20\pm0.01)\ k\Omega[/math]

because it's the most worse case for I would like to minimize using potentiometer (my initial [math]V_{out}=(-2.8 \pm 0.05)\ mV[/math].)

2) Adjust the potentiometer to minimize [math]V_{out}[/math] with [math]V_{in}=0[/math].

3) Use a scope to measure the output noise.

Using potentiometer I was able to reduce my [math]V_{out}[/math] up to zero with the noise:

[math](\Delta V_{out})_{RMS} = \frac{1.0\ mV}{2\sqrt{2}} = 0.35\ mV[/math]

Capacitors

Revert back to the pull up resistor

Capacitor in parallel with [math]R_2[/math]

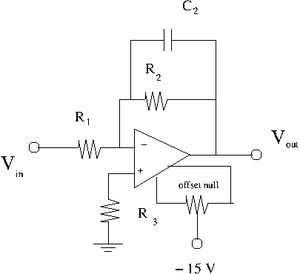
1. Select a capacitor such that[math] \frac{1}{\omega C_2} \approx R_2[/math] when [math]\omega[/math]= 10 kHz.
2. Add the capacitor in parallel to [math]R_2[/math] so you have the circuit shown above.
3. Use a pulse generator to input a sinusoidal voltage [math]V_{in}[/math]
4. Measure the Gain as a function of the [math]V_{in}[/math] frequency and plot it.

Capacitor in series with R_1

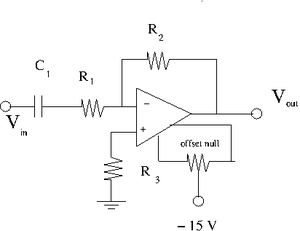
1. Select a capacitor such that[math] \frac{1}{\omega C_2} \approx R_1[/math] when [math]\omega[/math]= 1 kHz.
2. Add the capacitor in series to [math]R_1[/math] so you have the circuit shown above.
3. Use a pulse generator to input a sinusoidal voltage [math]V_{in}[/math]
4. Measure the Gain as a function of the [math]V_{in}[/math] frequency and plot it.

Slew rate

Measure the slew and compare it to the factory spec.

Power Supply Rejection Ratio

1. Set [math]V_{in}[/math] = 0.
2. Measure [math]V_{out}[/math] while changing [math]V_{cc}[/math]

Output voltage RMS noise [math]\Delta V_{out}^{RMS}[/math]

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement