Lab 14 RS

Go Back to All Lab Reports

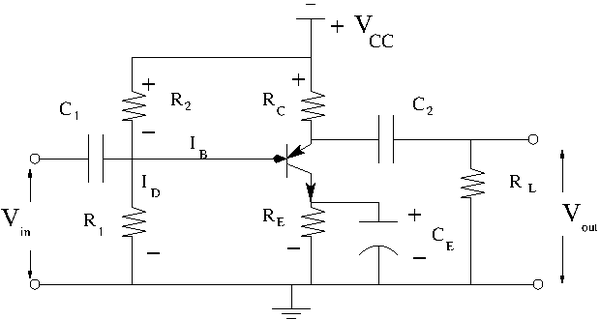
The Common Emitter Amplifier

Circuit

Construct the common emitter amplifier circuit below according to your type of emitter.

Calculate all the R and C values to use in the circuit such that

a. Try $R_B \approx 220 \Omega$ and $I_C \approx 100 \mu A$

b. $I_C \gt 0.5$ mA DC with no input signal

c. $V_{CE} \approx V_{CC}/2 \gt 2$ V

d. $V_{CC} \lt V_{CE}(max)$ to prevent burnout

e. $V_{BE} \approx 0.6 V$

f. $I_D \approx 10 I_B \lt 1$ mA

Let's $V_{CC} = 11\ V$, $R_E = 0.2\ k\Omega$ and $R_C = 2.0\ k\Omega$.

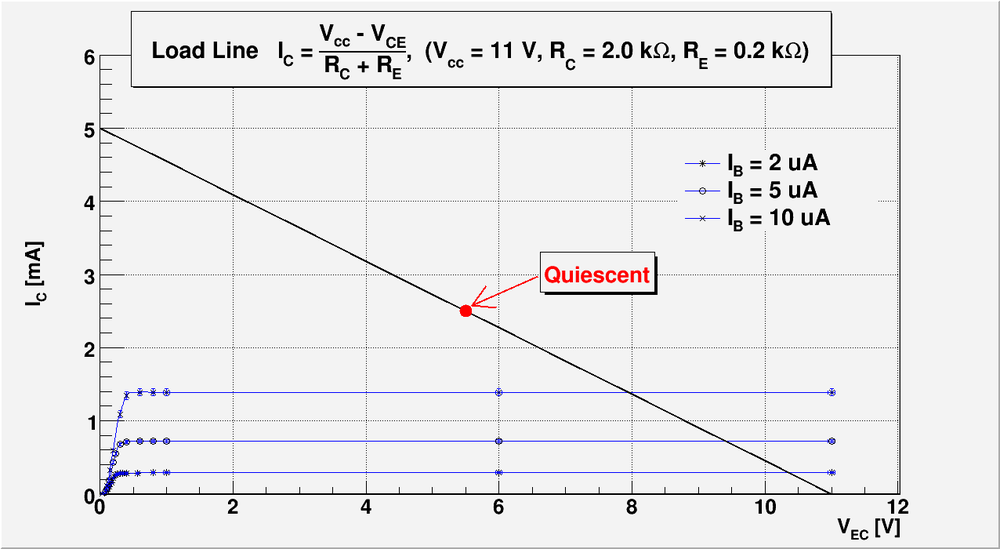
The load line equation becomes:

[math]I_C = \frac{V_{CC}-V_{CE}}{R_E+R_C} = \frac{(11 - V_{CE})\ V}{2.2\ k\Omega} [/math]

Draw a load line using the $I_{C}$ -vs- $I_{EC}$ from the previous lab 13. Record the value of $h_{FE}$ or $\beta$.

On the plot below I overlay the output transistor lines (from the previous lab report #13) and the Load Line calculated above.

My $\beta \approx 170$ based on my previous lab report #13

Set a DC operating point $I^{\prime}_C$ so it will amplify the input pulse given to you. Some of you will have sinusoidal pulses others will have positive or negative only pulses.

I will set up my operating point in the middle of the load line:

[math]I_C = 2.5\ mA[/math], [math]V_{EC} = 5.5\ V[/math].

Let's calculate all bias voltage needed to set up this operating point. Because the knowing of $V_{BE}$ and $\beta$ is very important for this calculation I did the preliminary set up to measure this quantities. They are the only parameters which depends from transistor. I was able to find:

[math]V_{BE} = 0.68\ V[/math]

[math]\beta = 173[/math]

Now

[math]V_E = I_E \cdot R_E = 2.5\ mA \cdot 0.2\ k\Omega = 0.5\ V[/math]
[math]V_B = V_E + V_B = (0.50 + 0.68)\ V = 1.18\ V[/math]

To set up the operating point above we need to set up $V_{B} = 1.18\ V$.

We have:

[math]I_B = \frac{I_C}{\beta} = \frac{2.5\ mA}{173} = 14.4\ uA[/math].

To get operating point independent of the transistor base current we want $I_{R1} \gg\ I_B$

Let's $I_{R1} = 590\ uA \gg\ I_B = 14.4\ uA$

So

[math]R_1 = \frac{V_B}{I_1} = \frac{1.18\ V}{590\ uA} = 2\ k\Omega[/math]

And $R_2$ we can find from Kirchhoff Voltage Low:

[math]V_{CC} = I_2 \cdot R_2 + V_B[/math].

and Kirchhoff Current Low:

[math]I_2 = I_1 + I_B[/math]

So

 [math]R_2 = \frac{V_{CC}-V_B}{I_1+I_B} = \frac{(11-1.18)\ V}{(590 + 14.4)\ mA} = 16.25\ k\Omega[/math]

I tried to adjust my calculation by varying the fee parameters $V_{cc}$ and $I_1$ to get good values for resistors I can easily to set up.

Measure all DC voltages in the circuit and compare with the predicted values.(10 pnts)

My predicted DC voltage are:

We have from operating point:

[math]V_{EC} = 10\ V[/math] 
[math]I_C \approx I_E = 5\ mA[/math]

And because we have silicon transistor:

[math]V_{BE} = 0.6\ V [/math]

Now

[math]V_E = I_E \cdot R_E = 5\ mA \cdot 200\ \Omega = 1\ V[/math]
[math]V_C = V_E + V_{EC} = (1 + 11)\ V = 12\ V[/math]
[math]V_B = V_E + V_{BE} = (1 + 0.6)\ V = 1.6\ V[/math]

My measured DC voltage are:

[math]V_{EC} = (11.25 \pm 0.01)\ V[/math]
[math]V_{BE} = (0.69 \pm 0.01)\ V [/math]

[math]V_E = (0.88 \pm 0.01)\ V[/math]
[math]V_C = (12.11 \pm 0.01)\ V[/math]
[math]V_B = (1.56 \pm 0.01)\ V[/math]

First note that my $V_B = (1.56 \pm 0.01)\ V$ is close to predicted values $V_B = 1.6\ V$.

Also note that my $V_{EC} = (11.25 \pm 0.01)\ V$ is a little higher than my initial operating point $V_{EC} = 10\ V$. The main reason is that my actual values of $V_{BE} = (0.69 \pm 0.01)\ V$ instead of $V_{BE} = 0.6\ V$ as I was assumed initially. That will reduce my $V_E$ voltage that reduce my $I_C$ current. So I will shift to right my operating point from $I_C = 5\ mA$ to lower values and correspondingly will increase my $V_{EC}$.

By direct measurements my operating point now is $I_C = (4.34 \pm 0.01)\ mA$ and $V_{EC} = (11.25 \pm 0.01)\ V$

Let's check do my operating point is still on my load line. I have $R_E = (0.20 \pm 0.01)\ k\Omega$, $R_C = (1.80 \pm 0.01)\ k\Omega$. So from load line equation:

[math]I_C = \frac{V_{CC}-V_{CE}}{R_E+R_C} = \frac{((20.01\pm 0.01)-(11.25\pm 0.01))\ V}{((1.80 \pm 0.01))+ (0.20 \pm 0.01))\ k\Omega} = (4.38 \pm 0.04)\ mA[/math].

So my operating point lies in my load line within experimental error.

Measure $R_{in}$ and $R_{out}$ at about 1 kHz and compare to the theoretical value.(10 pnts)

How do you do this? Add resistor in front of $C_1$ which you vary to determine $R_{in}$ and then do a similar thing for $R_{out}$ except the variable reistor goes from $C_2$ to ground.

Questions

1. Why does a flat load line produce a high voltage gain and a steep load line a high current gain? (10 pnts)
2. What would be a good operating point an an $npn$ common emitter amplifier used to amplify negative pulses?(10 pnts)
3. What will the values of $V_C$, $V_E$ , and $I_C$ be if the transistor burns out resulting in infinite resistance. Check with measurement.(10 pnts)
4. What will the values of $V_C$, $V_E$ , and $I_C$ be if the transistor burns out resulting in near ZERO resistance (ie short). Check with measurement.(10 pnts)
5. Predict the change in the value of $R_{in}$ if $I_D$ is increased from 10 $I_B$ to 50 $I_B$(10 pnts)
6. Sketch the AC equivalent circuit of the common emitter amplifier.(10 pnts)

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement