Lab 9 RS

Go Back to All Lab Reports

Lab 9: Diode Circuits

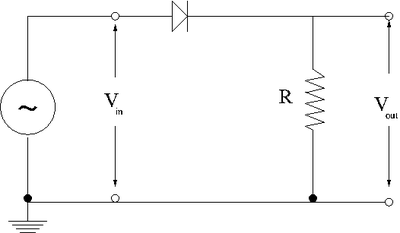
Clipping Circuit

1.) Construct the circuit shown below using a silicon diode.

2.) Use a sine wave generator to drive the circuit so [math]V_{in} = V_0 \cos(2 \pi \nu t)[/math] where [math]V_0 = 0.1[/math] V and [math] \nu[/math] = 1kHz. (20 pnts)

3.)Based on your observations using a oscilloscope, sketch the voltages [math]V_{in}[/math] and [math]V_{out}[/math] as a function of time.

4.)Do another sketch for[math] V_0[/math] = 1.0 V and another for 10.0 V (DONT LET ANY SMOKE OUT!). (20 pnts)

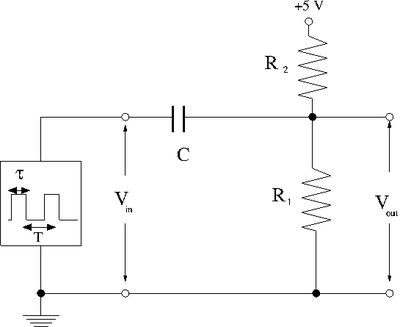
Differentiating Circuit with clipping

1. Construct the circuit below.

1. Select [math]R_1[/math] and [math]R_2[/math] such that the current from the +5V DC source is less than 1.0 mA and the DC voltage at [math]V_{out}[/math] is 3 V when there is no input pulse.

Because we want to keep the current below [math]1\ mA[/math] and using [math]I = \frac{V}{R_1+R_2} \leq 1\ mA \ \ \ \rightarrow [/math]. Solving this inequality we get the first condition for [math]R_1\lt \math\gt and \lt math\gt R_2\lt \math\gt \lt math\gt 1)\ \ R_1+R_2 \geq \frac{5\ V}{1\ mA} = 5\ k\Omega[/math]

Also because we want [math]V_{out} = 3\ V[/math] and using [math]V_{out} = V_{in} \frac{R_2}{R_1+R_2} \Longrightarrow \frac{R_2}{R_1+R_2} = frac{V_{out}}{V_{in}} = frac{3\ V}{5\ V} [/math]. Solving this equation we get the second condition [math]R_1\lt \math\gt and \lt math\gt R_2\lt \math\gt \lt math\gt 2)\ \ R_2 = 1.5\ R_1[/math]

1. Select a capacitor [math](C)[/math]and a pulse width \[math]tau[/math] to form a differentiating circuit for the pulse from the signal generator. Hint: [math]R_{12}C \ll \tau[/math].
2. plot [math]V_{in}[/math] and [math]V_{out}[/math] as a function of time using your scope observations. (20 pnts)
3. Now add the diode circuit from part 1 to prevent [math]V_{out}[/math] from rising above +5 V. Sketch the new circuit below.
4. plot [math]V_{in}[/math] and [math]V_{out}[/math] as a function of time with the diode circuit you added using your scope observations. (the diode should clip off positive spikes)(20 pnts)

Questions

1. Explain your results in parts 1 & 2 in terms of the diode turn-on voltage. (20 pnts)

Forest_Electronic_Instrumentation_and_Measurement Go Back to All Lab Reports