Difference between revisions of "Lab 5 RS"
Jump to navigation
Jump to search
| Line 61: | Line 61: | ||
==Questions== | ==Questions== | ||
| − | + | #What is the bandwidth of the above circuit? (5 pnts) | |
| + | |||
| + | From the plot above we have <math>\left(\frac{V_{out}}{_{Vin}} \right)_{max} = 0.0138 </math> | ||
| + | |||
| + | The bandwidth defined as the width from <math>\omega_1</math> to <math>\omega_2</math> where the amplitude of signal drop down to <math>\frac{1}{\sqrt{2}}</math>. | ||
| + | |||
| + | At this point <math>\left(\frac{V_{out}}{V_{in}} \right) = \frac{0.0138}{\sqrt{2}} = 0.00976</math>. Let's plot this line and calculate the bandwidth. | ||
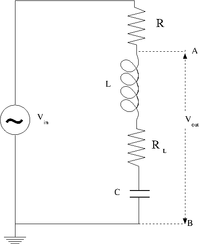
=The RLC cicuit= | =The RLC cicuit= | ||
Revision as of 23:41, 3 February 2011
- LC Resonance circuits
The LC circuit
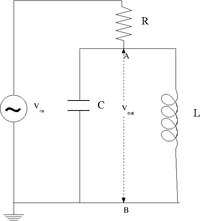
Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use = 10 - 100 , R = 1k
I choose the following values for and :
So the resonance frequency is
And
Construct the LC circuit using a non-polar capacitor
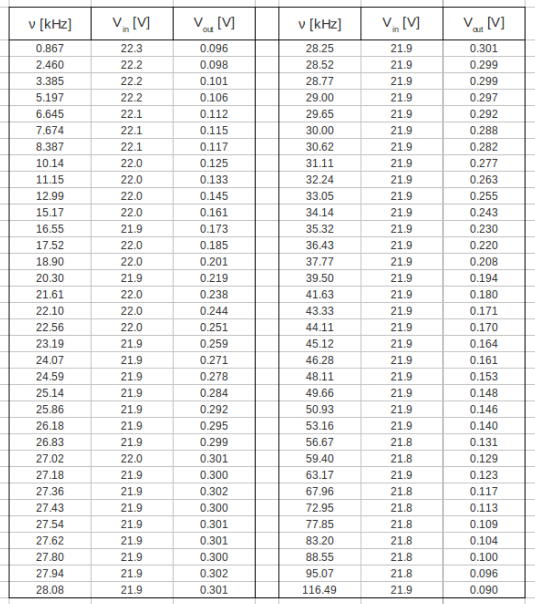
Measure the Gain as a function of frequency. (25 pnts)
Compare the measured and theoretical values of the resonance frequency () (10 pnts)
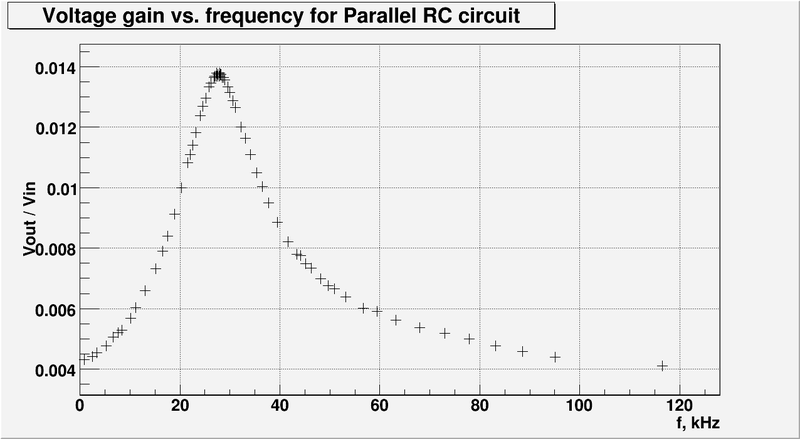
Let's plot the data from table above:
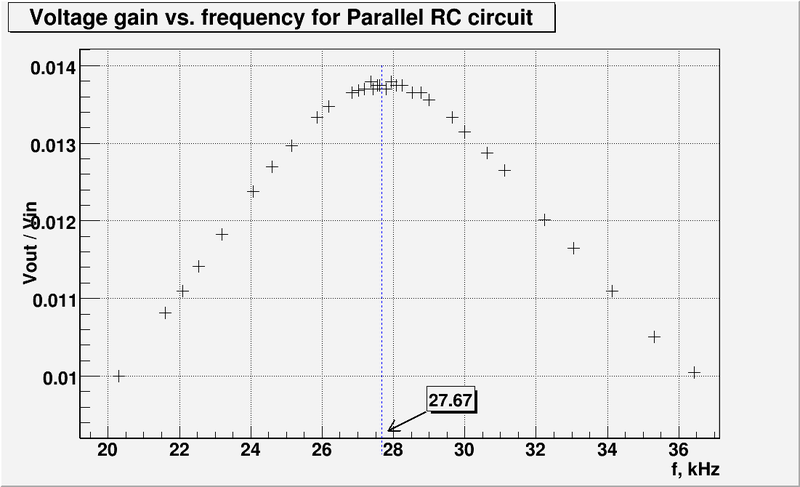
And let's zoom the graph above at resonance frequency:
So the experimentally measured resonance frequency is:
And the predicted value of resonance frequency is:
The error is:
The error is small so I was lucky
Questions
- What is the bandwidth of the above circuit? (5 pnts)
From the plot above we have
The bandwidth defined as the width from to where the amplitude of signal drop down to .
At this point . Let's plot this line and calculate the bandwidth.