Difference between revisions of "Lab 4 RS"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
= 1-50 kHz filter (20 pnts)= | = 1-50 kHz filter (20 pnts)= | ||
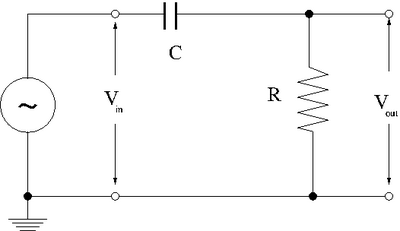
| − | 1. | + | 1. Design a high-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter's attenuation of the AC signal goes to 0(not passed). For a High pass filter, AC signals with a frequency below the 1-50 kHz range will be attenuated . |
[[File:TF_EIM_Lab4.png | 400 px]] | [[File:TF_EIM_Lab4.png | 400 px]] | ||
| Line 21: | Line 21: | ||
| − | 2. | + | 2. Now construct the circuit using a non-polar capacitor. |
| − | 3. | + | 3. Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter. |
| − | 4. | + | 4. Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz. |
{| border="3" cellpadding="20" cellspacing="0" | {| border="3" cellpadding="20" cellspacing="0" | ||
| Line 59: | Line 59: | ||
# | # | ||
| − | 5. | + | 5. Graph the <math>\log \left(\frac{V_{out}}{V_{in}} \right)</math> -vs- <math>\log (\nu)</math> |
=phase shift (10 pnts)= | =phase shift (10 pnts)= | ||
Revision as of 05:21, 26 January 2011
- RC High-pass filter
1-50 kHz filter (20 pnts)
1. Design a high-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter's attenuation of the AC signal goes to 0(not passed). For a High pass filter, AC signals with a frequency below the 1-50 kHz range will be attenuated .
- To design low-pass RC filter I had:
So
2. Now construct the circuit using a non-polar capacitor.
3. Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter.
4. Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz.
| Hz | Volts | Volts | |
5. Graph the -vs-
phase shift (10 pnts)
- measure the phase shift between and
Questions
- compare the theoretical and experimentally measured break frequencies. (5 pnts)
- Calculate and expression for as a function of , , and .(5 pnts)
- Compare the theoretical and experimental value for the phase shift . (5 pnts)
- Sketch the phasor diagram for ,, , and . Put the current along the real voltage axis. (30 pnts)
- what is the phase shift for a DC input and a very-high frequency input?(5 pnts)
- calculate and expression for the phase shift as a function of , , and graph -vs . (20 pnts)
Forest_Electronic_Instrumentation_and_Measurement
Go Back to All Lab Reports