Lab 3 RS

Go Back to All Lab Reports

RC Low-pass filter

1-50 kHz filter (20 pnts)

Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed)

To design low-pass RC filter I had:

[math]R=10.5\ \Omega[/math]  
[math]C=1.250\ \mu F[/math]

[math]\omega_b = \frac{1}{RC} = 76.2\cdot 10^3\ \frac{rad}{s}[/math]
[math]f_b = \frac{\omega_b}{2\pi} = 12.1\ \mbox{kHz}[/math]

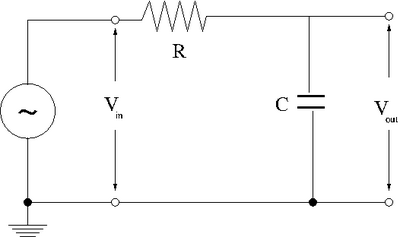
Now construct the circuit using a non-polar capacitor

Measure the input [math](V_{in})[/math] and output [math](V_{out})[/math] voltages for at least 8 different frequencies[math] (\nu)[/math] which span the frequency range from 1 Hz to 1 MHz

[math]\nu\ [\mbox{kHz}][/math]	[math]V_{in}\ [V][/math]	[math]V_{out}\ [V][/math]	[math]\frac{V_{out}}{V_{in}}[/math]	[math]\delta t\ [\mu s][/math]	[math]\phi = \omega \delta t\ [rad][/math]
0.1	5.0	5.0	1.0
1.0	4.2	4.2	1.0	14.0	0.094
2.0	3.2	3.1	0.97	14.0	0.188
5.0	1.8	1.6	0.89	14.0	0.471
10.0	1.14	0.88	0.77	11.0	0.628
16.7	0.90	0.54	0.60	8.5	1.049
20.0	0.88	0.48	0.54	8.0	1.005
25.0	0.82	0.38	0.46	7.0	1.099
33.3	0.78	0.28	0.36	6.0	1.255
50.0	0.76	0.18	0.24	4.5	1.413
100.0	0.75	0.09	0.12	2.0	1.256
125.0	0.74	0.07	0.095	1.8	1.413
200.0	0.75	0.04	0.053	0.9	1.005
333.3	0.76	0.03	0.039	0.25	0.523
200.0	0.76	0.03	0.039	-0.25	-0.785
1000.0	0.78	0.06	0.077	-0.25	-1.570

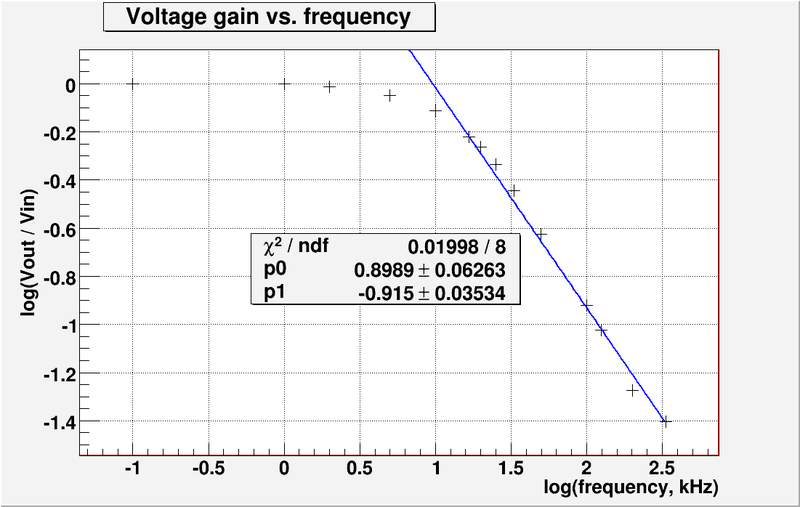
Graph the [math]\log \left(\frac{V_{out}}{V_{in}} \right)[/math] -vs- [math]\log (\nu)[/math]

phase shift (10 pnts)

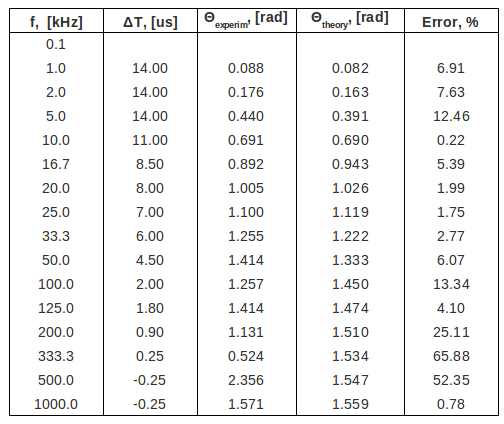
1. measure the phase shift between [math]V_{in}[/math] and [math]V_{out}[/math] as a function of frequency [math]\nu[/math]. Hint: you could use [math] V_{in}[/math] as an external trigger and measure the time until [math]V_{out}[/math] reaches a max on the scope [math](\sin(\omega t + \phi) = \sin\left ( \omega\left [t + \frac{\phi}{\omega}\right]\right )= \sin\left ( \omega\left [t + \delta t \right] \right ))[/math].

See table above, columns #5 and #6.

Questions

1. Compare the theoretical and experimentally measured break frequencies. (5 pnts)

method 1. Using fitting line

Theoretical break frequency: 12.1 kHz

Experimentally measured break frequency: 9.59 kHz

 Q: The above was read off the graph?  Why not use fit results?
 A: The fit was made by using GIMP Image Editor. I do not have so much experience with ROOT. But I will try to do it. Thank you for comment.
 A1: The fit was done by ROOT

The fit line equation from the plot above is [math]\ y=0.8989-0.915\cdot x[/math].

From intersection point of line with x-axis we find:

[math]log(f_{exp})=\frac{0.8989}{0.915} = 0.982[/math]

[math]f_{exp} = 10^{0.982} = 9.59\ kHz [/math]

The error is:

[math]Error = \left| \frac{f_{exp} - f_{theor}}{f_{theor}} \right| = \left| \frac{9.59 - 12.1}{12.1} \right|= 20.7\ %[/math]

method 2. Using the -3 dB point

At the break point the voltage gain is down by 3 dB relative to the gain of unity at zero frequency. So the value of [math]\mbox{log}(V_{out}/V_{in}) = (3/20) = 0.15 [/math]. Using this value I found from plot above [math]\mbox{log}(f_b) = 1.1\ \mbox{kHz}[/math]. So [math]f_b = (10^{1.1}) = 12.6\ \mbox{kHz}[/math]. The error in this case is 4.1 %.

2. Calculate and expression for [math]\frac{V_{out}}{ V_{in}}[/math] as a function of [math]\nu[/math], [math]R[/math], and [math]C[/math]. The Gain is defined as the ratio of [math]V_{out}[/math] to [math]V_{in}[/math].(5 pnts)

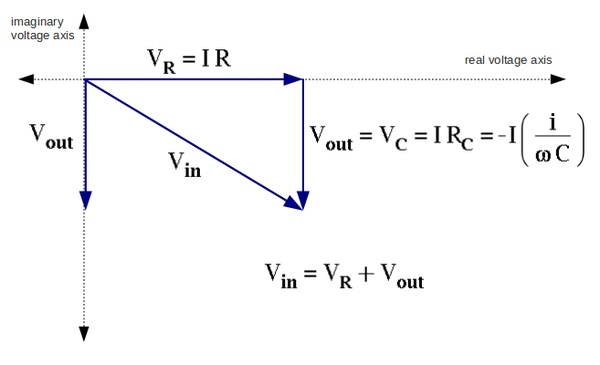
We have:

[math]1)\ V_{in} = I\left(R+R_C\right) = I\left(R+\frac{1}{i\omega C}\right)[/math]

[math]2)\ V_{out} = I \left(\frac{1}{i\omega C}\right) [/math]

Dividing second equation into first one we get the voltage gain:

[math]\ \frac{V_{out}}{V_{in}} = \frac{I \left(\frac{1}{i\omega C}\right)}{I\left(R+\frac{1}{i\omega C}\right)} = \frac{\left(\frac{1}{i\omega C}\right)}{\left(R+\frac{1}{i\omega C}\right)} = \frac{1}{1+i\omega RC}[/math]

And we are need the real part:

[math]\left |\frac{V_{out}}{V_{in}} \right | = \sqrt{ \left( \frac{V_{out}}{V_{in}} \right)^* \left( \frac{V_{out}}{V_{in}} \right)} = \sqrt{\left ( \frac{1}{1+i\omega RC}\right ) \left ( \frac{1}{1-i\omega RC}\right )} = \frac{1}{\sqrt{(1 + (\omega RC)^2}} = \frac{1}{\sqrt{(1 + (2\pi \nu RC)^2}}[/math]

3. Sketch the phasor diagram for [math]V_{in}[/math],[math] V_{out}[/math], [math]V_{R}[/math], and [math]V_{C}[/math]. Put the current [math]I[/math] along the real voltage axis. (30 pnts)

4. Compare the theoretical and experimental value for the phase shift [math]\theta[/math]. (5 pnts)

The experimental phase shift is [math]\ \Theta_{exper} = (\omega\ \delta T)_{exper}[/math]

The theoretical phase shift is [math]\ \Theta_{theory}=\mbox{arctan}(\omega RC)[/math]

6. calculate and expression for the phase shift [math]\theta[/math] as a function of [math]\nu[/math], [math]R[/math], [math]C[/math] and graph [math]\theta[/math] -vs [math]\nu[/math]. (20 pnts)

Forest_Electronic_Instrumentation_and_Measurement

Go Back to All Lab Reports