Qweak Qsqrd Tracking

Tracking system Description

The Qweak tracking system is composed of three tracking regions. Region 1 is a GEM based ionization chamber which measures the radial distance of a hit from the beam pipe center and is located 50 cm away from a 20 cm long target. Region 2 is a drift chamber with 6 layers located 1.5 m from target center. A Torous magnet is place centered 2 meters from the target which selects elasticly scattered electrons that pass through a primary collimator just before the magnet. Region 2 is another drift chamber located just in front of the quartz cherenkov detectors. A scintillator appears after the quartz cherenkov detector which is used to trigger the tracking system.

[math]Q^2[/math] for Elastic Scattering

General Expression for [math]Q^2[/math] Elastic scattering error

[math]\lt \delta Q\gt ^2 = \left ( \frac{\partial Q}{\partial E} \right )^2 \left( \delta E \right )^2 + \left ( \frac{\partial Q}{\partial \theta} \right )^2 \left( \delta \theta \right )^2 + \left ( \frac{\partial Q}{\partial \theta \partial E} \right )^2 \left( \delta \theta \delta E \right )[/math]

= [math]\frac{16 E_i^2 M_p^2 \sin^2(\theta/2)}{(E_i +M_p - E_i \cos(\theta))^6} [/math]

[math]\times \left [ \left ( 4 M_p^4 \sin^2(\theta/2) + 24 E_i M_p^3 \sin^4(\theta/2) + 52 E_i^2M_p^2 \sin^6(\theta/2) + 48 E_i^3 M_p \sin^8(\theta/2) + 16 E_i^4 \sin^{10}(\theta/2) \right )(\delta E)^2 +4M_p^2 \cos^2(\theta/2) \left ( \delta E \delta \theta\right )^2\right ][/math]

[math]+\left { E_i^2 \right}\cos^2(\theta/2)\left ( \delta \theta \right)^2[/math]

Error using only R1

This simple calculation assumes that only the electron distance from the beamline measured 0.5 m from the target center by the GEM detector will be used to calculate [math]\theta[/math].

[math]\tan(\theta) = \frac{r \sin(\theta)}{r \cos(\theta)} = \frac{d}{Z} [/math]

assuming the error is[math] \delta d = 100 \mu m[/math] and [math]\delta Z = 30 cm[/math] = length of the target

[math]\frac{\delta \tan(\theta)}{\theta} = \sqrt{\left( \frac{\delta d }{d} \right )^2+ \left( \frac{\delta Z }{Z} \right )^2}[/math]

If Z = 0.5 m and d = 15 cm

then

[math]\frac{\delta \tan(\theta)}{\theta}= 0.6[/math]

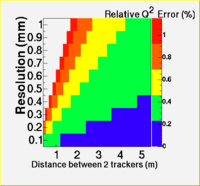
Using only R1 and R2

R1 and R2 together may be used to reconstruct straight tracks and determine the [math]Q^2[/math] of elasticly scattered electrons. The [math]Q^2[/math] for elastically scattered electrons can be determine if the incident electron energy (E) and the scattered electron zenith angle [math](\theta)[/math] are known where the "z-axis" of a spherical coordinate system is directed down the beam pipe in the direction of the incident electron. The Region 1 tracking system measures the distance of the scattered electron from the center of the beam pipe [math](r \sin(\theta))[/math]. For a point target one would be able to determine the scattering angle \theta using the distance of the Region 1 detector from the target. The Qweak target, however is extended in the "z" direction and prevents an accurate calculation of [math]\theta[/math] with just one tracking element. A second tracking element, Region 2, along with knowledge of the "X" and "Y" location of the incident beam will enable a determination of a plane intersecting the z-axis at the interaction point. The scattering angle [math]\theta[/math] can be determined using

[math]\tan(\theta) = \frac{r \sin(\theta)}{r \cos(\theta)} = \frac{r \sin(\theta)}{Z} [/math]

or

[math]\theta = \tan^{-1}\left ( \frac{r \sin(\theta)}{Z}\right )[/math]

A plot of the [math]Q^2[/math] error achievable by 2 tracking systems according to the distance Z between the systems and their combined tracking resolution in mm.

File:QsqrdErr.c