Difference between revisions of "Large Deflection Membrane Stiffened Static Analysis"
| Line 29: | Line 29: | ||
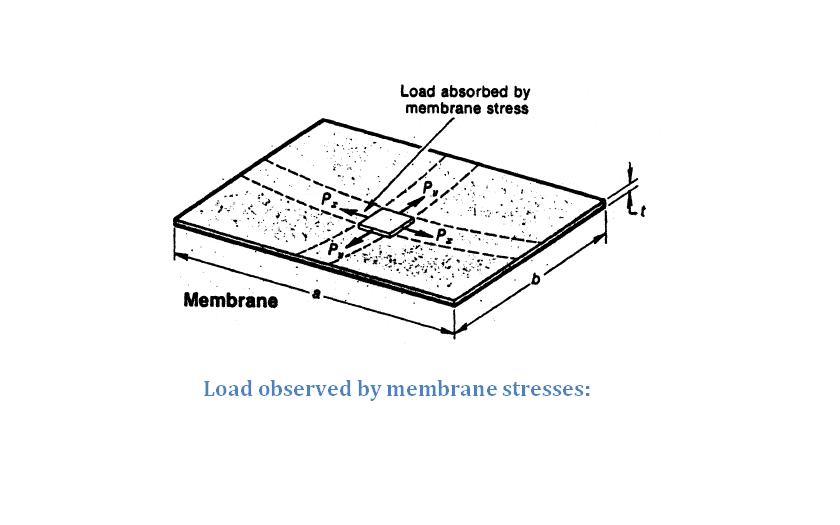
===Load observed by membrane stresses=== | ===Load observed by membrane stresses=== | ||
Load is always applied along the membrane. This is usually a 2D case. Both the Load and deformation will be in the same plane along the membrane | Load is always applied along the membrane. This is usually a 2D case. Both the Load and deformation will be in the same plane along the membrane | ||
| − | + | [[Image:Eldmssa6.jpg]] | |
===Load observed by both bending and membrane stresses=== | ===Load observed by both bending and membrane stresses=== | ||
Revision as of 12:22, 9 June 2008
As the thickness is quite small i.e. 0.254mm and the young’s modulus being 3800Mpa, the sheet behaves very week and will exhibit extreme deflections as per the small displacement theory, so a non-linear and high deformation case will give better and realistic results.
Small displacement theory assumes that deflections will not be large enough for this to happen. With the small deflection assumption, the initial stiffness with the structure in the un-deformed position is assumed to be valid for the whole analysis. In essence the linear analysis simply works with the bending moment of inertia and transverse shear stiffness of the plate and uses that to calculate the deflections. Since the thickness is so small, the moment of inertia is very small, so it calculates a large displacement. In reality what happens is that as pressure is applied to the panel, it immediately deflects and then starts pulling on the plate edges and carrying the load in tension. This is called membrane stiffening. An ideal membrane has absolutely no bending stiffness and carries all loading by this stretching effect. As the thickness is quite small i.e. 0.254mm and the young’s modulus being 3800Mpa, the sheet behaves very week and will exhibit extreme deflections as per the small displacement theory, so a non-linear and high deformation case established with membrane stiffening will give better and realistic results.
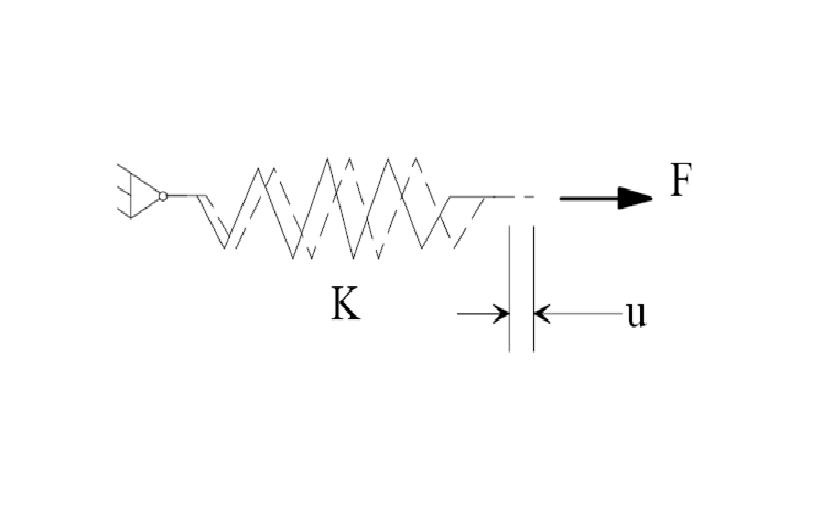
The basic equation of the finite element method is [K]{U} = {F}, where [K] is the stiffness, {U} is the displacement vector, and {F} is the applied load vector. This is analogous to a simple spring, and is the essence of “small deflection theory”.
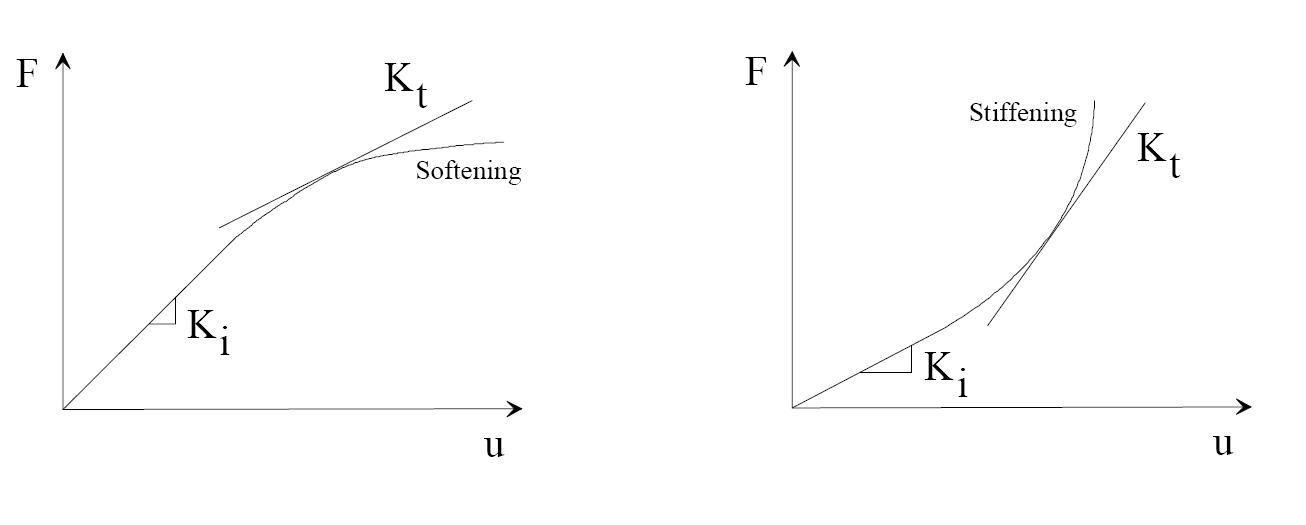
For some structures however, this relationship between force and displacement is not constant, because as the structure deflects, the stiffness changes. This occurs due to the geometric linearity. Geometric nonlinearity is a situation where the displacement does not have a straight-line response to the applied loads. It also has very large displacements and rotations.
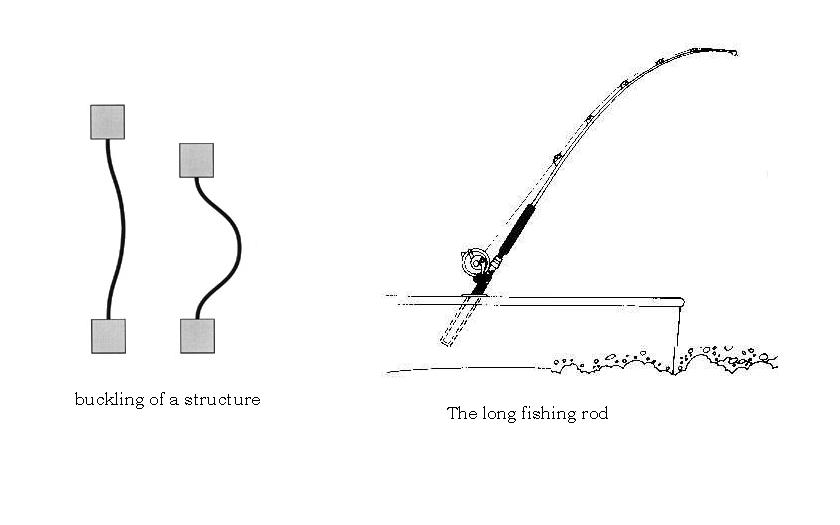
An example of stress softening could be the buckling of a structure. As it gets closer and closer to the buckling point, there is more and more deflection for steadily increasing applied load, until at the buckling or collapsing load the deflection is extreme for a very small increase in load.
The long fishing rod is an example of stress stiffening. There is less and less deflection as the load increases because the orientation of the applied load has changed with respect to the tip and also has moved closer to the end where you are holding it, reducing the bending moment.
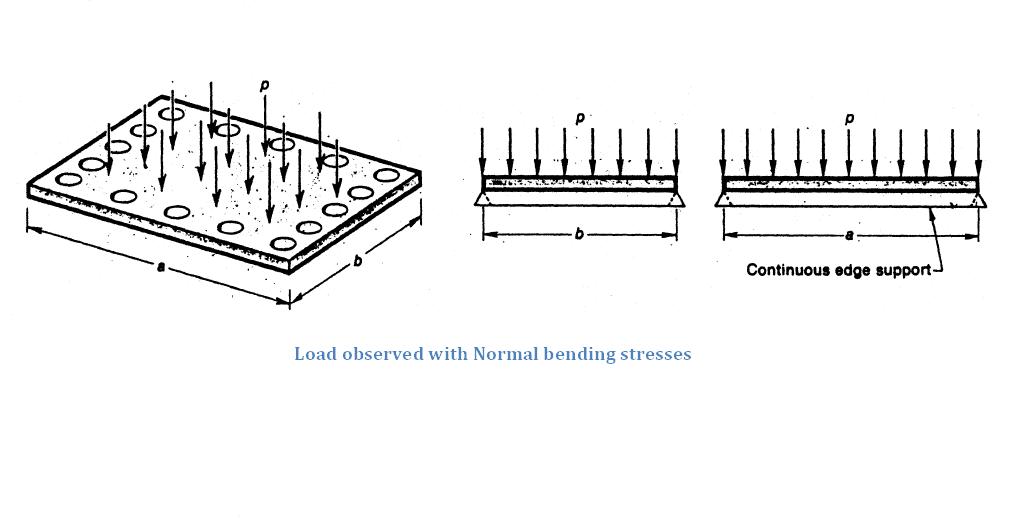
Load observed with Normal bending stresses
The load applied will always be perpendicular to the plate. These cases are considered when the deflection is not more than half of the thickness of the plate File:Eldmssa4.jpg
Load observed by membrane stresses
Load is always applied along the membrane. This is usually a 2D case. Both the Load and deformation will be in the same plane along the membrane
Load observed by both bending and membrane stresses
This case occurs when the loading is along the normal and the membrane.
The pressure on the Mylar sheet will be perpendicular to the plane at the beginning. However, as the deformation starts to occur, the material will be stretched in such a way that membrane is pulled into the direction of load and now the normal pressure becomes membrane load. So, now the membrane stiffened static analysis with large deflection can be carried out on the same square and circular shapes.