Difference between revisions of "Monte Carlo Binary Collision Approximation"
| Line 10: | Line 10: | ||
Nuclear fission of uranium-235 yields an enormous amount of energy from the fact that the fission products have less total mass than the uranium nucleus, a mass change that is converted to energy by the Einstein relationship <math>E=mc^2</math>. Using the Law of Conservation of Energy, we can look at the total energy before and after the fission to determine how much energy is released in this process. | Nuclear fission of uranium-235 yields an enormous amount of energy from the fact that the fission products have less total mass than the uranium nucleus, a mass change that is converted to energy by the Einstein relationship <math>E=mc^2</math>. Using the Law of Conservation of Energy, we can look at the total energy before and after the fission to determine how much energy is released in this process. | ||
| − | <center><math>^{236}_{92}U : 92(938.272\ MeV)+144(939.565\ MeV)\ =\ 221. | + | <center><math>^{236}_{92}U : 92(938.272\ MeV)+144(939.565\ MeV)\ =\ 221.678\ GeV</math></center> |
<center><math>^{140}_{54}Xe : 54(938.272\ MeV)+86(939.565\ MeV)\ =\ 131.469\ GeV</math></center> | <center><math>^{140}_{54}Xe : 54(938.272\ MeV)+86(939.565\ MeV)\ =\ 131.469\ GeV</math></center> | ||
<center><math>^{94}_{38}Sr : 38(938.272\ MeV)+56(939.565\ MeV)\ =\ 88.269\ GeV</math></center> | <center><math>^{94}_{38}Sr : 38(938.272\ MeV)+56(939.565\ MeV)\ =\ 88.269\ GeV</math></center> | ||
| − | <center><math> | + | <center><math>3*n : 2(939.565\ MeV)\ =\ 1.879\ GeV</math></center> |
<center><math>-----------------------------</math></center> | <center><math>-----------------------------</math></center> | ||
| − | <center><math> Energy released= | + | <center><math> Energy released=341\ MeV</math></center> |
| + | |||
| + | |||
| + | The discrepancy in energy comes from the binding energy holding he nuclei together in the Uranium. When this energy is released, it often is primarily in the form of kinetic energy of the fission fragments. When the heavier element, in this case the Xenon, travels at a high velocity due to it's large kinetic energy through material, irradiation damage occurs. | ||
| + | |||
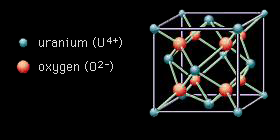
| + | The Binary Collision Approximation is a method of determining irradiated damage to material by simply looking at one collision of the fission fragment per atom a time. Since a common nuclear material is Uranium Oxide, <math>UO_2</math> we can simulate damage in this material by estimating it has a crystalline lattice structure. This method allows to account for the binding energies needed to remove or displace atoms from their stationary positions. | ||
| + | |||
| + | |||
| + | |||
| + | <center>[[File:UO2.png|"thumb"|"border"|"center"|"middle"|"upright"|||page=Page||Figure 2: An Uranium Oxide lattice structure. ]]</center> | ||
| + | |||
| + | As the Xenon atom travels through the Uranium Oxide, Uranium and Oxygen atoms are removed from their stationary positions. These atoms can either end up in new positions within the material that were not originally positions held by atoms or replace previously knocked out atoms. These two conditions, referred to as interstitial and replacements are the two possibilities for the atoms after irradiation damage. The original atom positions can also remain empty, creating what are termed vacancies within the lattice. All three conditions are the main descriptions of how materials are damaged by atoms after such an event. My work has focused on building a new model using GEANT4 to update and improve on previous methods used to perform a Binary Collision Approximation. | ||
| + | |||
| + | |||
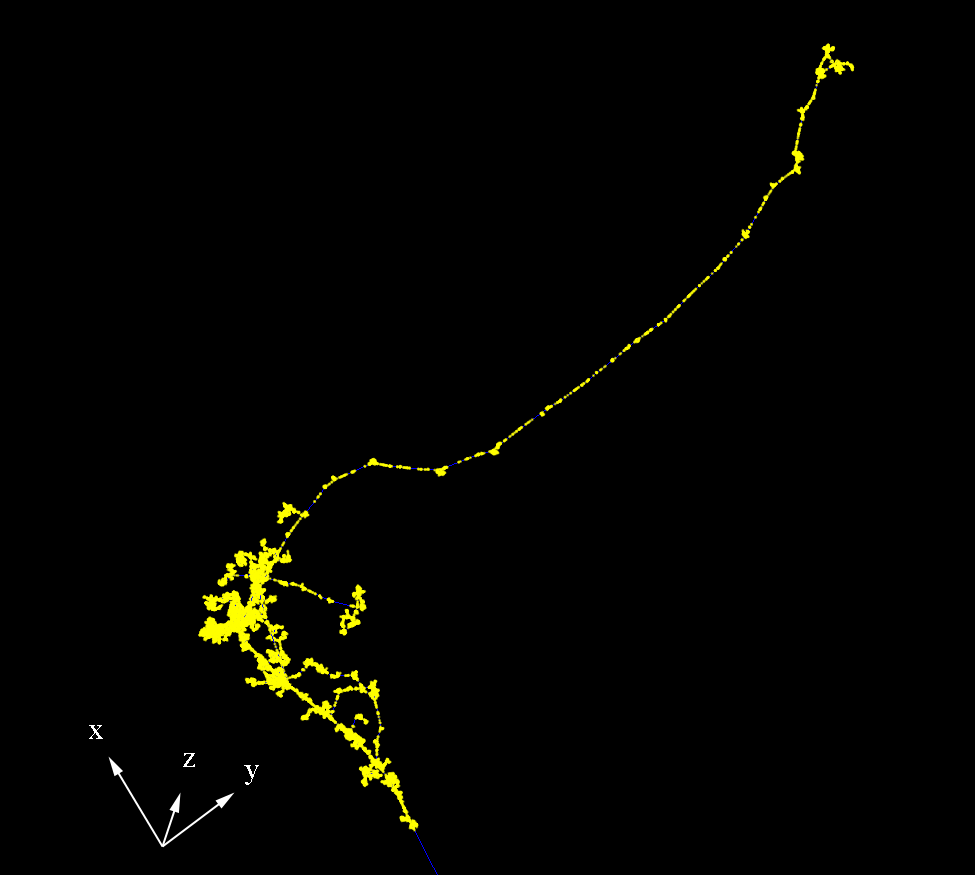
| + | <center>[[File:Damage.png|"thumb"|"border"|"center"|"middle"|"upright"|||page=Page||Figure 3: A typical damage shower within Uranium Oxide. The blue track near the bottom is the initial entrance of the Xenon within the material. The yellow dots are sites where lattices are located after collision between atoms occur. The initial energy of the Xenon was 100MeV, which typically results in around 200,000 or more vacancies. ]]</center> | ||
Revision as of 04:22, 26 February 2019
When uranium-235 undergoes fission, the average of the fragment mass is about 118, but it is more probable that the pair will have an unequal distribution in mass. A common pair of fragments from uranium-235 fission is xenon and strontium as shown in the reaction:
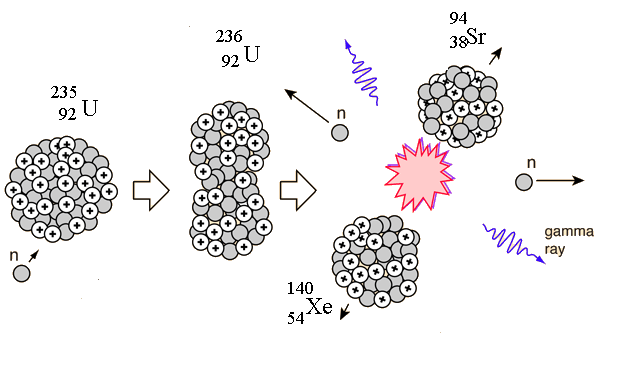
Nuclear fission of uranium-235 yields an enormous amount of energy from the fact that the fission products have less total mass than the uranium nucleus, a mass change that is converted to energy by the Einstein relationship . Using the Law of Conservation of Energy, we can look at the total energy before and after the fission to determine how much energy is released in this process.
The discrepancy in energy comes from the binding energy holding he nuclei together in the Uranium. When this energy is released, it often is primarily in the form of kinetic energy of the fission fragments. When the heavier element, in this case the Xenon, travels at a high velocity due to it's large kinetic energy through material, irradiation damage occurs.
The Binary Collision Approximation is a method of determining irradiated damage to material by simply looking at one collision of the fission fragment per atom a time. Since a common nuclear material is Uranium Oxide, we can simulate damage in this material by estimating it has a crystalline lattice structure. This method allows to account for the binding energies needed to remove or displace atoms from their stationary positions.
As the Xenon atom travels through the Uranium Oxide, Uranium and Oxygen atoms are removed from their stationary positions. These atoms can either end up in new positions within the material that were not originally positions held by atoms or replace previously knocked out atoms. These two conditions, referred to as interstitial and replacements are the two possibilities for the atoms after irradiation damage. The original atom positions can also remain empty, creating what are termed vacancies within the lattice. All three conditions are the main descriptions of how materials are damaged by atoms after such an event. My work has focused on building a new model using GEANT4 to update and improve on previous methods used to perform a Binary Collision Approximation.