Difference between revisions of "Monte Carlo Binary Collision Approximation"
Jump to navigation
Jump to search
<math> Energy released=
| Line 10: | Line 10: | ||
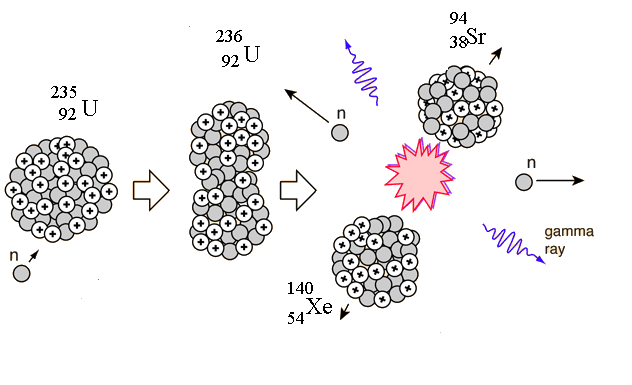
Nuclear fission of uranium-235 yields an enormous amount of energy from the fact that the fission products have less total mass than the uranium nucleus, a mass change that is converted to energy by the Einstein relationship <math>E=mc^2</math>. Using the Law of Conservation of Energy, we can look at the total energy before and after the fission to determine how much energy is released in this process. | Nuclear fission of uranium-235 yields an enormous amount of energy from the fact that the fission products have less total mass than the uranium nucleus, a mass change that is converted to energy by the Einstein relationship <math>E=mc^2</math>. Using the Law of Conservation of Energy, we can look at the total energy before and after the fission to determine how much energy is released in this process. | ||
| − | <center><math>^{ | + | <center><math>^{236}_{92}U : 92(938.272\ MeV)+144(939.565\ MeV)\ =\ 221.618\ GeV</math></center> |
| − | <center><math>^{140}_{54}Xe : 54(938.272\ MeV)+86(939.565\ MeV)\ =\ \ GeV</math></center> | + | <center><math>^{140}_{54}Xe : 54(938.272\ MeV)+86(939.565\ MeV)\ =\ 131.469\ GeV</math></center> |
| − | <center><math>^{94}_{38}Sr : 38(938.272\ MeV)+56(939.565\ MeV)\ =\ \ GeV</math></center> | + | <center><math>^{94}_{38}Sr : 38(938.272\ MeV)+56(939.565\ MeV)\ =\ 88.269\ GeV</math></center> |
| − | <center><math>2*n : 2(939.565\ MeV)\ =\ 1.879\ GeV</center> | + | <center><math>2*n : 2(939.565\ MeV)\ =\ 1.879\ GeV</math></center> |
<center><math>-----------------------------</math></center> | <center><math>-----------------------------</math></center> | ||
<center><math> Energy released= | <center><math> Energy released= | ||
Revision as of 03:45, 26 February 2019
When uranium-235 undergoes fission, the average of the fragment mass is about 118, but it is more probable that the pair will have an unequal distribution in mass. A common pair of fragments from uranium-235 fission is xenon and strontium as shown in the reaction:

Nuclear fission of uranium-235 yields an enormous amount of energy from the fact that the fission products have less total mass than the uranium nucleus, a mass change that is converted to energy by the Einstein relationship . Using the Law of Conservation of Energy, we can look at the total energy before and after the fission to determine how much energy is released in this process.