Difference between revisions of "Linac Run Plan April 2018, Dr. McNulty"
| Line 153: | Line 153: | ||
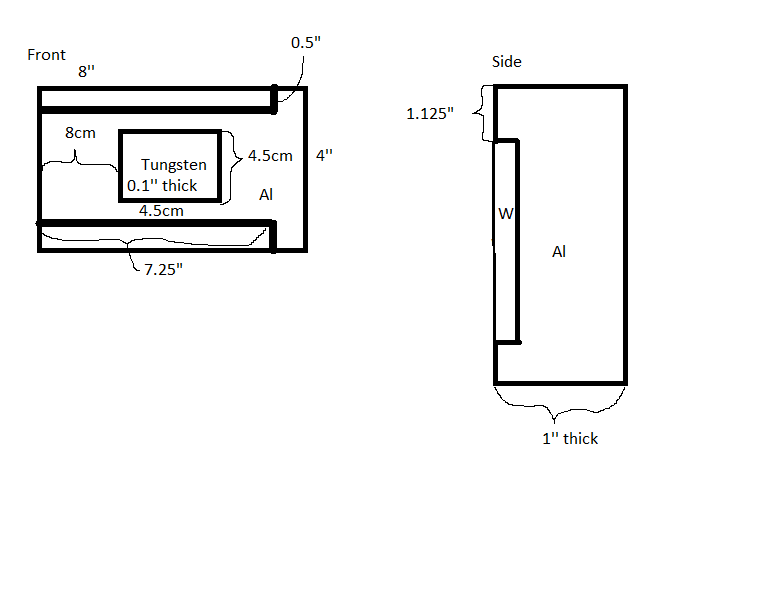
Added .254cm of Tungsten and 2.286cm of Aluminum to be used as converter and beam stop. | Added .254cm of Tungsten and 2.286cm of Aluminum to be used as converter and beam stop. | ||
| − | [[ | + | [[File:Radiator.png]] |
Assuming <math>25\frac{mA}{pulse}</math> and a pulse width of <math>100ns</math> | Assuming <math>25\frac{mA}{pulse}</math> and a pulse width of <math>100ns</math> | ||
Revision as of 21:59, 24 April 2018
Absorbed Dose Information
100mA, 100ns pulse width, 25cm from beam pipe
Assuming and a pulse width of
Then
Using a distance of 25cm for all simulations following.
OSL
of a pulse. ~62mil e- simulated, ~62bil e- per pulse. With beam parameters given above.
Deposited Energy:
OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.
OSL Crystal density
Mass of a single OSL crystal:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse
Quartz
of a pulse. ~62mil e- simulated, ~62bil e- per pulse. With beam parameters given above.
Deposited Energy:
Quartz Geometry: 1 inch cylinder with electrons incident upon the base of the cylinder.
Quartz density
Mass of Quartz used in simulation:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse
25mA, 100ns pulse width, 25cm from beam pipe
Cut current by a factor of 4. 100mA->25mA
Assuming and a pulse width of
Then
Using a distance of 25cm for all simulations following.
OSL
of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
Deposited Energy:
OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.
OSL Crystal density
Mass of a single OSL crystal:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse
Quartz
of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
Deposited Energy:
Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.
Quartz density
Mass of Quartz used in simulation:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse
25mA, 100ns pulse width, 50cm from beam pipe
Changed distance from end of beam pipe from 25cm to 50cm.
Cut current by a factor of 4. 100mA->25mA
Assuming and a pulse width of
Then
OSL
of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
Deposited Energy:
OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.
OSL Crystal density
Mass of a single OSL crystal:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse:
Quartz
of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
Deposited Energy:
Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.
Quartz density
Mass of Quartz used in simulation:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse
25mA, 100ns pulse width, 50cm from beam pipe, tungsten target with aluminum beamstop
Added .254cm of Tungsten and 2.286cm of Aluminum to be used as converter and beam stop.
Assuming and a pulse width of
Then
OSL
of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
Deposited Energy:
OSL geometry: 0.501cm diameter cylinder of 0.03cm thickness with beam incident on flat face.
OSL Crystal density
Mass of a single OSL crystal:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse:
Quartz
of a pulse. ~15mil e- simulated, ~15bil e- per pulse. With beam parameters given above.
Deposited Energy:
Quartz Geometry: 1 inch diameter, 0.5 inch tall cylinder with electrons incident upon the base of the cylinder.
Quartz density
Mass of Quartz used in simulation:
Scaling deposited energy by 1000 to account for only shooting a 1000th of a pulse, the deposited energy becomes
Converting to Joules for dose calculation:
Average dose per pulse