Scattering Amplitude

Scattering Amplitude

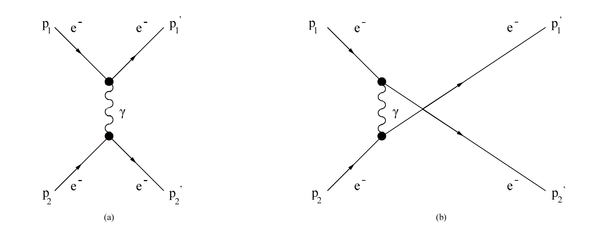
In the Møller scattering [math](\mathbf P_1 + \mathbf P_2 \rightarrow \mathbf P_1^' + \mathbf P_2^')[/math] we have deal with identical particles in the initial and final states, which means that the amplitude has to be symmetric under interchange of particles [math](\mathbf P_1^' \leftrightarrow \mathbf P_2^' [/math] or [math] \mathbf P_1 \leftrightarrow \mathbf P_2)[/math]. As a consequence there will be two Feynman diagrams to describe this scattering.

[math]\mathfrak{M}=\mathfrak{M}_1+\mathfrak{M}_2[/math]

Using the Feynman rules, each vertex contribute a factor

[math]ie(\mathbf p_{initial} + \mathbf p_{final})^{\mu}[/math]

and the propagator gives

[math] \frac{−ig_{\mu \nu}}{q^2}[/math]

where q is the momentum of the photon

[math]q \equiv \mathbf p_{final}-\mathbf p_{initial}[/math]

[math]-i \mathfrak{M}_1=ie(\mathbf p_1+\mathbf p_1^')^{\mu} \left (\frac{-ig_{\mu \nu}}{q^2} \right ) ie ( \mathbf p_{2}+\mathbf p_2^')^{\nu} \qquad \qquad -i \mathfrak{M}_2=ie(\mathbf p_1+\mathbf p_2^')^{\mu} \left (\frac{-ig_{\mu \nu}}{q^2} \right ) ie ( \mathbf p_{2}+\mathbf p_1^')^{\nu}[/math]

[math]-i \mathfrak{M}_1=ie(\mathbf p_1+\mathbf p_1^')^{\mu} \left (\frac{-ig_{\mu \nu}}{(\mathbf p_2^'-\mathbf p_2)^2} \right ) ie( \mathbf p_{2}+\mathbf p_2^')^{\nu} \qquad \qquad -i \mathfrak{M}_2=ie(\mathbf p_1+\mathbf p_2^')^{\mu} \left (\frac{-ig_{\mu \nu}}{(\mathbf p_1^'-\mathbf p_2)^2} \right ) ie( \mathbf p_{2}+\mathbf p_1^')^{\nu}[/math]

[math]-i \mathfrak{M}_1=ie^2\left (\frac{(\mathbf p_1+\mathbf p_1^')_{\mu} (\mathbf p_{2}+\mathbf p_2^')^{\mu}}{(\mathbf p_2^'-\mathbf p_2)^2} \right ) \qquad \qquad -i \mathfrak{M}_2=ie^2\left (\frac{(\mathbf p_1+\mathbf p_2^')_{\mu} (\mathbf p_{2}+\mathbf p_1^')^{\mu}}{(\mathbf p_1^'-\mathbf p_2)^2} \right ) [/math]

Without loss of generality, we can extend this to the center of mass frame

[math]-i \mathfrak{M}_{e^-e^-}=-ie^2 \left ( \frac{(\mathbf p_1^*+\mathbf p_{1}^{'*})_{\mu}(\mathbf p_2^*+\mathbf p_{2}^{'*})^{\mu}}{(\mathbf p_{2}^{'*}-\mathbf p_2^*)^2}- \frac{(\mathbf p_1^*+\mathbf p_{2}^{'*})_{\mu}(\mathbf p_2^*+\mathbf p_{1}^{'*})^{\mu}}{(\mathbf p_{1}^{'*}-\mathbf p_2^*)^2} \right )[/math]

[math] \mathfrak{M}_{e^-e^-}= e^2\left ( \frac{\mathbf P_1^* \mathbf P_2^*+\mathbf P_{1}^{'*} \mathbf P_{2}^{'*}+\mathbf P_{1}^{'*} \mathbf P_2^*+\mathbf P_1^* \mathbf P_{2}^{'*}}{(\mathbf P_{2}^{'*}-\mathbf P_2^*)^2}- \frac{\mathbf P_1^* \mathbf P_2^*+\mathbf P_{2}^{'*} \mathbf P_{1}^{'*}+\mathbf P_{2}^{'*} \mathbf P_2^*+\mathbf P_1^* \mathbf P_{1}^*}{(\mathbf P_{1}^{'*}-\mathbf P_2^*)^2} \right )[/math]

Using the fact that [math]\mathbf P_1^{'*} \mathbf P_2^{'*}=\mathbf P_1^* \mathbf P_2^* \quad \quad \mathbf P_1^{'*} \mathbf P_1^{*}=\mathbf P_2^{'*} \mathbf P_2^* \quad \quad \mathbf P_1^{*} \mathbf P_2^{'*}=\mathbf P_2^* \mathbf P_1^{'*}[/math]

[math] \mathfrak{M}_{e^-e^-}= e^2\left ( \frac{2\mathbf P_1^* \mathbf P_2^*+2\mathbf P_{1}^{'*} \mathbf P_2^*}{(\mathbf P_{2}^{'*2}-2\mathbf P_{2}^{'*}\mathbf P_2^{*}+\mathbf P_2^{*2})}- \frac{2\mathbf P_1^* \mathbf P_2^*+2\mathbf P_1^* \mathbf P_{1}^{'*}}{(\mathbf P_{1}^{'*2}-2\mathbf P_{1}^{'*}\mathbf P_2^{'*}+\mathbf P_2^{'*2})} \right )[/math]

[math] \mathfrak{M}_{e^-e^-}= e^2\left ( \frac{2\mathbf P_1^* \mathbf P_2^*+2\mathbf P_{1}^{'*} \mathbf P_2^*}{(\mathbf P_2^{*2}-2\mathbf P_2^{*}\mathbf P_{2}^{'*}+\mathbf P_{2}^{'*2})}- \frac{2\mathbf P_1^* \mathbf P_2^*+2\mathbf P_1^* \mathbf P_{1}^{'*}}{(\mathbf P_2^{'*2}-2\mathbf P_2^{'*}\mathbf P_{1}^{'*}+\mathbf P_{1}^{'*2})} \right )[/math]

[math] \mathfrak{M}_{e^-e^-}= e^2\left ( \frac{2\mathbf P_1^* \mathbf P_2^*+2\mathbf P_{1}^{'*} \mathbf P_2^*}{(\mathbf P_2^*-\mathbf P_{2}^{'*})^2}- \frac{2\mathbf P_1^* \mathbf P_2^*+2\mathbf P_1^* \mathbf P_{1}^{'*}}{(\mathbf P_2^{'*}-\mathbf P_{1}^{'*})^2} \right )[/math]

[math] \mathfrak{M}_{e^-e^-}= e^2\left ( \frac{ (\mathbf P_1^{*2}-2 \mathbf P_1^* \mathbf P_2^{'*}+ \mathbf P_2^{'*2})-(\mathbf P_1^{*2}+2 \mathbf P_1^* \mathbf P_2^*+ \mathbf P_2^{*2})}{t}- \frac{(\mathbf P_1^{*2}-2 \mathbf P_1^* \mathbf P_1^{'*}+ \mathbf P_1^{'*2})-( \mathbf P_1^{*2}+2 \mathbf P_1^* \mathbf P_2^*+ \mathbf P_2^{*2})}{u} \right )[/math]

[math]\mathfrak{M}_{e^-e^-}=e^2 \left (\frac{u-s}{t}+\frac{t-s}{u} \right )[/math]