Difference between revisions of "Mandelstam Representation"
Jump to navigation
Jump to search
| Line 23: | Line 23: | ||
<center><math>\Longrightarrow \left({\mathbf P_1^*}- {\mathbf P_2^{'*}}\right)^2=\left({\mathbf P_2^*}- {\mathbf P_1^{'*}}\right)^2\equiv u</math></center> | <center><math>\Longrightarrow \left({\mathbf P_1^*}- {\mathbf P_2^{'*}}\right)^2=\left({\mathbf P_2^*}- {\mathbf P_1^{'*}}\right)^2\equiv u</math></center> | ||
| + | |||
| + | |||
| + | ==s Channel== | ||
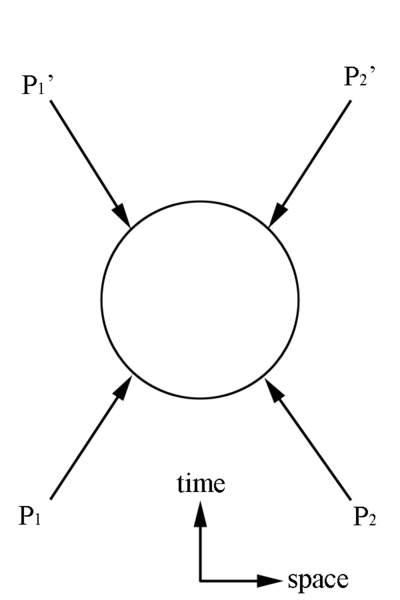
The s quantity is known as the square of the center of mass energy (invariant mass) | The s quantity is known as the square of the center of mass energy (invariant mass) | ||
| + | <center><math>s \equiv \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=\left({\mathbf P_1^{'*}}+ {\mathbf P_2^{'*}}\right)^2</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><math>s \equiv \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2</math></center> | ||
| + | |||
| + | |||
| + | <center><math>s \equiv \mathbf P_1^{*2}+2 \mathbf P_1^* \mathbf P_2^*+ \mathbf P_2^{*2}</math></center> | ||
| + | |||
| + | |||
| + | As shown earlier, the square of a 4-momentum is | ||
| + | |||
| + | |||
| + | <center><math>\mathbf P^{2} \equiv m^2</math></center> | ||
| + | |||
| + | |||
| + | <center><math>s \equiv m^{2}+2 \mathbf P_1^* \mathbf P_2^*+ m_2^{2}</math></center> | ||
| + | |||
| + | |||
| + | This gives | ||
| + | |||
| + | <center><math>s \equiv 2m^{2}+2 \mathbf P_1^* \mathbf P_2^*</math></center> | ||
| + | |||
| + | |||
| + | Similarly, the scalar product of two 4-momentums | ||
| + | |||
| + | <center><math>s \equiv 2m^2+2(E_1^*E_2^*-\vec p_1^* \vec p_2^*)</math></center> | ||
| + | |||
| + | |||
| + | In the center of mass frame of reference, | ||
| + | |||
| + | <center><math>E_1^*=E_2^* \quad and \quad \vec p_1^*=-\vec p_2^*</math></center> | ||
| + | |||
| + | |||
| + | <center><math>s \equiv 2m^2+2(E_1^{*2}+\vec p_1^{*2} )</math></center> | ||
| + | |||
| + | Using the relativistic energy equation | ||
| + | <center><math>E^2 \equiv p^2+m^2</math></center> | ||
| + | |||
| + | |||
| + | <center><math>s \equiv 2m^2+2((m^2+p_1^{*2})+p_1^{*2})</math></center> | ||
| + | |||
| + | |||
| + | <center><math>s=4(m_{CM}^2+p_{CM}^2)</math></center> | ||
| + | |||
| + | ==t Channel== | ||
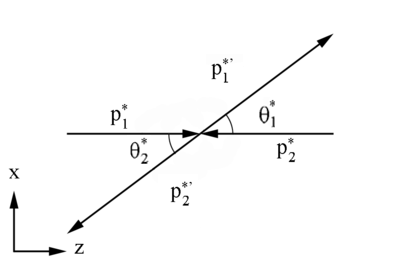
The t quantity is known as the square of the 4-momentum transfer | The t quantity is known as the square of the 4-momentum transfer | ||
| + | <center><math>t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2</math></center> | ||
| + | |||
| + | <center>[[File:400px-CMcopy.png]]</center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2</math></center> | ||
| + | |||
| + | |||
| + | <center><math>t \equiv P_1^{*2}-2P_1^*P_1^{'*}+P_1^{'*2}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>t \equiv 2m_1^2-2E_1^*E_1^{'*}+2p_1^*p_1^{'*}</math></center> | ||
| + | |||
| + | |||
| + | <center><math>t \equiv 2m_1^*-2E_1^{*2}+2p_1^{*2}cos\ \theta</math></center> | ||
| + | |||
| + | |||
| + | <center><math>t \equiv -2p_1^{*2}(1-cos\ \theta)</math></center> | ||
| + | |||
| + | ==u Channel== | ||
Revision as of 20:32, 8 June 2017
Mandelstam Representation

s Channel
The s quantity is known as the square of the center of mass energy (invariant mass)
As shown earlier, the square of a 4-momentum is
This gives
Similarly, the scalar product of two 4-momentums
In the center of mass frame of reference,
Using the relativistic energy equation
t Channel
The t quantity is known as the square of the 4-momentum transfer

u Channel