Difference between revisions of "Limits based on Mandelstam Variables"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
| − | <center><math>P^{2} \equiv m^2</math></center> | + | <center><math>\mathbf P^{2} \equiv m^2</math></center> |
| Line 22: | Line 22: | ||
| + | This gives | ||
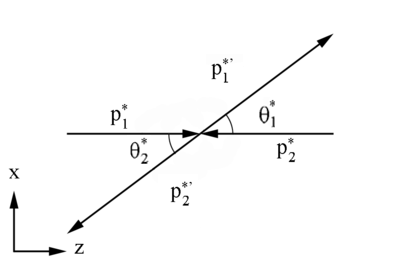
<center><math>s \equiv 2m^{2}+2 \mathbf P_1^* \mathbf P_2^*</math></center> | <center><math>s \equiv 2m^{2}+2 \mathbf P_1^* \mathbf P_2^*</math></center> | ||
| + | Similarly, the scalar product of two 4-momentums | ||
| + | <center><math>s \equiv 2m^2+2(E_1^*E_2^*-p_1^*p_2^*)</math></center> | ||
| + | |||
| + | |||
| + | In the center of mass frame of reference, | ||
| + | |||
| + | <center><math>E_1^*=E_2^* \quad \vec p_1^*=-\vec p_2^*</math></center> | ||
| + | |||
| + | |||
| + | <center><math>s \equiv 2m^2+2(E_1^*E_2^*-p_1^*p_2^*)</math></center> | ||
<center><math>s=4(m_{CM}^2+p_{CM}^2)</math></center> | <center><math>s=4(m_{CM}^2+p_{CM}^2)</math></center> | ||