|
|
| Line 35: |
Line 35: |
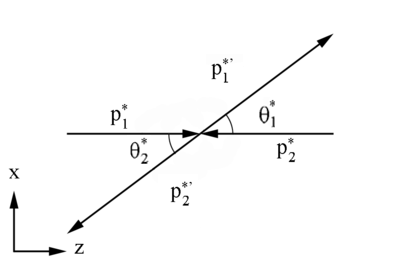
| | ==t Channel== | | ==t Channel== |
| | | | |
| − | <center><math>s \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2</math></center> | + | <center><math>t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2</math></center> |
| | | | |
| | <center>[[File:400px-CMcopy.png]]</center> | | <center>[[File:400px-CMcopy.png]]</center> |
| Line 41: |
Line 41: |
| | | | |
| | | | |
| − | <center><math>s \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2</math></center> | + | <center><math>t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2</math></center> |
| | | | |
| | | | |
| − | <center><math>s \equiv P_1^{*2}-2P_1^*P_1^{'*}+P_1^{'*2}</math></center> | + | <center><math>t \equiv P_1^{*2}-2P_1^*P_1^{'*}+P_1^{'*2}</math></center> |
| | | | |
| | | | |
| − | <center><math>s \equiv 2m_1^2-2E_1^*E_1^{'*}+2p_1^*p_1^{'*}</math></center> | + | <center><math>t \equiv 2m_1^2-2E_1^*E_1^{'*}+2p_1^*p_1^{'*}</math></center> |
| | | | |
| | | | |
| − | <center><math>s \equiv 2m_1^*-2E_1^{*2}+2p_1^{*2}cos \theta</math></center> | + | <center><math>t \equiv 2m_1^*-2E_1^{*2}+2p_1^{*2}cos\ \theta</math></center> |
| | | | |
| | | | |
| − | <center><math>s \equiv -2p_1^{*2}(1-cos \theta)</math></center> | + | <center><math>t \equiv -2p_1^{*2}(1-cos\ \theta)</math></center> |
| | | | |
| | ==u Channel== | | ==u Channel== |
Revision as of 16:41, 8 June 2017
Limits based on Mandelstam Variables
s Channel
[math]s \equiv \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=\left({\mathbf P_1^{'*}}+ {\mathbf P_2^{'*}}\right)^2[/math]
In the center of mass frame, the momentum of the particles interacting are equal and opposite, i.e. [math]p_1^*=-p_2^*[/math]. However, the 4-momentum still retains an energy component, which as a scalar quantity, can not be countered by another particle's direction of motion.
[math]{\mathbf P_1^*}\equiv \left(\begin{matrix} E_1\\ p_{x_1} \\ p_{y_1} \\ p_{z_1} \end{matrix} \right) \ \ \ \ {\mathbf P_2^*}\equiv \left(\begin{matrix} E_2\\ p_{x_2} \\ p_{y_2} \\ p_{z_2} \end{matrix} \right)[/math]
[math] \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=\left( \left(\begin{matrix} E_1\\ p_{x_1} \\ p_{y_1} \\ p_{z_1} \end{matrix} \right)+\left(\begin{matrix} E_2\\ p_{x_2} \\ p_{y_2} \\ p_{z_2} \end{matrix} \right) \right)^2[/math]
[math] \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=\left( \left(\begin{matrix} E_1\\ p_{x_1} \\ p_{y_1} \\ p_{z_1} \end{matrix} \right)+\left(\begin{matrix} E_2\\ -p_{x_1} \\ -p_{y_1} \\ -p_{z_1} \end{matrix} \right) \right)^2[/math]
[math] \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2= \left(\begin{matrix} E_1+E_2\\0 \\ 0 \\ 0 \end{matrix} \right)^2= \left(\begin{matrix}E_{CM}\\0 \\ 0 \\ 0 \end{matrix} \right)^2[/math]
Similarly, by the relativistic definition of energy
[math]E^2 \equiv p^2+m^2[/math]
where both particles have the same mass, this implies
[math] \left({\mathbf P_1^*}+ {\mathbf P_2^{*}}\right)^2=4E_{CM}^2=4(m_{CM}^2+p_{CM}^2)=s[/math]
[math]s=4(m_{CM}^2+p_{CM}^2)[/math]
t Channel
[math]t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2[/math]
[math]t \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2[/math]
[math]t \equiv P_1^{*2}-2P_1^*P_1^{'*}+P_1^{'*2}[/math]
[math]t \equiv 2m_1^2-2E_1^*E_1^{'*}+2p_1^*p_1^{'*}[/math]
[math]t \equiv 2m_1^*-2E_1^{*2}+2p_1^{*2}cos\ \theta[/math]
[math]t \equiv -2p_1^{*2}(1-cos\ \theta)[/math]
u Channel
