Difference between revisions of "Limits based on Mandelstam Variables"
Jump to navigation
Jump to search
| Line 37: | Line 37: | ||
<center><math>s \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2</math></center> | <center><math>s \equiv \left({\mathbf P_1^*}- {\mathbf P_1^{'*}}\right)^2=\left({\mathbf P_2^{*}}+ {\mathbf P_2^{'*}}\right)^2</math></center> | ||
| − | [[File:400px-CMcopy.png]] | + | <center>[[File:400px-CMcopy.png]]</center> |
| − | <center><math>{\mathbf P_1^*}\equiv \left(\begin{matrix} E_1\\ p_{x_1^*} \\ p_{y_1^*} \\ p_{z_1^*} \end{matrix} \right) \ \ \ \ {\mathbf P_1^{'*}}\equiv \left(\begin{matrix} E_1^{ | + | |
| + | <center><math>{\mathbf P_1^*}\equiv \left(\begin{matrix} E_1^*\\ p_{x_1^*} \\ p_{y_1^*} \\ p_{z_1^*} \end{matrix} \right) \ \ \ \ {\mathbf P_1^{'*}}\equiv \left(\begin{matrix} E_1^{'*}\\ p_{x_2^{'*}} \\ p_{y_2^{'*}} \\ p_{z_2^{'*}} \end{matrix} \right)</math></center> | ||
| + | |||
| + | |||
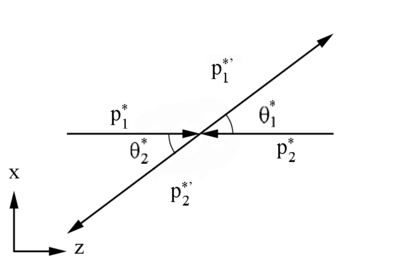
| + | The energy is conserved after the collision, | ||
| + | |||
| + | <center><math>E_1^*=E_1^{'*}</math></center> | ||
| + | |||
| + | |||
| + | The momentum is also conserved in the center of mass frame in magnitude, but not direction, | ||
| + | |||
| + | <center><math>|p_1^*|=|p_1^{'*}|</math></center> | ||
==u Channel== | ==u Channel== | ||
Revision as of 16:33, 8 June 2017
Limits based on Mandelstam Variables
s Channel
In the center of mass frame, the momentum of the particles interacting are equal and opposite, i.e. . However, the 4-momentum still retains an energy component, which as a scalar quantity, can not be countered by another particle's direction of motion.
Similarly, by the relativistic definition of energy
where both particles have the same mass, this implies
t Channel

The energy is conserved after the collision,
The momentum is also conserved in the center of mass frame in magnitude, but not direction,