Difference between revisions of "Relativistic Frames of Reference"
Jump to navigation
Jump to search
| Line 60: | Line 60: | ||
| − | <center><math> | + | <center><math>\frac{(\Delta x')^2+(\Delta y')^2+(\Delta z')^2}{(\Delta t')^2}= c^2=\frac{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}{(\Delta t)^2}</math></center> |
| + | |||
| + | This is possible since the ratios of distance to time are multiples of the same base, i.e. <math>\frac{3\times 10^8\ m}{s}</math> | ||
Revision as of 04:07, 3 June 2017
Relativistic Frames of Reference
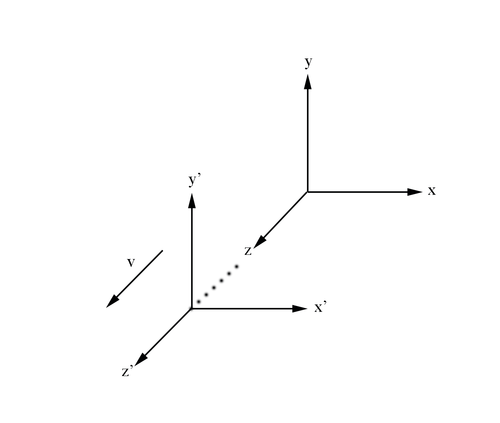
From the Galilean description of motion for a frame of reference moving relative to another frame considered stationary we know that
Using Einstein's Theory of Relativity, we know that the speed of light is a constant, c, for all reference frames. In the unprimed frame, from the definition of speed:
where
Using the distance equation in a Cartesian coordinate system, the equation for the speed of light becomes
Following the postulate of Special Relativity, this implies for the primed frame
We can rewrite this as
This is possible since the ratios of distance to time are multiples of the same base, i.e.