Difference between revisions of "Plotting Different Frames"

From New IAC Wiki
Jump to navigation Jump to search
Line 436: Line 436:
  
 
We can see that at the vertex position, the parameter reaches it's minimum at 1.4676.  This point reflects the right and left sides of the ellipse and the corresponding decreases in wire number as the parameter is increased.
 
We can see that at the vertex position, the parameter reaches it's minimum at 1.4676.  This point reflects the right and left sides of the ellipse and the corresponding decreases in wire number as the parameter is increased.
 +
 +
<pre>
 +
\[Theta] = 40;
 +
ellipse40full =
 +
  ContourPlot[(x + \[CapitalDelta]a)^2/a^2 + y^2/b^2 == 1, {y, -3,
 +
    3}, {x, -4, 1.8}, Frame -> {True, True, False, False},
 +
  PlotLabel ->
 +
    "X'/X'' & Y'Y'' position on DC sector plane as a function of \
 +
\[Phi] for \[Theta]=40\[Degree]",
 +
  FrameLabel -> {"y'/y'' (meters)", "x'/x'' (meters)"},
 +
  ContourStyle -> Red, PlotLegends -> Automatic];
 +
ellipse40Rotatedfull =
 +
  ContourPlot[(X Cos[6 \[Degree]] +
 +
      Y Sin[6 \[Degree]] + \[CapitalDelta]a)^2/
 +
    a^2 + (-X Sin[6 \[Degree]] + Y Cos[6 \[Degree]])^2/b^2 ==
 +
    1, {Y, -3, 3}, {X, -4, 1.8}, Frame -> {True, True, False, False},
 +
  PlotLabel ->
 +
    "X'' & Y'' position on DC sector wires a function of \[Phi] for \
 +
\[Theta]=40\[Degree]", FrameLabel -> {"y'' (meters)", "x'' (meters)"},
 +
    ContourStyle -> Blue, PlotLegends -> Automatic];
 +
SemiMajorAxisfull =
 +
  ContourPlot[Y == 0, {Y, -3, 3}, {X, -4, 1.8},
 +
  Frame -> {True, True, False, False},
 +
      PlotLabel ->
 +
    "Right side limit of DC as a function of X and Y",
 +
  FrameLabel -> {"y (meters)", "x (meters)"}, ContourStyle -> Red,
 +
      PlotLegends -> Automatic];
 +
SemiMajorAxisRotatedfull =
 +
  ContourPlot[X == 9.614 Y, {Y, -3, 3}, {X, 0 - 4, 1.8},
 +
  Frame -> {True, True, False, False},
 +
      PlotLabel ->
 +
    "Right side limit of DC as a function of X/X'' and Y",
 +
  FrameLabel -> {"y (meters)", "x (meters)"}, ContourStyle -> Blue,
 +
      PlotLegends -> Automatic];
 +
 +
 +
Show[ellipse40full, ellipse40Rotatedfull, SemiMajorAxisRotatedfull, \
 +
SemiMajorAxisfull]
 +
</pre>
 +
 +
 +
[[File:X1x2&y1y2ellipse.png]]

Revision as of 21:03, 3 May 2017

We can define different arrays to collect the coordinates in the different frames using a passive transformation. Assuming that the intersection of the ellipse and sense wires is in the y-x plane, we will have a positive rotation, [math]R(\theta_{yx})[/math] 


rFromYtoX = ( {
    {Cos[6 \[Degree]], -Sin[6 \[Degree]], 0},
    {Sin[6 \[Degree]], Cos[6 \[Degree]], 0},
    {0, 0, 1}
   } );
rFromXtoY = ( {
    {Cos[6 \[Degree]], Sin[6 \[Degree]], 0},
    {-Sin[6 \[Degree]], Cos[6 \[Degree]], 0},
    {0, 0, 1}
   } );
yxPoints = constant\[Theta];
constant\[Theta]yx = constant\[Theta];
constant\[Theta]yxRotated = constant\[Theta];
constant\[Theta]xyz = constant\[Theta];
constant\[Theta]xyzRotated = constant\[Theta];

RowLengths = Table[{Nothing}, {i, 1, 36}];
For[rows = 1, rows < 37, rows++,
  RowLengths[[rows]] = Length[constant\[Theta][[rows]]];
  For[columns = 1, columns < RowLengths[[rows]] + 1, columns++,
   \[Theta] = rows + 4;
   \[Phi] = constant\[Theta][[rows, columns, 1]];
   constant\[Theta]yx[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a};
   constant\[Theta]xyz[[rows, 
     columns]] = {constant\[Theta]yx[[rows, columns, 2]], 
     constant\[Theta]yx[[rows, columns, 1]], 0};
   If[constant\[Theta][[rows, columns, 1]] < 0,
    constant\[Theta]yx[[rows, columns, 
      1]] = -constant\[Theta]yx[[rows, columns, 1]];
    constant\[Theta]xyz[[rows, columns, 
      2]] = -constant\[Theta]xyz[[rows, columns, 2]];
    ];
   constant\[Theta]xyzRotated[[rows, columns]] = 
    rFromYtoX.{constant\[Theta]xyz[[rows, columns, 1]], 
      constant\[Theta]xyz[[rows, columns, 2]], 
      constant\[Theta]xyz[[rows, columns, 3]]};
   
   constant\[Theta]yxRotated[[rows, 
     columns]] = {constant\[Theta]xyzRotated[[rows, columns, 2]], 
     constant\[Theta]xyzRotated[[rows, columns, 1]]};
   yxPoints[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a, 
     constant\[Theta][[rows, columns, 1]], 
     constant\[Theta][[rows, columns, 2]]};
   
   ]
  ];
ClearAll[\[Theta], \[Phi]];
DesiredyxPoints = Desiredconstant\[Theta];
Desiredconstant\[Theta]yx = Desiredconstant\[Theta];
Desiredconstant\[Theta]yxRotated = Desiredconstant\[Theta];
Desiredconstant\[Theta]xyz = Desiredconstant\[Theta];
Desiredconstant\[Theta]xyzRotated = Desiredconstant\[Theta];

DesiredRowLengths = Table[{Nothing}, {i, 1, 36}];
For[rows = 1, rows < 37, rows++,
  DesiredRowLengths[[rows]] = 
   Length[Desiredconstant\[Theta][[rows]]];
  For[columns = 1, columns < DesiredRowLengths[[rows]] + 1, 
   columns++,
   \[Theta] = rows + 4;
   \[Phi] = Desiredconstant\[Theta][[rows, columns, 1]];
   Desiredconstant\[Theta]yx[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a};
   Desiredconstant\[Theta]xyz[[rows, 
      columns]] = {Desiredconstant\[Theta]yx[[rows, columns, 2]], 
     Desiredconstant\[Theta]yx[[rows, columns, 1]], 0};
   If[Desiredconstant\[Theta][[rows, columns, 1]] < 0,
    Desiredconstant\[Theta]yx[[rows, columns, 
       1]] = -Desiredconstant\[Theta]yx[[rows, columns, 1]];
    Desiredconstant\[Theta]xyz[[rows, columns, 
       2]] = -Desiredconstant\[Theta]xyz[[rows, columns, 2]];
    ];
   Desiredconstant\[Theta]xyzRotated[[rows, columns]] = 
    rFromYtoX.{Desiredconstant\[Theta]xyz[[rows, columns, 1]], 
      Desiredconstant\[Theta]xyz[[rows, columns, 2]], 
      Desiredconstant\[Theta]xyz[[rows, columns, 3]]};
   
   Desiredconstant\[Theta]yxRotated[[rows, 
      columns]] = {Desiredconstant\[Theta]xyzRotated[[rows, columns, 
       2]], Desiredconstant\[Theta]xyzRotated[[rows, columns, 1]]};
   DesiredyxPoints[[rows, columns]] = {y, 
     Sqrt[a^2 (1 - y^2/b^2)] - \[CapitalDelta]a, 
     Desiredconstant\[Theta][[rows, columns, 1]], 
     Desiredconstant\[Theta][[rows, columns, 2]]};
   
   ]
  ];
ClearAll[\[Theta], \[Phi]]


The parameter's range changes from the DC frame with 0<t<2[math]\pi[/math], since

[math]x(t=0)=a\ cos\ t = a\ cos\ 0 =a = a\ cos\ 2 \pi =x(t=2 \pi)[/math]


[math]y(t=0)=b\ sin\ t = b\ sin\ 0 = 0 = b\ sin\ 2 \pi = y(t=2 \pi)[/math]

In the frame of the wires, the x axis no longer is aligned with the semi-major axis, therefore for [math]\theta=40^{\circ}, \phi=0, t=0 [/math] in the DC frame 


In[153]:= ClearAll[X, \[Theta]];
\[Theta] = 40;
X = X /. Solve[(X + \[CapitalDelta]a)^2/a^2 == 1 && X > 0, X]

Out[155]= {1.68318}

This gives the (x' , y')=(1.68318, 0) in the DC frame for[math] \phi=0^{\circ}, t=0[/math]


The center of the ellipse in the DC frame becomes 

In[157]:= rFromYtoX.{\[CapitalDelta]a, 0, 0} // MatrixForm

Out[157]//MatrixForm= \!\(
TagBox[
RowBox[{"(", "", 
TagBox[GridBox[{
{"1.0760024073650314`"},
{"0.11309241017012851`"},
{"0.`"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.5599999999999999]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}}],
Column], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)


Likewise the position where the semi-major axis is reached on the x' axis becomes 

In[158]:= rFromYtoX.{1.6831832367824053`, 0, 0} // MatrixForm

Out[158]//MatrixForm= \!\(
TagBox[
RowBox[{"(", "", 
TagBox[GridBox[{
{"1.6739625828969429`"},
{"0.17594055713873974`"},
{"0.`"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.5599999999999999]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}}],
Column], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)


The slope m, with respect to x, is found as[math]\frac{ \Delta x}{\Delta y} = \frac{(1.67396 - 1.076)}{(0.175941 - 0.113092)}=\frac{0.59796}{0.0628481}[/math]=9.514


Slope point form gives

[math]x-x_1=m(y-y_1) [/math]
[math]\Rightarrow x - 1.67396 = 9.514(y - 0.17594) [/math]
[math]\Rightarrow y = 9.514x-1.67396 + 1.67396[/math]
[math]\Rightarrow y = 9.514x[/math]


SemiMajorAxis = 
  ContourPlot[Y == 0, {Y, -1, 1}, {X, 0, 1.8}, 
   Frame -> {True, True, False, False}, 
       PlotLabel -> 
    "Right side limit of DC as a function of X and Y", 
   FrameLabel -> {"y (meters)", "x (meters)"}, ContourStyle -> Red, 
       PlotLegends -> Automatic];
SemiMajorAxisRotated = 
  ContourPlot[X == 9.614 Y, {Y, -2, 2}, {X, 0, 1.8}, 
   Frame -> {True, True, False, False}, 
       PlotLabel -> 
    "Right side limit of DC as a function of X and Y", 
   FrameLabel -> {"y (meters)", "x (meters)"}, ContourStyle -> Blue, 
       PlotLegends -> Automatic];

The center 


In[161]:= rFromXtoY.{\[CapitalDelta]a, 0, 0} // MatrixForm

Out[161]//MatrixForm= \!\(
TagBox[
RowBox[{"(", "", 
TagBox[GridBox[{
{"1.0760024073650314`"},
{
RowBox[{"-", "0.11309241017012851`"}]},
{"0.`"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.5599999999999999]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}}],
Column], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)

The vertex 

In[162]:= rFromXtoY.{1.6831832367824053`, 0, 0} // MatrixForm

Out[162]//MatrixForm= \!\(
TagBox[
RowBox[{"(", "", 
TagBox[GridBox[{
{"1.6739625828969429`"},
{
RowBox[{"-", "0.17594055713873974`"}]},
{"0.`"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.5599999999999999]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}}],
Column], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)


The slope m, with respect to x, is found as [math]\frac{\Delta\ x}{\Delta\ y} = \frac{1.67396 - 1.076}{-0.175941 + 0.113092}=\frac{0.59796}{-0.0628481}=-9.514[/math]


Slope point form gives

[math]x' - x_1=m(y'-y_1) [/math]


[math]\Rightarrow x' - 1.67396 = -9.514(y' + 0.17594) [/math]


[math]\Rightarrow y' = 9.514x'-1.67396 + 1.67396[/math]


[math]\Rightarrow y' = -9.514x'[/math]



SemiMajorAxisRotatedReverse = 
  ContourPlot[X == -9.514 Y, {Y, -2, 2}, {X, 0, 1.8}, 
   Frame -> {True, True, False, False}, 
       PlotLabel -> 
    "Right side limit of DC as a function of X and Y", 
   FrameLabel -> {"y (meters)", "x (meters)"}, 
   ContourStyle -> Green, 
       PlotLegends -> Automatic];

Graphing the frame of the sector and the wires within the sector, 


DataXY = Table[
   ListPlot[{constant\[Theta]yx[[i]]}, PlotStyle -> Black, 
    AxesLabel -> {"y", "x"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"], {i, 1, 
    36}];
DataXYRotated = 
  Table[ListPlot[{constant\[Theta]yxRotated[[i]]}, PlotStyle -> Black,
     AxesLabel -> {"y'", "x'"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"],
   {i, 1, 36}];
DesiredDataXY = 
  Table[ListPlot[{Desiredconstant\[Theta]yx[[i]]}, PlotStyle -> Black,
     AxesLabel -> {"y", "x"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"], {i, 1, 
    36}];
DesiredDataXYRotated = 
  Table[ListPlot[{Desiredconstant\[Theta]yxRotated[[i]]}, 
    PlotStyle -> Black, AxesLabel -> {"y'", "x'"}, 
    PlotLabel -> 
     "DC Wire for Constant \[Theta] as a Function of \[Phi]"],
   {i, 1, 36}];
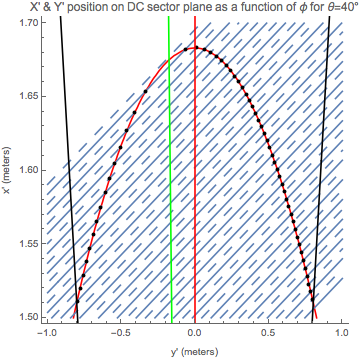
ClearAll[\[Theta]];
\[Theta] = 40;
ellipse40 = 
  ContourPlot[(x + \[CapitalDelta]a)^2/a^2 + y^2/b^2 == 1, {y, -1, 
    1}, {x, 1.5, 1.7}, Frame -> {True, True, False, False}, 
   PlotLabel -> 
    "X' & Y' position on DC sector plane as a function of \[Phi] for \
\[Theta]=40\[Degree]", FrameLabel -> {"y' (meters)", "x' (meters)"}, 
   ContourStyle -> Red, PlotLegends -> Automatic];
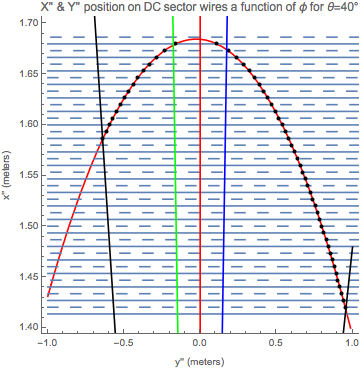
ellipse40Rotated = 
  ContourPlot[(X Cos[6 \[Degree]] + 
       Y Sin[6 \[Degree]] + \[CapitalDelta]a)^2/
     a^2 + (-X Sin[6 \[Degree]] + Y Cos[6 \[Degree]])^2/b^2 == 
    1, {Y, -1, 1}, {X, 1.4, 1.7}, Frame -> {True, True, False, False},
    PlotLabel -> 
    "X'' & Y'' position on DC sector wires a function of \[Phi] for \
\[Theta]=40\[Degree]", FrameLabel -> {"y'' (meters)", "x'' (meters)"},
    ContourStyle -> Red, PlotLegends -> Automatic];
Show[ellipse40, 
 Table[ContourPlot[
   xWire == Tan[6 \[Degree]] yWire + x0forWires[number], {yWire, -1, 
    1}, {xWire, 1.5, 1.7}, 
   FrameLabel -> {"y(meters)", "x(meters)"}], {number, 89, 109}], 
 Table[ContourPlot[
   xWire == 
    Tan[6 \[Degree]] yWire + x0forWireMiddles[number2], {yWire, -1, 
    1}, {xWire, 1.5, 1.7},
   ContourStyle -> {Dashing[Large]}], {number2, 89, 109}], 
 DataXY[[36]], 
 DesiredDataXY[[36]], left, right, SemiMajorAxis, \
SemiMajorAxisRotatedReverse]
Show[ellipse40Rotated, 
 Table[ContourPlot[
   xWire == Cos[6 \[Degree]] x0forWires[number], {yWire, -1, 
    1.2}, {xWire, 1.4, 1.7}, 
   FrameLabel -> {"y(meters)", "x(meters)"}], {number, 89, 109}], 
 Table[ContourPlot[
   xWire == Cos[6 \[Degree]] x0forWireMiddles[number2], {yWire, -1, 
    1.2}, {xWire, 1.4, 1.7},
   ContourStyle -> {Dashing[Large]}], {number2, 89, 109}], 
 DataXYRotated[[36]], 
 DesiredDataXYRotated[[36]], rightRotated, leftRotated, \
SemiMajorAxisRotated, SemiMajorAxis, SemiMajorAxisRotatedReverse]
ClearAll[\[Theta]];


X'y'plane.png


X2y2plane.png


The point that was the semi-major vertex, when rotated 6\[Degree] to the right becomes 

In[1603]:= rFromYtoX.{1.6831832367824053`, 0, 0} // MatrixForm

Out[1603]//MatrixForm= \!\(
TagBox[
RowBox[{"(", "", 
TagBox[GridBox[{
{"1.6739625828969429`"},
{"0.17594055713873974`"},
{"0.`"}
},
GridBoxAlignment->{
       "Columns" -> {{Center}}, "ColumnsIndexed" -> {}, 
        "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.5599999999999999]}, 
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]}, 
Offset[0.2]}, "RowsIndexed" -> {}}],
Column], "", ")"}],
Function[BoxForm`e$, 
MatrixForm[BoxForm`e$]]]\)


Solving for the ellipse parameter given the angle and the corresponding X and Y components 


X = 1.6739625828969429`;
Y = 0.17594055713873974`;
\[Theta] = 40;
t = t /. Solve[
   X^2 (Cos[6 \[Degree]])^2 + 
     Y^2 (Sin[6 \[Degree]])^2 + \[CapitalDelta]a^2 + 
     2 X Y Cos[6 \[Degree]] Sin[6 \[Degree]] + 
     2 X \[CapitalDelta]a Cos[6 \[Degree]] + 
     2 Y \[CapitalDelta]a Sin[6 \[Degree]] + 
     X^2 (Sin[6 \[Degree]])^2 + Y^2 (Cos[6 \[Degree]])^2 - 
     2 X Y Sin[6 \[Degree]] Cos[6 \[Degree]] == 
    a^2 (Cos[t])^2 (Cos[6 \[Degree]])^2 + 
     b^2 (Sin[t])^2 (Sin[6 \[Degree]])^2 + \[CapitalDelta]a^2 + 
     2 a b Cos[t] Cos[6 \[Degree]] Sin[t] Sin[6 \[Degree]] + 
     2 a \[CapitalDelta]a Cos[t] Cos[6 \[Degree]] + 
     2 b \[CapitalDelta]a Sin[t] Sin[6 \[Degree]] + 
     a^2 (Cos[t])^2 (Sin[6 \[Degree]])^2 + 
     b^2 (Sin[t])^2 (Cos[6 \[Degree]])^2 - 
     2 a b Cos[t] Sin[6 \[Degree]] Cos[6 \[Degree]] Sin[t], t]
ClearAll[X, Y, \[Theta]];



{-1.31406, 1.4676, 3.06482 - 1.66742 I, 3.06482 + 1.66742 I}

We can see that at the vertex position, the parameter reaches it's minimum at 1.4676. This point reflects the right and left sides of the ellipse and the corresponding decreases in wire number as the parameter is increased. 

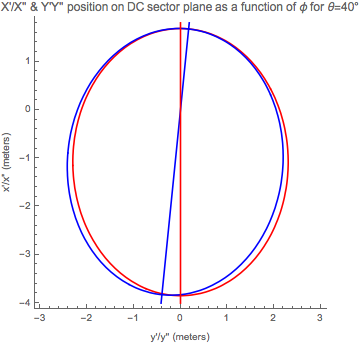
\[Theta] = 40;
ellipse40full = 
  ContourPlot[(x + \[CapitalDelta]a)^2/a^2 + y^2/b^2 == 1, {y, -3, 
    3}, {x, -4, 1.8}, Frame -> {True, True, False, False}, 
   PlotLabel -> 
    "X'/X'' & Y'Y'' position on DC sector plane as a function of \
\[Phi] for \[Theta]=40\[Degree]", 
   FrameLabel -> {"y'/y'' (meters)", "x'/x'' (meters)"}, 
   ContourStyle -> Red, PlotLegends -> Automatic];
ellipse40Rotatedfull = 
  ContourPlot[(X Cos[6 \[Degree]] + 
       Y Sin[6 \[Degree]] + \[CapitalDelta]a)^2/
     a^2 + (-X Sin[6 \[Degree]] + Y Cos[6 \[Degree]])^2/b^2 == 
    1, {Y, -3, 3}, {X, -4, 1.8}, Frame -> {True, True, False, False}, 
   PlotLabel -> 
    "X'' & Y'' position on DC sector wires a function of \[Phi] for \
\[Theta]=40\[Degree]", FrameLabel -> {"y'' (meters)", "x'' (meters)"},
    ContourStyle -> Blue, PlotLegends -> Automatic];
SemiMajorAxisfull = 
  ContourPlot[Y == 0, {Y, -3, 3}, {X, -4, 1.8}, 
   Frame -> {True, True, False, False}, 
       PlotLabel -> 
    "Right side limit of DC as a function of X and Y", 
   FrameLabel -> {"y (meters)", "x (meters)"}, ContourStyle -> Red, 
       PlotLegends -> Automatic];
SemiMajorAxisRotatedfull = 
  ContourPlot[X == 9.614 Y, {Y, -3, 3}, {X, 0 - 4, 1.8}, 
   Frame -> {True, True, False, False}, 
       PlotLabel -> 
    "Right side limit of DC as a function of X/X'' and Y", 
   FrameLabel -> {"y (meters)", "x (meters)"}, ContourStyle -> Blue, 
       PlotLegends -> Automatic];


Show[ellipse40full, ellipse40Rotatedfull, SemiMajorAxisRotatedfull, \
SemiMajorAxisfull]


X1x2&y1y2ellipse.png

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Plotting_Different_Frames&oldid=114296"