Difference between revisions of "GEANT Moller Simulations Comparison"
| Line 34: | Line 34: | ||
<center>[[File:MollerThetaLab_4e7_LH2_11GeV_Detector.png]][[File:MolThetaLab4e8LH211GeVDetector.png]]</center> | <center>[[File:MollerThetaLab_4e7_LH2_11GeV_Detector.png]][[File:MolThetaLab4e8LH211GeVDetector.png]]</center> | ||
| − | + | For 4e7 incident electrons: | |
<center><math>\sigma = \frac{N_{events}}{N_{incident}\ \rho\ \ell}=\frac{975593}{40000000\ \cdot 4.2\times 10^{-2} barns^{-1}}=\frac{0.024}{4.2\times 10^{-2} barns^{-1}}=0.58 barns</math></center> | <center><math>\sigma = \frac{N_{events}}{N_{incident}\ \rho\ \ell}=\frac{975593}{40000000\ \cdot 4.2\times 10^{-2} barns^{-1}}=\frac{0.024}{4.2\times 10^{-2} barns^{-1}}=0.58 barns</math></center> | ||
| Line 49: | Line 49: | ||
<center><math>\mathcal{L} \cdot t_{simulated}=\frac{N_{events}}{\sigma}</math></center> | <center><math>\mathcal{L} \cdot t_{simulated}=\frac{N_{events}}{\sigma}</math></center> | ||
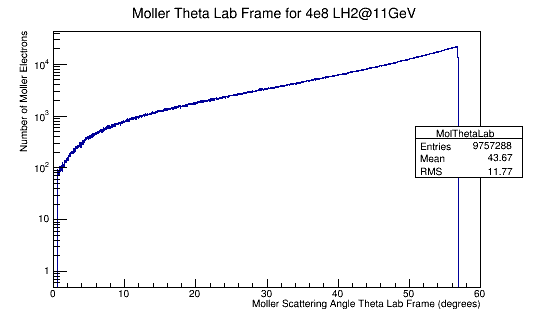
| + | For 4e8 incident electrons: | ||
| + | <center><math>\sigma = \frac{N_{events}}{N_{incident}\ \rho\ \ell}=\frac{9757288}{400000000\ \cdot 4.2\times 10^{-2} barns^{-1}}=\frac{0.024}{4.2\times 10^{-2} barns^{-1}}=0.58 barns</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\sigma=\frac{R_{events}}{\mathcal{L}} \Rightarrow \mathcal{L}=\frac{R_{events}}{\sigma}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\mathcal{L}=\frac{dN_{events}}{dt}\frac{1}{ \sigma}\Rightarrow \int_{0}^{t_{simulated}}\mathcal {L}\, dt= \int_{0}^{N_{events}}\frac{1}{\sigma}\, dN</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | <center><math>\mathcal{L} \cdot t_{simulated}=\frac{N_{events}}{\sigma}</math></center> | ||
For a Luminosity of <math>\mathcal{L}=\frac{1.3\times 10^{11}}{barn\cdot s}</math> | For a Luminosity of <math>\mathcal{L}=\frac{1.3\times 10^{11}}{barn\cdot s}</math> | ||
Revision as of 20:03, 1 January 2017
https://wiki.iac.isu.edu/index.php/Converting_to_barns
https://wiki.iac.isu.edu/index.php/Check_Differential_Cross-Section
Converting the number of electrons scattered per angle theta to barns, we can use the relation
If the time is taken to be the same for the amount scattered as for the amount incident (the time simulated), this can be viewed as the probability of one incident electron producing a Moller event.
While this expression has no explicit dependancies on energy, the ratio is a function of the energy, as well as the physical makeup of the target.
This gives, for LH2:
From earlier simulations for random angle Phi, we know that the full range of Theta is limited depending on the target material.
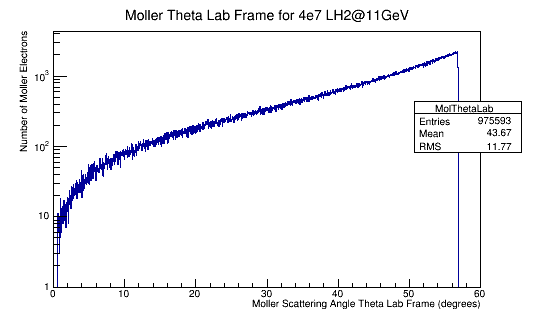
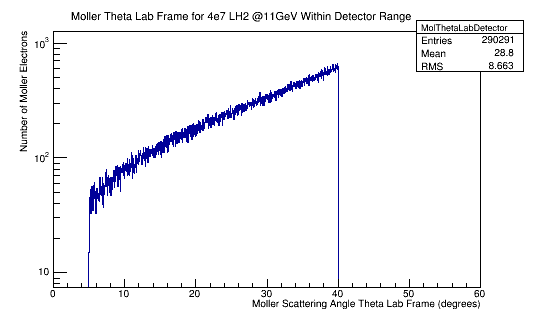
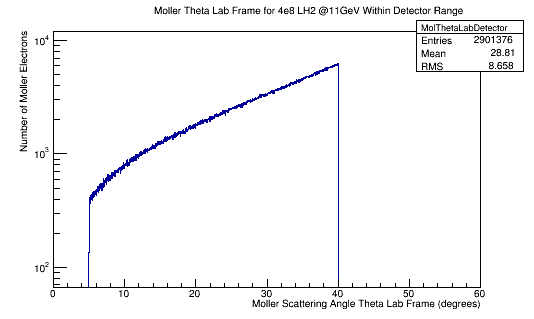
For 4e7 incident electrons:
For 4e8 incident electrons:
For a Luminosity of